并查集（21.7.20）

Posted 2021-08-19 未定_

一.并查集:一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。
通俗一点，就像是不同的帮派，每个帮派有一个大首领，大首领底下又有一些小首领，每个小首领底下有一群小兵，这些人都属于一个帮派也就是同一个根。并查集就是处理派与派，首领与小兵，小兵与小兵等之间的关系问题。
二.简单实现:
这里通过数组实现，即s[x]=i，x表示小兵，i表示小兵的首领，每个小兵都间接属于首领的首领，也就是整个派系有一个大首领，派系的所有人都直接或间接属于这个大首领。
•初始化：数组标号表示不同的人，初始时所有人都没有划分派系
•查询：以下有两种方式
路径未压缩 return x==s[x]?x:find_set(s[x])

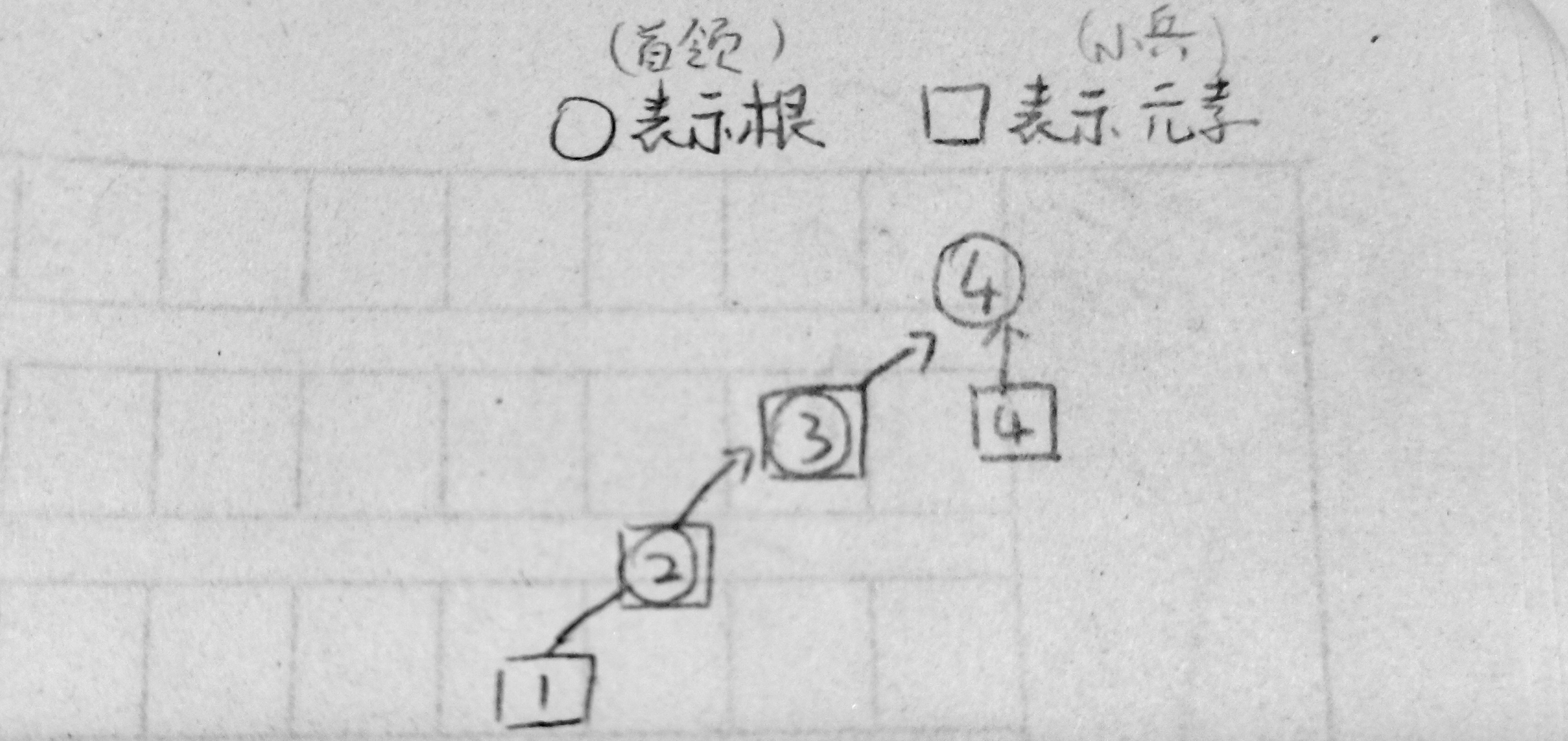
路径压缩 return s[x]==x?x:s[x]=find_set(s[x]);

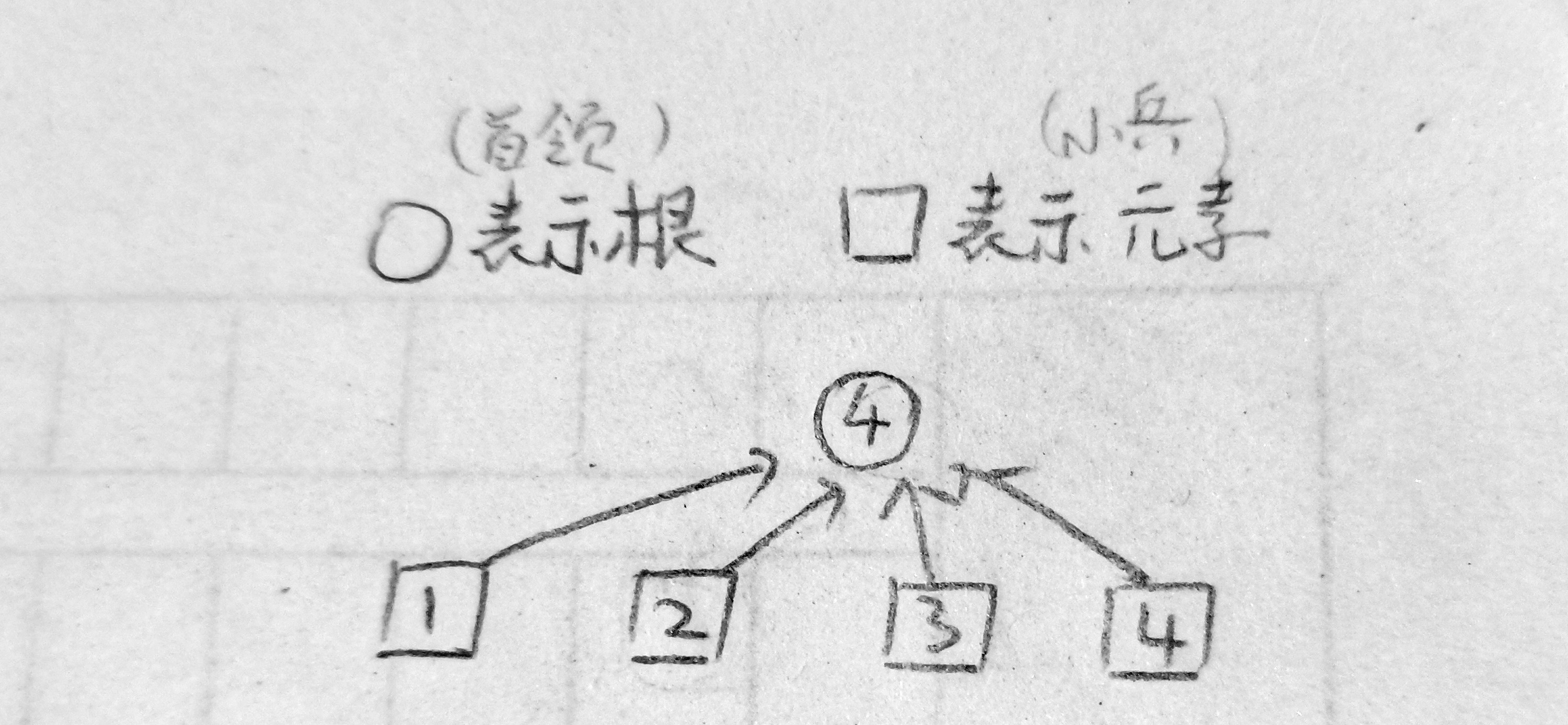
•合并：同一个首领的人合并在一起从属于同一个首领，同一个派的人合并在一起，属于一个派。
三.常见题型模板
•维护相同集合： 告诉你a，b在同一派
例：Ubiquitous Religions
模板1：

const int maxn=50000;
int s[maxn+1];
void init_set()//初始化
{
    for(int i=0; i<=maxn; i++)
    {
        s[i]=i;
    }
}
int find_set(int x)//查询
{
    return x==s[x]?x:find_set(s[x]);//递归找根，数组的值代表根
}
void union_set(int x,int y)//合并
{
    x=find_set(x);
    y=find_set(y);
    if(x!=y)s[x]=s[y];//让y和x同一个根，即都是y的根
}

模板2（更优化）：

int s[maxn+1];
int h[maxn+1];
void init_set()//初始化
{
    for(int i=0; i<=maxn; i++)
    {
        s[i]=i;
        h[i]=0;//树的高度
    }
}
int find_set(int x)//查询，路径压缩，即让派里的所以人都直接从属于一个首领，首领就是根结点
{
    int r=x;
    while(s[r]!=r) r=s[r];//找到根结点
    int i=x,j;
    while(i!=r)
    {
        j=s[i];
        s[i]=r;//把路径上元素的集改成根结点
        i=j;
    }
    return r;
}
void union_set(int x,int y)//合并
{
    x=find_set(x);
    y=find_set(y);
    if(h[x]==h[y])
    {
        h[x]=h[x]+1;//合并，树的高度加1
        s[y]=x;
    }
    else
    {
        if(h[x]<h[y])//把矮树并到高树上，高树的高度保持不变
            s[x]=y;
        else s[y]=x;
    }
}

•维护不同集合：告诉你a，b在不同派
例：Find them, Catch them
原理：unite_set(a,b)表示a,b属于同一个集合，现在用unite_set(a,b+n)来表示a,b属于不同集合，即a属于第一个集合，b属于第二个集合。同理unite(a+n,b)表示a属于第二个集合 b属于第一个集合。
局限：以下代码仅限于两个派的情况，即如果知道了a与b是不同集合，b与c是不同集合，也就知道了c与a是同一集合。
模板1：

const int maxn=1e5+5;
int s[maxn*2];
int h[maxn*2];
void init_set()//初始化
{
    for(int i=0; i<=2*maxn; i++)
    {
        s[i]=i;
        h[i]=0;
    }
}
int find_set(int x)//查询，路径未压缩
{
    return x==s[x]?x:find_set(s[x]);//返回根结点
}
void union_set(int x,int y)//合并
{
    x=find_set(x);
    y=find_set(y);
    if(x==y)
        return;
    if(h[x]==h[y])
    {
        h[x]=h[x]++;
        s[y]=x;
    }
    else
    {
        if(h[x]<h[y])
            s[x]=y;
        else s[y]=x;
    }
}
bool same (int x,int y)
{
    return find_set(x)==find_set(y);
}

模板2：与模板1的查询和合并函数不同

const int maxn=1e5+5;
int s[maxn*2];
int h[maxn*2];
void init_set()//初始化
{
    for(int i=0; i<=2*maxn; i++)
    {
        s[i]=i;
        h[i]=0;
    }
}
int find_set(int x)//查询，路径压缩
{
    return s[x]==x?x:s[x]=find_set(s[x]);//每个小兵都直接从属于首领了
}
void union_set(int x,int y)//合并
{
    x=find_set(x);
    y=find_set(y);
    if(x==y)
        return;
    if(h[x]<h[y])
    {
        s[x]=y;
    }
    else
    {
        s[y]=x;
        if(h[x]==h[y])
            h[x]++;
    }
}
bool same (int x,int y)
{
    return find_set(x)==find_set(y);
}

注意：法1与法2的查询函数与合并函数只能这样匹配，不能混用，否则会出错。
•求某一个派（集合）的人数
例：The Suspects

int s[maxn+1];
int z[maxn+1];//用来记录某派人数
void init_set()//初始化
{
    for(int i=0; i<=maxn; i++)
    {
        s[i]=i;
        z[i]=1;
    }
}
int find_set(int x)//查询
{
    return s[x]==x?s[x]:s[x]=find_set(s[x]);
}
void union_set(int x,int y)//合并
{
    x=find_set(x);
    y=find_set(y);
    if(x!=y)
    {s[x]=y;
    z[y]+=z[x];
    }
}

求某派（派名：根结点）的人数：
cout<<z[find_set(根节点)]<<endl;