377. 组合总和 Ⅳ（背包dp）

Posted 2021-08-18 mp-ui

377. 组合总和 Ⅳ

题目描述

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

 

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。
示例 2：

输入：nums = [9], target = 3
输出：0
 

提示：

1 <= nums.length <= 200
1 <= nums[i] <= 1000
nums 中的所有元素 互不相同
1 <= target <= 1000
 

进阶：如果给定的数组中含有负数会发生什么？问题会产生何种变化？如果允许负数出现，需要向题目中添加哪些限制条件？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combination-sum-iv
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

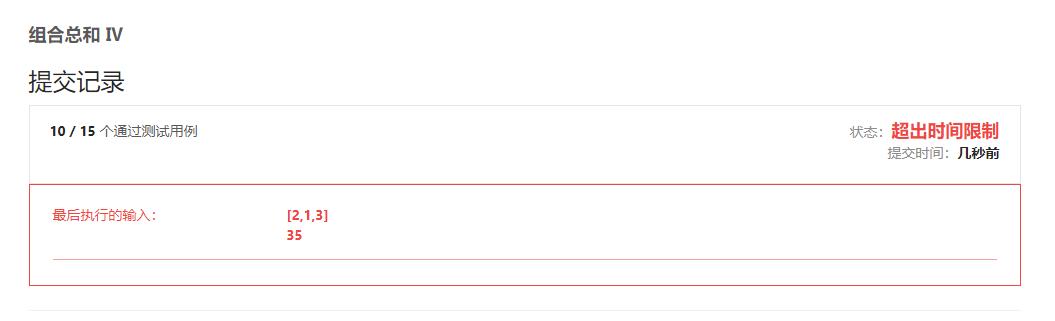
解法1：暴力dfs（超时）

暴力DFS，没啥好说的，卡在第10个样例

代码如下：

class Solution {
    int cnt = 0;

    public int combinationSum4(int[] nums, int target) {
        Arrays.sort(nums);
        dfs(nums,target);
        return cnt;
    }

    public void dfs(int[] nums,int target){
        if(target == 0){
            ++cnt;
            return;
        }
        if(target < 0){
            return;
        }
        for (int num : nums) {
            dfs(nums,target - num);
        }
    }

}

运行结果：

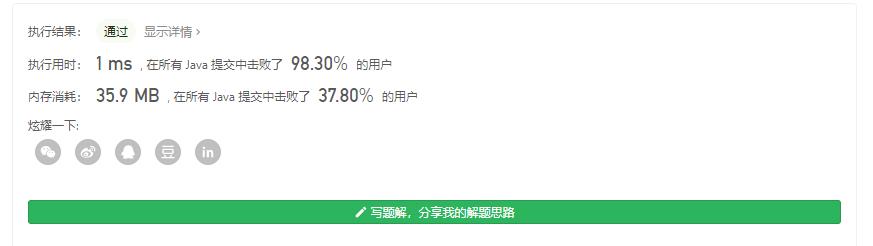
解法2：记忆化递归

这也没啥好说的，有手就行

代码如下：

class Solution {
    int[] dp;

    public int combinationSum4(int[] nums, int target) {
        dp = new int[target + 1];
        Arrays.fill(dp,-1);
        Arrays.sort(nums);
        return dfs(nums,target);
    }

    public int dfs(int[] nums,int target){
        if(target == 0){
            return 1;
        }
        if(target < 0){
            return 0;
        }
        if(dp[target] >= 0){
            return dp[target];
        }
        int res = 0;
        for (int num : nums) {
            res += dfs(nums,target - num);
        }
        dp[target] = res;
        return res;
    }
}

运行结果：

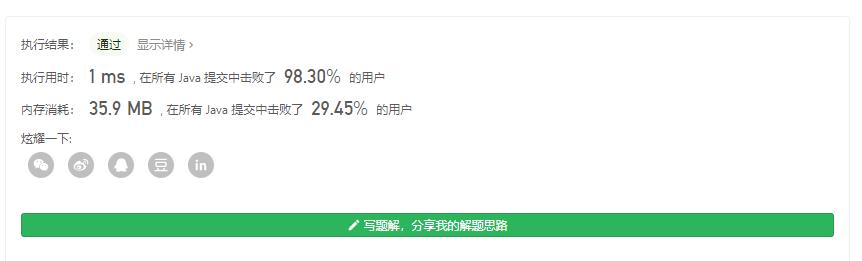
解法3：动态规划（背包问题）

一般能通过记忆化递归做的题目都可以通过动态规划，因为这两个是反着来的，动态规划是从前往后推，而记忆化计划是从后往前推。

代码如下：

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];  //dp[i]:nums中元素总和为i的组合的个数
        dp[0] = 1;  //组成0的情况有1种，就是什么都不选
        for (int i = 1; i <= target; i++) {
            for (int num : nums) {
                if(i - num >= 0){
                    dp[i] += dp[i - num];
                }
            }
        }
        return dp[target];
    }
}

运行结果：