363. 矩形区域不超过 K 的最大数值和（状态压缩dp）

Posted 2021-08-18 mp-ui

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了363. 矩形区域不超过 K 的最大数值和（状态压缩dp）相关的知识，希望对你有一定的参考价值。

363. 矩形区域不超过 K 的最大数值和

题目描述

363. 矩形区域不超过 K 的最大数值和
给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。

题目数据保证总会存在一个数值和不超过 k 的矩形区域。

 

示例 1：


输入：matrix = [[1,0,1],[0,-2,3]], k = 2
输出：2
解释：蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。
示例 2：

输入：matrix = [[2,2,-1]], k = 3
输出：3
 

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
-105 <= k <= 105
 

进阶：如果行数远大于列数，该如何设计解决方案？

请添加图片描述

解法1：普通dp+暴力

class Solution {
    public int maxSumSubmatrix(int[][] matrix, int k) {
        int res = Integer.MIN_VALUE;
        int m = matrix.length;
        int n = matrix[0].length;
        int[][][][] dp = new int[m][n][m][n];
        //dp[a][b][c][d]:矩形左上角(a,b)，右下角(c,d)的和
        for (int i1 = 0; i1 < m; i1++) {
            for (int j1 = 0; j1 < n; j1++) {
                if(matrix[i1][j1] > res && matrix[i1][j1] <= k){
                    res = matrix[i1][j1];
                }
                dp[i1][j1][i1][j1] = matrix[i1][j1]; // 左上角和右下角都是同一个点的矩形，就是一个点。
                //(i1,j1)右边的那一行
                for (int j2 = j1 + 1; j2 < n; j2++) {
                    dp[i1][j1][i1][j2] = dp[i1][j1][i1][j2 - 1] + matrix[i1][j2];
                    //判断
                    if(dp[i1][j1][i1][j2] > res && dp[i1][j1][i1][j2] <= k){
                        res = dp[i1][j1][i1][j2];
                    }
                }
                //(i1,j1)下边的那一竖
                for (int i2 = i1 + 1; i2 < m; i2++) {
                    dp[i1][j1][i2][j1] = dp[i1][j1][i2-1][j1] + matrix[i2][j1];
                    //判断
                    if(dp[i1][j1][i2][j1] > res && dp[i1][j1][i2][j1] <= k){
                        res = dp[i1][j1][i2][j1];
                    }
                }
                //(i1,j1)右下方
                for (int i2 = i1 + 1; i2 < m; i2++) {
                    for (int j2 = j1 + 1; j2 < n; j2++) {
                        dp[i1][j1][i2][j2] = dp[i1][j1][i2-1][j2] + dp[i1][j1][i2][j2-1] - dp[i1][j1][i2-1][j2-1] + matrix[i2][j2];
                        //判断
                        if(dp[i1][j1][i2][j2] > res && dp[i1][j1][i2][j2] <= k){
                            res = dp[i1][j1][i2][j2];
                        }
                    }
                }
            }
        }
        return res;
    }
}

时间复杂度：O(m^2 n^2)

空间复杂度：O(m^2 n^2)

运行结果：

请添加图片描述

解法2：在解法1的基础上进行状态压缩

通过解法1的代码可以发现，在第二层循环里面（dp数组的前两个维的值永远是i1,j1），取其他值的情况我们在循环里面都没用上，所有我们可以干脆把数组从4维降到二维。

令dp[i2][j2]代表矩形左上角(i1,j1)，右下角(i2,j2)，这个矩形里面所有元素的和

所以改写代码如下：

class Solution {
    public int maxSumSubmatrix(int[][] matrix, int k) {
        int res = Integer.MIN_VALUE;
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] dp = new int[m][n];
        //令`dp[i2][j2]`代表矩形左上角(i1,j1)，右下角(i2,j2)，这个矩形里面所有元素的和
        for (int i1 = 0; i1 < m; i1++) {
            for (int j1 = 0; j1 < n; j1++) {
                if(matrix[i1][j1] > res && matrix[i1][j1] <= k){
                    res = matrix[i1][j1];
                }
                dp[i1][j1] = matrix[i1][j1]; // 左上角和右下角都是同一个点的矩形，就是一个点。
                //(i1,j1)右边的那一行
                for (int j2 = j1 + 1; j2 < n; j2++) {
                    dp[i1][j2] = dp[i1][j2 - 1] + matrix[i1][j2];
                    //判断
                    if(dp[i1][j2] > res && dp[i1][j2] <= k){
                        res = dp[i1][j2];
                    }
                }
                //(i1,j1)下边的那一竖
                for (int i2 = i1 + 1; i2 < m; i2++) {
                    dp[i2][j1] = dp[i2-1][j1] + matrix[i2][j1];
                    //判断
                    if(dp[i2][j1] > res && dp[i2][j1] <= k){
                        res = dp[i2][j1];
                    }
                }
                //(i1,j1)右下方
                for (int i2 = i1 + 1; i2 < m; i2++) {
                    for (int j2 = j1 + 1; j2 < n; j2++) {
                        dp[i2][j2] = dp[i2-1][j2] + dp[i2][j2-1] - dp[i2-1][j2-1] + matrix[i2][j2];
                        //判断
                        if(dp[i2][j2] > res && dp[i2][j2] <= k){
                            res = dp[i2][j2];
                        }
                    }
                }
            }
        }
        return res;
    }
}

时间复杂度：O(m^2 n^2)

空间复杂度：O(mn)

运行结果：

请添加图片描述

解法3：数组滚动+暴力求最大子序和

参考了大佬的题解：https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k/solution/javacong-bao-li-kai-shi-you-hua-pei-tu-pei-zhu-shi/

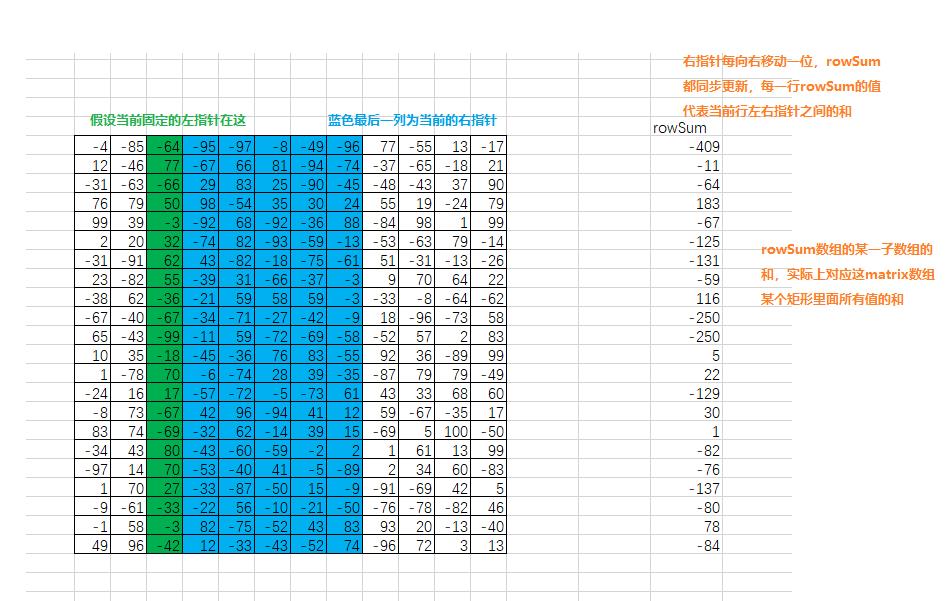
解题思路：

先用一指针固定某一列，再用另一指针向右扫描，扫描到的值都累加到rowSum数组中。

每向右扫描一趟，每扫完一趟，都对rowSum求最大子序和

这里求最大子序和采用的是暴力的方法，时间复杂度O(n^2) ，那么该程序整体还是4层循环，时间复杂度 O(m^2 n^2)

为了方便理解，先上个图吧：

请添加图片描述

class Solution {
    public int maxSumSubmatrix(int[][] matrix, int k) {
        int res = Integer.MIN_VALUE;
        int m = matrix.length;
        int n = matrix[0].length;
        int[] rowSum = new int[m]; //扫描的过程中每一行累积的值
        //第一层循环：固定的左边界
        for (int i = 0; i < n; i++) {
            //更换了左边界，相当于重新开始
            Arrays.fill(rowSum,0);
            //第二层循环：右边界
            for (int j = i; j < n; j++) {
                //右边界每向右移动一位，对应行的rowSum就要对应相加。
                for (int l = 0; l < m; l++) {
                    rowSum[l] += matrix[l][j];
                }
                //求最大子序和（第53题），这道题唯一不一样的地方在于这里限制了最大为k
                //法1：暴力求
                for (int i1 = 0; i1 < m; i1++) {
                    int tmp = 0;
                    for (int i2 = i1; i2 < m; i2++) {
                        tmp += rowSum[i2];
                        if(tmp > res && tmp <= k){
                            res = tmp;
                        }
                    }
                }
            }
        }
        return res;
    }
}

运行结果：

请添加图片描述

这题没法根据 53. 最大子序和题的方法进行优化，因为他限定了最大值为k，而该题目是没有限制的。

如果非是要求的话，可以先用53题的方法求出最大值，如果求出的最大值<=k，那么可以直接用，要不然还是暴力吧！

修改代码如下：

class Solution {
    public int maxSumSubmatrix(int[][] matrix, int k) {
        int res = Integer.MIN_VALUE;
        int m = matrix.length;
        int n = matrix[0].length;
        int[] rowSum = new int[m]; //扫描的过程中每一行累积的值
        //第一层循环：固定的左边界
        for (int i = 0; i < n; i++) {
            //更换了左边界，相当于重新开始
            Arrays.fill(rowSum, 0);
            //第二层循环：右边界
            for (int j = i; j < n; j++) {
                //右边界每向右移动一位，对应行的rowSum就要对应相加。
                for (int l = 0; l < m; l++) {
                    rowSum[l] += matrix[l][j];
                }
                //求最大子序和（第53题），这道题唯一不一样的地方在于这里限制了最大为k
                //法1：暴力求
//                for (int i1 = 0; i1 < m; i1++) {
//                    int tmp = 0;
//                    for (int i2 = i1; i2 < m; i2++) {
//                        tmp += rowSum[i2];
//                        if(tmp > res && tmp <= k){
//                            res = tmp;
//                        }
//                    }
//                }
                //法2：根据53题的方法求，要是求不出来再暴力
                int tmpRes = rowSum[0];
                int tmpSum = 0;
                for (int sum : rowSum) {
                    if (tmpSum >= 0) {
                        tmpSum += sum;
                    } else {
                        tmpSum = sum;
                    }
                    tmpRes = Math.max(tmpRes, tmpSum);
                }
                if (tmpRes <= k) {
                    //小于等于k，可以直接用
                    if (tmpRes > res) {
                        res = tmpRes;
                    }
                }else {
                    //要不然还是暴力求
                    for (int i1 = 0; i1 < m; i1++) {
                        int tmp = 0;
                        for (int i2 = i1; i2 < m; i2++) {
                            tmp += rowSum[i2];
                            if (tmp > res && tmp <= k) {
                                res = tmp;
                            }
                        }
                    }
                }
            }
        }
        return res;
    }
}

运行结果：

请添加图片描述

以上是关于363. 矩形区域不超过 K 的最大数值和（状态压缩dp）的主要内容，如果未能解决你的问题，请参考以下文章

Leetcode 363. 矩形区域不超过 K 的最大数值和

LeetCode 363 矩形区域不超过 K 的最大数值和

2022-01-20：矩形区域不超过 K 的最大数值和。给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。题目数据保证总会存在一

数据结构与算法之深入解析“矩形区域不超过K的最大数值和”的求解思路与算法示例

java 363.矩形的最大总和不大于K（＃1）.java