jzoj 1349 luogu P1390最大公约数 & 公约数的和

Posted 2021-08-18 SSL_ZZL

最大公约数 & 公约数的和

• 题面
• • Description
  • Input
  • Output
  • Sample Input
  • Sample Output
  • Data Constraint
• 解题思路
• Code

题面

Description

小菜的妹妹小诗就要读小学了！正所谓计算机要从娃娃抓起，小菜决定在幼儿园最后一段轻松的时间里教妹妹编程。
　　小菜刚教完gcd即最大公约数以后，一知半解的妹妹写了如下一段代码：
　　 sum:=0;
　　 for i:=1 to n-1 do
　　 for j:=i+1 to n do sum:=sum+gcd(i,j)

显然这个程序的效率是很低的，小明打算写一个更强的程序，在求出sum的同时比妹妹跑的更快。

Input

第一行一个整数t，即表示有t组数据
　　接下来t行，每行一个整数n

Output

t行，每行一个整数，表示n所对应的sum值

Sample Input

2
10
100

Sample Output

67
13015

Data Constraint

20%数据t≤100,n≤100
40%数据t≤1000,n≤2000
100%数据t≤10000,n≤1000000

---

解题思路

白捡道紫题，话说jzoj上的还是强化版的[瑟瑟发抖]

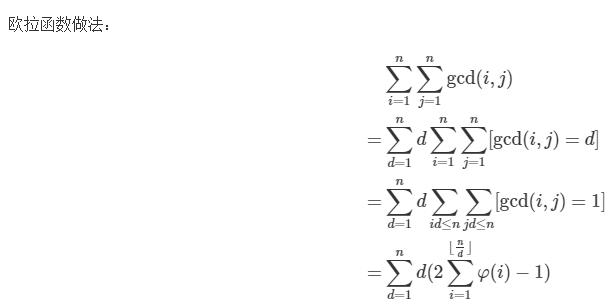
上图来自2018林卓铖
最后那条不是很看得懂，但上面的推演没有问题
数论补充站
其实就是求$gcd(i/d,j/d)=1$的情况有多少（d是n的因数），$j/d$的个数就是$\phi (i/d)$
那么答案就是$\sum \sum \phi （n/i）\ast i$

先用线性筛预处理出因数，在这个过程中还可以求φ（请看数论补充站）

---

Code

#include <algorithm>
#include <iostream>
#include <cstdio>
#define ll long long

using namespace std;

ll T, maxn;
ll n[100010], fn[1000100], f[1000100], ans[1000100], p[1010000];

void init() {
	fn[1] = 1;
	for(int i = 2; i <= maxn; i++) {
		if(!f[i])
			p[++p[0]] = i, fn[i] = i - 1;
		for(int j = 1; j <= p[0] && i * p[j] <= maxn; j++) {
			f[i * p[j]] = 1;
			if(i % p[j] == 0) {
				fn[i * p[j]] = fn[i] * p[j];
				break;
			} else
				fn[i * p[j]] = fn[i] * (p[j] - 1);
		}
	}
}

int main() {
	scanf("%lld", &T);
	for(int t = 1; t <= T; t++) {
		scanf("%lld", &n[t]);
		maxn = max(maxn, n[t]);
	}
	init();
	for(int i = 2; i <= maxn; i++)
		for(int j = 1; i * j <= maxn; j++)
			ans[i * j] += fn[i] * j;
	for(int i = 2; i <= maxn; i++)
		ans[i] += ans[i - 1];
	for(int i = 1; i <= T; i++)
		printf("%lld\\n", ans[n[i]]);
}