[NEFU ACM大一暑假集训 解题报告]尺取法
Posted 鱼竿钓鱼干
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[NEFU ACM大一暑假集训 解题报告]尺取法相关的知识,希望对你有一定的参考价值。
[NEFU ACM大一暑假集训 解题报告]尺取法
前四题为例题,学长讲过了,直接贴代码了。
题谱
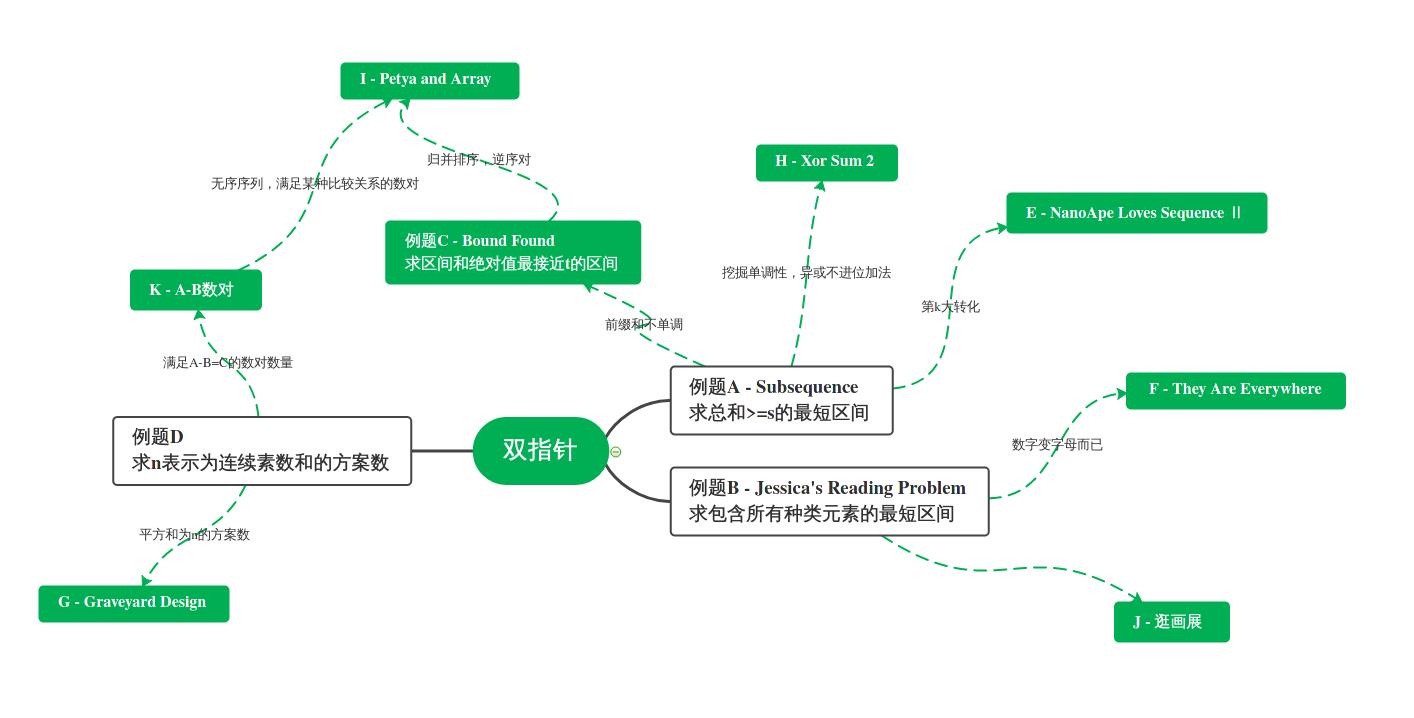
题目
A - Subsequence
求总和>=s的最短区间
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;
#define endl '\\n'
int T;
const int N=1e5+10;
int a[N],sum[N];
int n,s;
bool check(int i,int j){
return (sum[i]-sum[j-1])>=s;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&s);
int ans=1e9+7;
memset(sum,0,sizeof sum);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
sum[i]=sum[i-1]+a[i];
}
for(int i=1,j=1;i<=n;i++){//j左端点,i右端点
while(j<=i&&check(i,j))j++;//满足条件就要不断缩小区间
if(check(i,j-1))ans=min(ans,i-(j-1)+1);
}
if(ans==1e9+7)printf("0\\n");
else printf("%d\\n",ans);
}
return 0;
}
B - Jessica’s Reading Problem
求包含所有种类元素的最短区间
#include<cstdio>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
#define endl '\\n'
const int N=1000005;
int p,st,en,num,sum;
int a[N];
set<int>s;
map<int,int>mp;
int main(){
scanf("%d",&p);
for(int i=0;i<p;i++){
scanf("%d",a+i);
s.insert(a[i]);
}
num=s.size();
int ans=1e9+7;
while(1){
while(en<p&&sum<num){ //扩展区间延长右端点
if(mp[a[en]]==0)sum++;
mp[a[en]]++;
en++;
}
if(sum<num)break; //处理没有任何满足条件的区间
ans=min(ans,en-st); //更新答案
if(mp[a[st]]-1==0)sum--; //缩小区间缩短左端点
mp[a[st]]--;
st++;
}
printf("%d\\n",ans);
return 0;
}
C - Bound Found
这题主要和I题做区分,两者前缀和的都是非单调的,但是这题的话是前缀和的绝对值与其他的差值,所以可以排序后直接利用其前缀和的单调性。也就说说点对(i,j)和点对(j,i)的对于这题而言是完全相同的,只需保证输出答案的时候点对符合顺序即可
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long LL;
#define endl '\\n'
const int N=100005;
int n,m,t,ans,l,r;
struct Seg{
int sum;int id;
}seg[N];
int a[N];
bool cmp(Seg A,Seg B){return A.sum<B.sum;};
int main(){
while(~scanf("%d%d",&n,&m),n||m){
seg[0].id=0;seg[0].sum=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
seg[i].sum=seg[i-1].sum+a[i];
seg[i].id=i;
}
sort(seg,seg+1+n,cmp);
while(m--){
scanf("%d",&t);
int st=0,ed=1,tmp=1e9+7;
while(st<=n&&ed<=n){
int seg_sum=seg[ed].sum-seg[st].sum;
if(abs(seg_sum-t)<tmp){
tmp=abs(seg_sum-t);
ans=seg_sum;
l=seg[st].id,r=seg[ed].id;
}
if(seg_sum>t)st++;
else if(seg_sum<t)ed++;
else break;
if(st==ed)ed++;
}
if(r<l)swap(r,l);
printf("%d %d %d\\n",ans,l+1,r);
}
}
return 0;
}
其他写法
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<iostream>
using namespace std;
typedef long long LL;
#define endl '\\n'
const int N=100005;
int n,m,t,ans,l,r;
struct Seg{
int sum;int id;
}seg[N];
int a[N];
bool cmp(Seg A,Seg B){return A.sum<B.sum;};
int main(){
while(~scanf("%d%d",&n,&m),n||m){
seg[0].id=0;seg[0].sum=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
seg[i].sum=seg[i-1].sum+a[i];
seg[i].id=i;
}
sort(seg,seg+1+n,cmp);
while(m--){
scanf("%d",&t);
/*暴力
int tmp=1e9+7,l=0,r=0,ans=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=n;j++){
int seg_sum=abs(seg[j].sum-seg[i].sum);
if(abs(seg_sum-t)<tmp&&seg[j].id>seg[i].id){
tmp=abs(seg_sum-t);
ans=seg_sum;
l=seg[i].id+1,r=seg[j].id;
}
}
}*/
int tmp=1e9+7,left=0,right=1;//left不能和right相等
while(right<=n){
int seg_sum=seg[right].sum-seg[left].sum;
if(abs(seg_sum-t)<tmp){
tmp=abs(seg_sum-t);
l=seg[left].id,r=seg[right].id,ans=seg_sum;
}
if(seg_sum>t)left++;
else if(seg_sum<t)right++;
else break;
if(left==right)right++;
}
if(l>r)swap(l,r);
printf("%d %d %d\\n",ans,l+1,r);
}
}
return 0;
}
D - Sum of Consecutive Prime Numbers
求n表示为连续素数和的方案数
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
#define endl '\\n'
const int N=10010;
int primes[N],cnt;
bool st[N];
void get_primes(int n){
memset(st,0,sizeof st);
st[0]=st[1]=1;
for(int i=2;i<=n;i++){
if(!st[i])primes[++cnt]=i;
for(int j=1;primes[j]<=n/i;j++){
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
}
}
}
int n,ans,be,en,sum;
int main(){
get_primes(N);
while(~scanf("%d",&n),n){
be=en=1;ans=sum=0;
while(1){
if(sum==n)ans++;//更新答案
if(sum>=n){//收缩
sum-=primes[be];
be++;
}
else{
if(primes[en]<=n){//扩展
sum+=primes[en];
en++;
}
else break;//超出范围停止扩展结束
}
}
printf("%d\\n",ans);
}
return 0;
}
另外写法(和G题统一)
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
#define endl '\\n'
const int N=10010;
int primes[N],cnt;
bool st[N];
void get_primes(int n){
memset(st,0,sizeof st);
st[0]=st[1]=1;
for(int i=2;i<=n;i++){
if(!st[i])primes[++cnt]=i;
for(int j=1;primes[j]<=n/i;j++){
st[primes[j]*i]=true;
if(i%primes[j]==0)break;
}
}
}
int n,ans,be,en,sum;
int main(){
get_primes(N);
while(~scanf("%d",&n),n){
be=1,en=1;ans=sum=0;
for(;;){
while(primes[en]<=n&&sum<n){ //扩展右区间
sum+=primes[en];
en++;
}
if(sum<n)break; //处理没有任何满足的区间
if(sum==n)ans++; //更新答案
sum-=primes[be]; //缩小左区间
be++;
}
printf("%d\\n",ans);
}
return 0;
}
E - NanoApe Loves Sequence Ⅱ
题目问满足 区间内第k大的数>=m 的区间个数
第k大的数>=m,那么说明区间内至少有k个数>=m.
我们预处理把序列中>=m的标记为1,其余标记为0,然后求标记的前缀和数组。
接下来问题就变成了有多少个区间满足[l,r]的区间和>=k,看第一个例题A即可求解
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
#define endl '\\n'
int T;
const int N=200005;
LL a[N],s[N];
LL n,m,k;
bool check(int i,int j){
return s[i]-s[j-1]>=k;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%lld%lld%lld",&n,&m,&k);
memset(s,0,sizeof s);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]以上是关于[NEFU ACM大一暑假集训 解题报告]尺取法的主要内容,如果未能解决你的问题,请参考以下文章