《Involution：Inverting the Inherence of Convolution for Visual Recognition》论文笔记

Posted 2021-08-18 m_buddy

参考代码：involution

1. 概述

导读：CNN操作已经被广泛使CV领域，其具有空间无关性（spatial-agnostic）和通道特异性（channel-specific），前一个性质来源于在空间尺度上共享卷积参数，后一个性质来自于输出通道维度上的参数各不相同。在这篇文章中提出了一种性质与之相反的操作involution，通过学习的方式去得到卷积参数，之后经过维度变换之后与unfold之后的特征进行multiply-add，从而得到最后的输出结果，这里用到的multiply-add操作可以看作是self-attention的一种形式。因而整体上文章提出的involution操作具有了空间特异性和通道无关性，并且融合了self-attention的特性。以文章的操作作为基础模块去构建检测/分割任务网络，均在原来的基础上具有较大提升，而且由于这个操作本身的特性，使得其参数量/计算量有所减少。

现有的很多网络结构都是设计在算子CNN基础上的，其具有空间无关性与通道特异性，首先对这两个特性进行分析：

• 1）空间无关性：CNN算子中使用相同的参数在空间维度上进行滑动运算保证计算效率，同时也满足了平移不变性的需求。但是这样的方式却使得卷积核在不同空间位置上对于不同视觉任务的适应能力不足，而且其局部特性也限制了其感受野（增大感受野多是$3\ast 3$卷积的堆叠，而不是直接上采用大尺寸的卷积核）；
• 2）通道特异性：这里通过在输出通道上使用不同的卷积核从而使得网络中的信息被编码到了不同的channel中去。其实这样的形式是比较冗余的，文章后面的实验也表明通过分组的形式共享卷积参数，在一定的范围内对性能的影响很小，因而通道中存在较多的冗余；

对此文章提出了新的算子involution操作，通过算子设计将CNN的空间无关性和通道特异性进行对调，从而可以在相同条件下相比CNN算子减少计算量和参数量（后面内容会对其进行比较）。相比传统CNN算子新算子具有如下优点：

• 1）由于CNN算子参数量和计算量的原因，不能使用较大尺寸的卷积核，多是使用多个小卷积核堆叠的形式实现增大感受野。而由于文章的算子相对起来更加轻量化，这就使得可以使用更大尺寸的卷积核，从而增加会上下文信息的获取能力；
• 2）involution算子在优化的过程中不仅仅优化卷积核参数，还优化生成卷积核参数的参数（可能会对网络的训练带来一定难度，需实际验证），之后通过在空间维度上进行mutiply-add操作实现，卷积结果的加权组合，实现类似self-attention的范式，但相对self-attention操作省去了位置编码的部分；

2. 方法设计

2.1 回顾传统卷积操作

假定输入的特征图$X\in R^{H\ast W\ast C_i}$，输出的通道数量为$C_o$，则需要使用到的卷积核为$f\in R^{C_o\ast C_i\ast K\ast K}$，这里$K$是卷积核的大小。经过卷积之后输出的特征描述为：
$$Y_{i,j,k}=\sum _{c=1}^{C_i}\sum _{(u,v)\in {\Delta }_k}{f}_{k,c,u+\lfloor \frac{K}{2}\rfloor ,v+\lfloor \frac{K}{2}\rfloor }{X}_{i+u,j+v,c}$$
在一些情况下会使用卷积分组的形式共享卷积参数，从而减少计算量和参数量（其中深度卷积就是其中的极端例子）。则一个分组进行卷积其计算过程可以描述为：
$$Y_{i,j,k}=\sum _{(u,v)\in {\Delta }_K}{g}_{k,u+\lfloor \frac{K}{2}\rfloor ,v+\lfloor \frac{K}{2}\rfloor }{X}_{i+u,j+v,k}$$
其中$k$表示的是对应的分组切片。

2.2 involution操作

文章提出的新算子involution其操作流程可以参考下图：

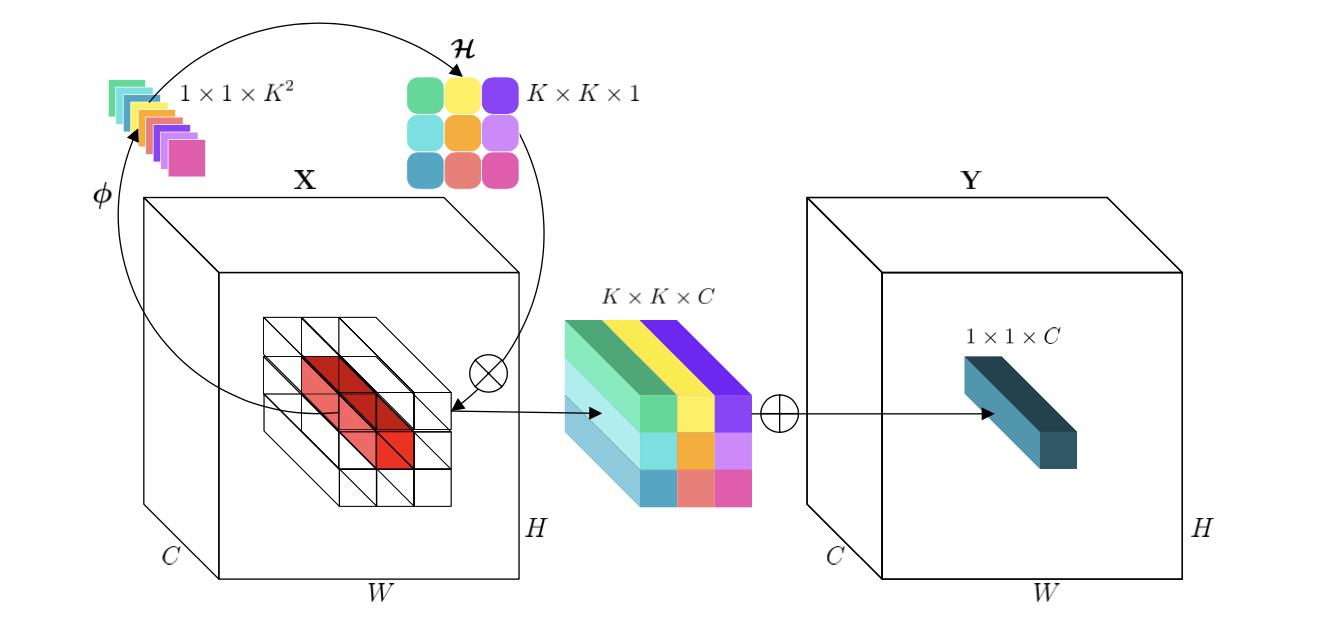
如上图所示，算法首先会在空间维度上对每个像素位置生成$K^2$个卷积参数，在具体实现中，是通过卷积的形式实现的，其数学表达描述为：
$${\mathcal{H}}_{i,j}=\varphi (X_{i,j})=W_1\sigma (W_o{X}_{i,j})$$
这里$X_{i,j}$代表的是空间维度上某个点的向量，$W_0\in R^{\frac{C}{r}\ast C\ast 1\ast 1},W_1\in R^{(K\ast K\ast G)\ast \frac{C}{r}\ast 1\ast 1}$，$r$是通道缩减比例。之后会对生成的卷积参数展平与分组，再与输入的特征（经过unfolf操作）进行Multiply-Add操作，其中一个分组的运算描述为：
$$Y_{i,j,k}=\sum _{(u,v)\in {\Delta }_K}{\mathcal{H}}_{i,j,u+\lfloor \frac{K}{2}\rfloor ,v+\lfloor \frac{K}{2}\rfloor ,\lceil \frac{kG}{C}\rceil }{X}_{i+u,j+v,k}$$
下面的伪代码很好展示了其计算的流程：

# B: batch size, H: height, W: width
# C: channel number, G: group number
# K: kernel size, s: stride, r: reduction ratio
################### initialization ###################
o = nn.AvgPool2d(s, s) if s > 1 else nn.Identity() reduce = nn.Conv2d(C, C//r, 1)
span = nn.Conv2d(C//r, K*K*G, 1)
unfold = nn.Unfold(K, dilation, padding, s) 
#################### forward pass #################### 
x_unfolded = unfold(x) # B,CxKxK,HxW
x_unfolded = x_unfolded.view(B, G, C//G, K*K, H, W)
# kernel generation, Eqn.(6)
kernel = span(reduce(o(x))) # B,KxKxG,H,W
kernel = kernel.view(B, G, K*K, H, W).unsqueeze(2)  # B, G, 1, K*K, H, W
# Multiply-Add operation, Eqn.(4)
out = mul(kernel, x_unfolded).sum(dim=3) # B,G,C/G,H,W out = out.view(B, C, H, W)
return out

involution和CNN参数量和计算量比较：
在输入和输出通道都为$C$，卷积核都为$Involution：空间不共享？可完全替代卷积的高性能算子\; CVPR\; 2021$

Java Inverting Switch语句

Applying and Inverting Transformations [on mask]

改进YOLO系列 | CVPR 2021 | Involution：超越convolution和self-attention的神经网络算子

阅读笔记Inverting Gradients -- How easy is it to break privacy in federated learning?

五期邹昱夫CCF-A（NeurIPS'19）Inverting gradients-how easy is it to break privacy in federated learning?