Leetcode——滑动窗口的最大值

Posted 2021-08-17 Yawn,

1. 题目

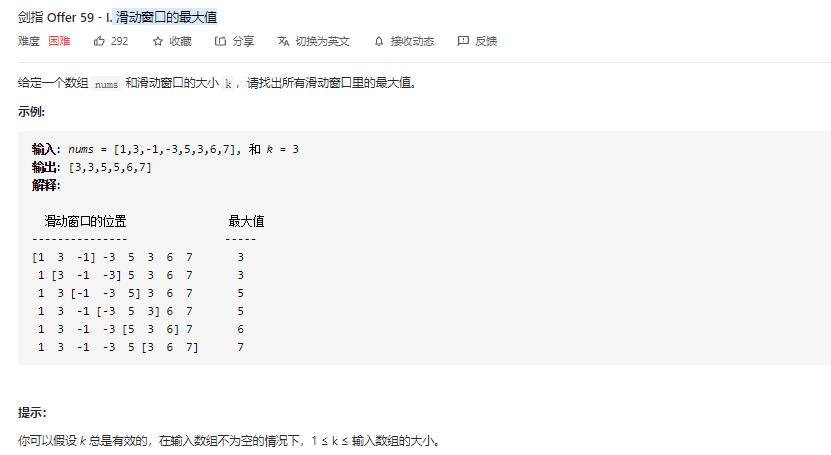
2. 题解

（1）优先队列

• 将数组 nums 的前 k 个元素放入优先队列中
• 每当我们向右移动窗口时，我们就可以把一个新的元素放入优先队列中，此时堆顶的元素就是堆中所有元素的最大值
• 然而这个最大值可能并不在滑动窗口中，在这种情况下，这个值在数组 \\textit{nums}nums 中的位置出现在滑动窗口左边界的左侧
• 当我们后续继续向右移动窗口时，这个值就永远不可能出现在滑动窗口中了，我们可以将其永久地从优先队列中移除。
• 断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。
• 为了方便判断堆顶元素与滑动窗口的位置关系，可以在优先队列中存储二元组(num,index)，表示元素 num 在数组中的下标为index。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        // 1. 优先队列存放的是二元组(num,index) : 
       		//大顶堆（元素大小不同按元素大小排列，元素大小相同按下标进行排列）
            // num :   是为了比较元素大小
            // index : 是为了判断窗口的大小是否超出范围
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>(){
            public int compare(int[] pair1,int[] pair2){
                return pair1[0] != pair2[0] ? pair2[0] - pair1[0]:pair2[1] - pair1[1];
            }
        });

        // 2. 优选队列初始化 : k个元素的堆
        for(int i = 0;i < k;i++){
            pq.offer(new int[]{nums[i],i});
        }

        // 3. 处理堆逻辑
        int[] res = new int[n - k + 1];         // 初始化结果数组长度 ：一共有 n - k + 1个窗口
        res[0] = pq.peek()[0];                  // 初始化res[0] ： 拿出目前堆顶的元素
        for(int i = k;i < n;i++){               // 向右移动滑动窗口
            pq.offer(new int[]{nums[i],i});     // 加入大顶堆中
            while(pq.peek()[1] <= i - k){       // 将下标不在滑动窗口中的元素都干掉
                pq.poll();                      // 维护：堆的大小就是滑动窗口的大小
            }   
            res[i - k + 1] = pq.peek()[0];      // 此时堆顶元素就是滑动窗口的最大值
        }
        return res;
    }
}

（2）单调队列

• 遍历数组，将 数 存放在双向队列中，并用 L,R 来标记窗口的左边界和右边界。
• 队列中保存的并不是真的 数，而是该数值对应的数组下标位置，并且数组中的数要从大到小排序。
• 如果当前遍历的数比队尾的值大，则需要弹出队尾值，直到队列重新满足从大到小的要求。
• 刚开始遍历时，L 和 R 都为 0，有一个形成窗口的过程，此过程没有最大值，L 不动，R 向右移。
• 当窗口大小形成时，L 和 R 一起向右移，每次移动时，判断队首的值的数组下标是否在 [L,R] 中，如果不在则需要弹出队首的值，当前窗口的最大值即为队首的数。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) 
    {
        int len = nums.length;
        if(nums == null || len < 2)
            return nums;

        // 双向队列 保存当前窗口最大值的数组位置 保证队列中数组位置的数值按从大到小排序
        // 结果数组
        int[] result = new int[len - k + 1];
        Deque<Integer> queue = new LinkedList<>();

        for(int i = 0; i < len; i++){
            while(!queue.isEmpty() && nums[queue.peekLast()] <= nums[i])
                queue.pollLast();

            // 添加当前值对应的数组下标
            queue.addLast(i);

            // 判断当前队列中队首的值是否有效
            if(queue.peek() <= i - k)
                queue.poll();
            
            //当窗口长度为k时 保存当前窗口中最大值
            //当前窗口范围：[i-k+1,i]
            if(i - k + 1 >= 0){
                result[i - k + 1] = nums[queue.peek()];
            }
        }
        return result;
    }
}