2021牛客多校2 C Draw Grids

Posted 2021-08-17 你可以当我没名字

链接：https://ac.nowcoder.com/acm/contest/11253/C
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

ZYT and LBC decided to play a game.

They will alternately do the following operation.

• ​ Pick 4 integers a,b,c,d(1≤a,c≤na,b,c,d(1\\leq a,c \\leq na,b,c,d(1≤a,c≤n and 1≤b,d≤m)\\ 1\\leq b,d \\leq m) 1≤b,d≤m) , where ∣a−c∣+∣b−d∣=1{ |a-c|+|b-d|=1}∣a−c∣+∣b−d∣=1 , and draw a straight segment between point (a,b){(a,b)}(a,b) and point (c,d){(c,d)}(c,d). The segment shouldn’t overlap with a segment that already exists.

• ​ In any time, the segments shouldn’t form a polygon. That is, there exists no sequence of distinct points (x0,y0),(x1,y1),⋯,(xk−1,yk−1){(x_0,y_0),(x_1,y_1),⋯,(x_{k−1},y_{k−1})}(x0,y0),(x1,y1),⋯,(xk−1,yk−1) satisfying for each integer 0≤u<k0 \\leq u < k0≤u<k，there is a segment between (xu,yu)(x_u,y_u)(xu,yu) and (x(u+1) mod k,y(u+1) mod k)(x_{ (u+1)\\ \\text{mod}\\ k },y_{ (u+1)\\ \\text{mod}\\ k })(x(u+1) mod k,y(u+1) mod k).

  The player who can’t perform an operation during his move loses.

  Determine whether ZYT can win considering that both players play optimally and ZYT starts.

  

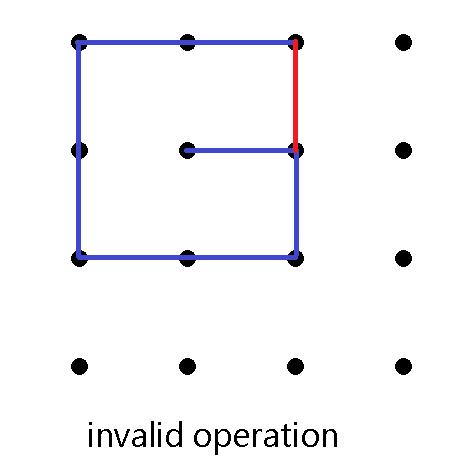
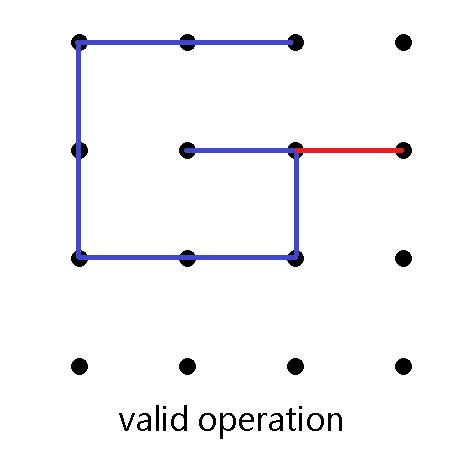
输入描述:

The input consists of one line containing two integers n{n}n and m{m}m.

输出描述:

Print "YES"(without quote) if ZYT can win and "NO"(without quote) if ZYT can't.

示例1

输入

[复制](javascript:void(0)😉

1 3

输出

[复制](javascript:void(0)😉

NO

示例2

输入

[复制](javascript:void(0)😉

2 2

输出

[复制](javascript:void(0)😉

YES

备注:

It is guaranteed that 1≤n,m≤41\\le n,m\\le 41≤n,m≤4.

思路与代码

读懂题就会了,没啥好讲的

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <iostream>
#include <sstream>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <vector>
#include <limits.h>
#include <assert.h>
#include <functional>
#include <numeric>
#include <ctime>
//#include <ext/pb_ds/assoc_container.hpp>
//#include <ext/pb_ds/tree_policy.hpp>
#define pb          push_back
#define ppb         pop_back
#define lbnd        lower_bound
#define ubnd        upper_bound
#define endl        '\\n'
#define mll         map<ll,ll>
#define msl         map<string,ll>
#define mls         map<ll, string>
#define rep(i,a,b)    for(ll i=a;i<b;i++)
#define repr(i,a,b) for(ll i=b-1;i>=a;i--)
#define trav(a, x)  for(auto& a : x)
#define pll         pair<ll,ll>
#define vl          vector<ll>
#define vll         vector<pair<ll, ll>>
#define vs          vector<string>
#define all(a)      (a).begin(),(a).end()
#define F           first
#define S           second
#define sz(x)       (ll)x.size()
#define hell        1000000007
#define DEBUG       cerr<<"/n>>>I'm Here<<</n"<<endl;
#define display(x)  trav(a,x) cout<<a<<" ";cout<<endl;
#define what_is(x)  cerr << #x << " is " << x << endl;
#define ini(a)      memset(a,0,sizeof(a))
#define ini2(a,b)   memset(a,b,sizeof(a))
#define rep(i,a,b)  for(int i=a;i<=b;i++)
#define sc          ll T;cin>>T;for(ll Q=1;Q<=T;Q++)
#define lowbit(x)   x&(-x)
#define ordered_set tree<ll, null_type,less<ll>, rb_tree_tag,tree_order_statistics_node_update>
#define FAST ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define DBG(x) \\
    (void)(cout << "L" << __LINE__ \\
    << ": " << #x << " = " << (x) << '\\n')
#define TIE \\
    cin.tie(0);cout.tie(0);\\
    ios::sync_with_stdio(false);

//using namespace __gnu_pbds;

using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const double PI = acos(-1.0);
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;
const int maxn = 2000;
const int N = 500009;

bool cmp(int a,int b){
	return a>b;
}

void solve(){
	int n,m,ans;
	while(cin>>n>>m){
		ans = n*m;
		if(ans%2==0){
			cout<<"YES"<<endl;
		}else{
			cout<<"NO"<<endl;
		}
	}
}

int main()
{
//    #ifndef ONLINE_JUDGE
//    freopen ("input.txt","r",stdin);
//    #else
//    #endif
	solve();
//    sc{solve();}
//    sc{cout<<"Case "<<Q<<":"<<endl;solve();}
}