jzoj3539清华集训2014模拟数论高斯消元折射伤害

Posted 2021-08-15 SSL_ZZL

【清华集训2014模拟】折射伤害

• 题面
• • Description
  • Input
  • Output
  • Sample Input
  • Sample Output
  • Data Constraint
• 解题思路
• Code

题面

Description

在一个游戏中有n个英雄，初始时每个英雄受到数值为ai的伤害，每个英雄都有一个技能“折射”，即减少自己受到的伤害，并将这部分伤害分摊给其他人。对于每个折射关系，我们用数对(xi,yi,zi)来表示xi将自己受到伤害去掉zi的比例，将这些伤害转移给yi（xi,yi是整数，zi是实数）。
求出经过反复折射后最后每个英雄受到的实际总伤害。

Input

第一行一个正整数：n，表示有n个英雄，第二行n个整数Ai，依次表示每个英雄受到的初始伤害。第三行一个正整数m，表示有m对折射关系。接下来m行，每行三个数xi,yi,zi，表示xi将自己受到伤害去掉zi的比例，将这些伤害转移给yi。

Output

输出n行，第i行表示第i个英雄最后受到的实际总伤害。保留六位小数。

Sample Input

3
1 0 2
3
1 2 0.3000
1 2 0.2000
2 1 0.5000

Sample Output

0.666667
0.333333
2.000000

Data Constraint

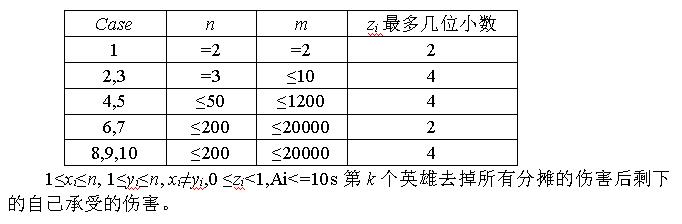
Source / Author: damage by 高欣

---

解题思路

学了一小时的高斯消元yyy

当前人受到的总伤害 = 初始伤害 + 别人受到的总伤害 * 转移给当前人的比例(输入的时候累计一下就好了)
$$a_i+\sum _{j=1;j\ne i}^n{f}_j\ast z_{j,i}=f_i$$
移项
$$\sum _{j=1;j\ne i}^n{f}_j\ast z_{j,i}-f_i=-a_i$$
一个多元一次方程组，用高斯消元求解

最终答案 = 受到的总伤害 * （1-转移给别人的伤害(这个也要累计））

---

Code

#include <iostream>
#include <cstdio>
#include <cmath>
#define db double

using namespace std;

int n, m, x, y;
db c, f[210][210], p[210];

int main() {
	scanf("%d", &n);
	for(int i = 1; i <= n; i++) {
		scanf("%lf", &f[i][n + 1]);
		f[i][n + 1] = -f[i][n + 1];
		f[i][i] = -1;  //-f[i]：f[i]的系数是-1
	}
	scanf("%d", &m);
	for(int i = 1; i <= m; i++) {
		scanf("%d %d %lf", &x, &y, &c);
		f[y][x] += c, p[x] += c;
	}
	for(int i = 1; i <= n; i++) {  //高斯消元模板
		int maxn = i;
		for(int j = i + 1; j <= n; j++)
			if(abs(f[j][i]) > abs(f[maxn][i]))
				maxn = j;
		for(int j = i; j <= n + 1; j++)
			swap(f[i][j], f[maxn][j]);
		for(int j = 1; j <= n; j++) {
			if(j == i) continue;
			db tmp = f[j][i] / f[i][i];
			for(int t = i + 1; t <= n + 1; t++)
				f[j][t] -= f[i][t] * tmp;
		}
	}
	for(int i = 1; i <= n; i++)
		printf("%.6lf\\n", f[i][n + 1] / f[i][i] * (1.0 - p[i]));
}