jzoj19302010集训队出题期望彩色圆环

Posted 2021-08-15 SSL_ZZL

【2010集训队出题】彩色圆环

• 题面
• • Description
  • Input
  • Output
  • Sample Input
  • • 【输入样例一】
    • 【输入样例二】
  • Sample Output
  • • 【输出样例一】
    • 【输出样例二】
    • Hint
    • 【数据规模和约定】
    • 【评分标准】
• 解题思路
• Code

题面

Description

小A喜欢收集宝物。一天他得到了一个圆环，圆环上有N颗彩色宝石，闪闪发光。小A很爱惜这个圆环，天天把它带在身边。
　　一天，小A突然发现圆环上宝石的颜色是会变化的。他十分惊讶，仔细观察这个圆环后发现，圆环上宝石的颜色每天变化一次，而且每颗宝石的颜色都等概率地为特定的M种颜色之一。小A发现了这个秘密后，对圆环更是爱不释手，时时刻刻都在研究。
　　又经过了一段时间，小A发现因为圆环上宝石的颜色不断变化，圆环有时会显得比其他时候更美丽。为了方便比较，小A这样定义圆环的“美观程度”：
　　设圆环上相同颜色的宝石构成的连续段长度分别为a1, a2, …, an；
　　定义圆环的“美观程度” R= a1 * a2 * … * an。
　　以图一给出的圆环为例，有a1 = 3, a2 = 2, a3 = 1，故R = 6。
　　

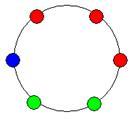
现在小A想知道，在上述前提下，圆环的“美观程度”的期望值E®是多少。因为如果知道了E®，他就可以判断每天变化出的新圆环是否比一般情况更美丽。
　　说明：“美观程度”的期望值即为对每种可能的圆环状态的“美观程度”与其出现概率的乘积进行求和所得的值。

Input

输入文件circle.in仅有一行，该行给出依次两个正整数N, M，分别表示宝石的个数和宝石在变化时可能变成的颜色种类数。

Output

输出文件circle.out应仅有一行，该行给出一个实数E®，表示圆环的“美观程度”的期望值。

Sample Input

【输入样例一】

3 2

【输入样例二】

200 1

Sample Output

【输出样例一】

2.25

【输出样例二】

200

Hint

【数据规模和约定】

20%的数据满足1 ≤ N, M ≤ 8；
50%的数据满足1 ≤ N, M ≤ 25；
100%的数据满足1 ≤ N ≤ 200, 1 ≤ M ≤ 10^9。

【评分标准】

对每个测试点，若你给出的E®与标准程序给出的E®’的相对误差不超过10-7，则该测试点得满分；否则该测试点得零分。
说明：相对误差　$\gamma =|E(R)-E(R{)}^{\prime }|/(E(R{)}^{\prime })$ .
Source / Author: 2010集训队出题 彩色圆环 circle by 吴佳俊

---

解题思路

我数论真的好烂aaa

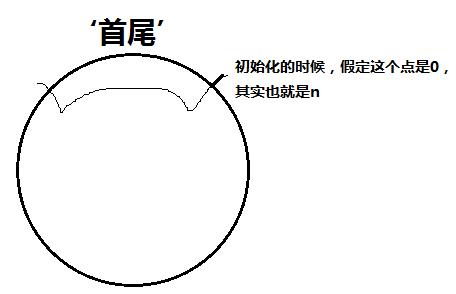
设f[i][0/1]为以任意起点（0）到i的项链，头尾不相同/相同的期望
一段珠宝同色的概率* 颜色的可能 * 同色的价值（即同色珠宝长度） = 这一段的期望

#转移的三种情况

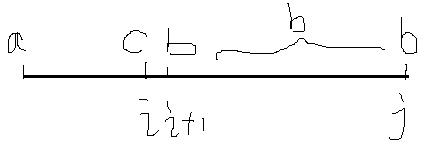
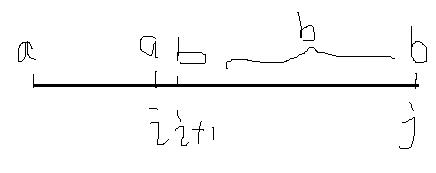
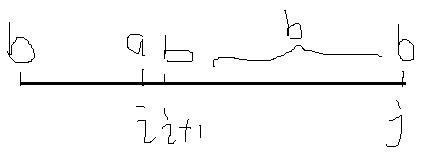
#初始值

#统计答案

---

Code

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

int n, m;
double ans, p[300], f[300][300];

int main() {
	scanf("%d %d", &n, &m);
	p[0] = 1.0, m = 1.0 * m;
	for(int i = 1; i <= n; i++)  //先把i个珠宝同色的概率求出来
		p[i] = p[i - 1] / m;
	f[0][1] = 1.0;
	for(int i = 0; i <= n; i++) {
		for(int j = i + 1; j <= n; j++) {
			f[j][0] += f[i][0] * p[j - i] * (m - 2.0) * (double)(j - i); 
			  //第一种情况，头、i各有一个颜色，所以j的颜色选择只有m-2
			f[j][0] += f[i][1] * p[j - i] * (m - 1.0) * (double)(j - i); 
			  //第二种，i与头颜色相同，占一种颜色，所以j的颜色选择有m-1
			f[j][1] += f[i][0] * p[j - i] * (double)(j - i);
			  //第三种，j与头颜色相同，头的颜色已经选了，所以j位置只用算概率*长度，颜色不用选
		}
	}
	//将首和尾并在一起，合称一下‘首尾’
	ans = p[n] * n * m;  //一整条项链都是一种颜色的期望
	for(int i = 1; i < n; i++)  //枚举‘首尾’长度
		ans += f[n - i][0] * i * i * p[i] * m;
		  //不同的分割方案 * 长度i * ‘首尾’颜色相同的概率 * m种颜色（因为是首的颜色所以什么颜色都可以选）
		  //不同的分割方案:在‘首尾’中找一个点，切开，分成首和尾，可以选定的点有i种
	printf("%.10lf", ans);
}