子数组/子序列/子串 dp问题的总结

Posted 2021-08-15 C_YCBX Py_YYDS

文章目录

• 关于这一类问题的相同处理
• 两个例题探讨子数组dp的处理方式
• • 例题一：连续子数组的最大和
  • 例题二：最长连续递增子序列

关于这一类问题的相同处理

• 关于序列 / 子数组 / 子串问题的 dp 我们一般都用 dp[i] 代表以 nums[i] 结尾的子序列 / 子数组 / 子串的相应最优值.
• 子序列和子数组dp处理的最大差别：

1. 子序列 dp 你无法确定是否就是 dp[i-1] (或者说 nums[i-1] )和现在的 dp[i] 形成关系。
2. 而子数组的 dp 一定是和前面的 [i-1] 形成关系。

两个例题探讨子数组dp的处理方式

例题一：连续子数组的最大和

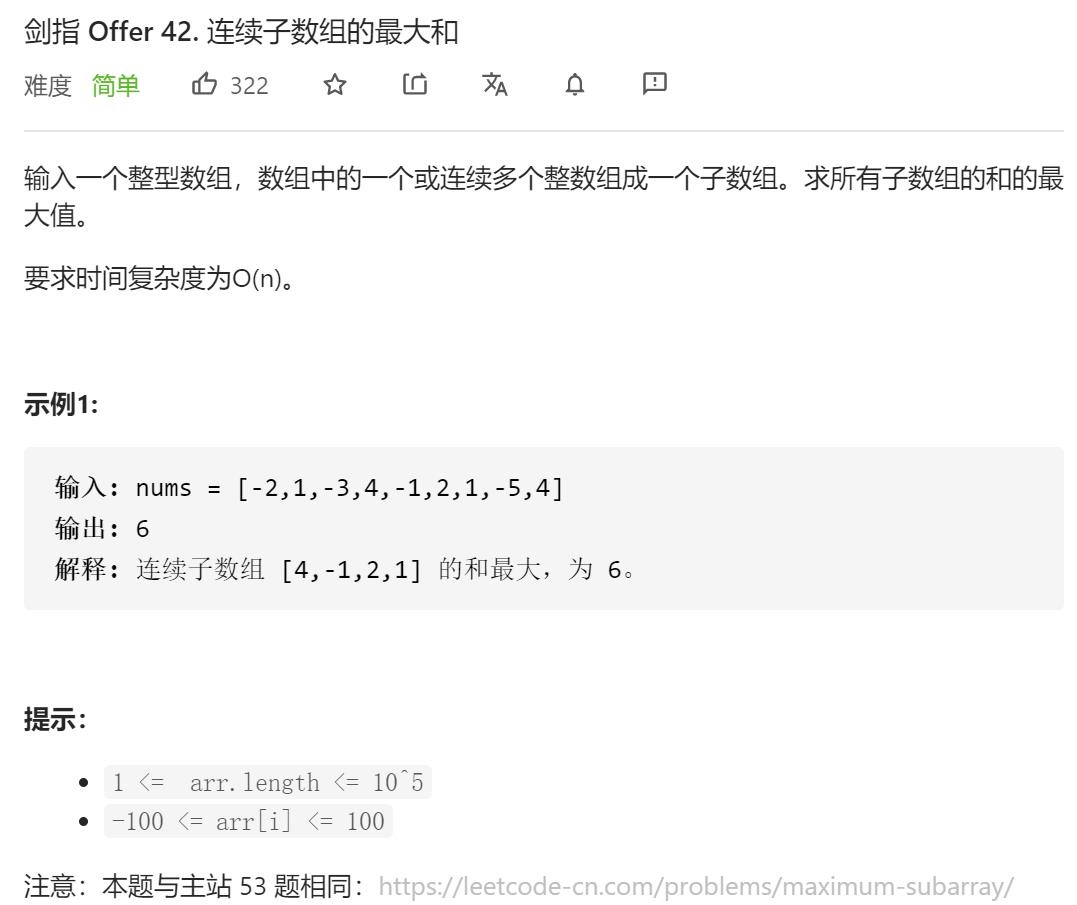
用dp[i]代表以nums[i]结尾的子数组的最大和。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        int dp[n];memset(dp,0,sizeof(dp));
        dp[0] = nums[0];
        for(int i=1;i<n;i++){
            if(dp[i-1]>0)
                dp[i] += dp[i-1];
            dp[i] += nums[i];
        }
        return *max_element(dp,dp+n);
    }
};

优化为O(1)空间

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        int pre = nums[0];
        int cur;
        int res = pre;
        for(int i=1;i<n;i++){
            if(pre>0)
                cur = pre+nums[i];
            else
                cur = nums[i];
            pre = cur;
            res = max(res,cur);
        }
        return res;
    }
};

例题二：最长连续递增子序列

LCS非常常见且经典，题目就不列了，直接分析。

该题中dp[i[明显的含义就是以 nums[i] 结尾的序列，最长的递增长度。可以对比 nums[i-1]<nums[i] 来决定是否继承 dp[i-1]

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int n = nums.size();
        if(n==0)
            return 0;
        int dp[n];
        fill(dp,dp+n,1);
    for(int i=1;i<n;i++){
        if(nums[i-1]<nums[i])
            dp[i] = dp[i-1]+1;
    }
        return *max_element(dp,dp+n);
    }
};

空间优化

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int n = nums.size();
        if(n==0)
            return 0;
        int pre = 1;
        int cur;
        int res = pre;
    for(int i=1;i<n;i++){
        if(nums[i-1]<nums[i])
            cur = pre+1;
        else  
            cur = 1;
        pre = cur;
        res = max(res,cur);
    }
        return res;
    }
};