(转)红包随机算法&微信群红包随机算法

Posted 2021-08-15 jfcat

通过这篇文章算是把微信群红包的算法弄明白了

1.前言

因疫情影响，部门 2021 年会以线上直播的形式进行，通过微信小程序展开。为活跃年会氛围，年会直播间会有抢红包环节。因产品要求，红包金额要随机生成，所以这里涉及到指定红包总额、数量和最大最小值情况下如何生成红包金额。

可以看出，红包随机金额生成的输入是一个四元组 <sum, num, min, max>，其中 sum 是红包总额，num 是红包数量，min 和 max 分别是红包最小最大值。所以这里可以抽象成如下算法：

input: <sum, num, min, max>
output: 随机红包金额数组

因为法币都有最小单位，比如人民币是分，所以上面输入四元组均可视为整数。

2.参考微信群红包算法

本质上，这和微信群红包没什么区别，发出一个固定总金额的红包，指定红包数量，那么随机分配红包金额时需要满足哪些规则？ （1）所有人抢到金额之和等于红包总金额，不能超过，也不能少于； （2）抢到的红包金额至少是一分钱； （3）要保证抢到红包的人获取到的红包金额是随机的。

实际上，微信群红包的 min 是 1 分钱，max 是剩余红包金额均值的两倍，为什么是这两个值，因为这么做会保证随机值的期望值等于均值，来保证不会因为抢红包的先后顺序而造成不公平。这两个值是算法内设的，不提供给用户指定。另外总金额 sum 和数量 num 是由用户指定的。

为什么微信群红包要搞一个最大上限，因为如果不设置一个最大上限，会出现一种不公平的现象。就是越在前边领取红包的同学，其可随机范围越大，获得大额红包的几率也越高。一旦前边的同学随机到一个较大的金额，后边的同学可以随机的范围就逐步收窄，抢红包就变成了一个拼手速的游戏了。

实际上，微信群红包采用的是二倍均值法，也就是每次随机上限为剩余红包金额均值的两倍。微信群红包金额分配算法是这样的：

每次抢红包直接随机，随机的范围是[1, 剩余红包金额均值的两倍]，单位分

这个公式，保证了每次随机金额的平均值是相等的，不会因为抢红包的先后顺序而造成不公平。

实际上微信群红包的算法虽然公平，但是有个缺陷，不过这个微信产品同学可以接受，只是对于用户来说体验并不是那么友好，因为有时发个群红包会出现下面这种最后一个红包金额非常大的情况。

 

 

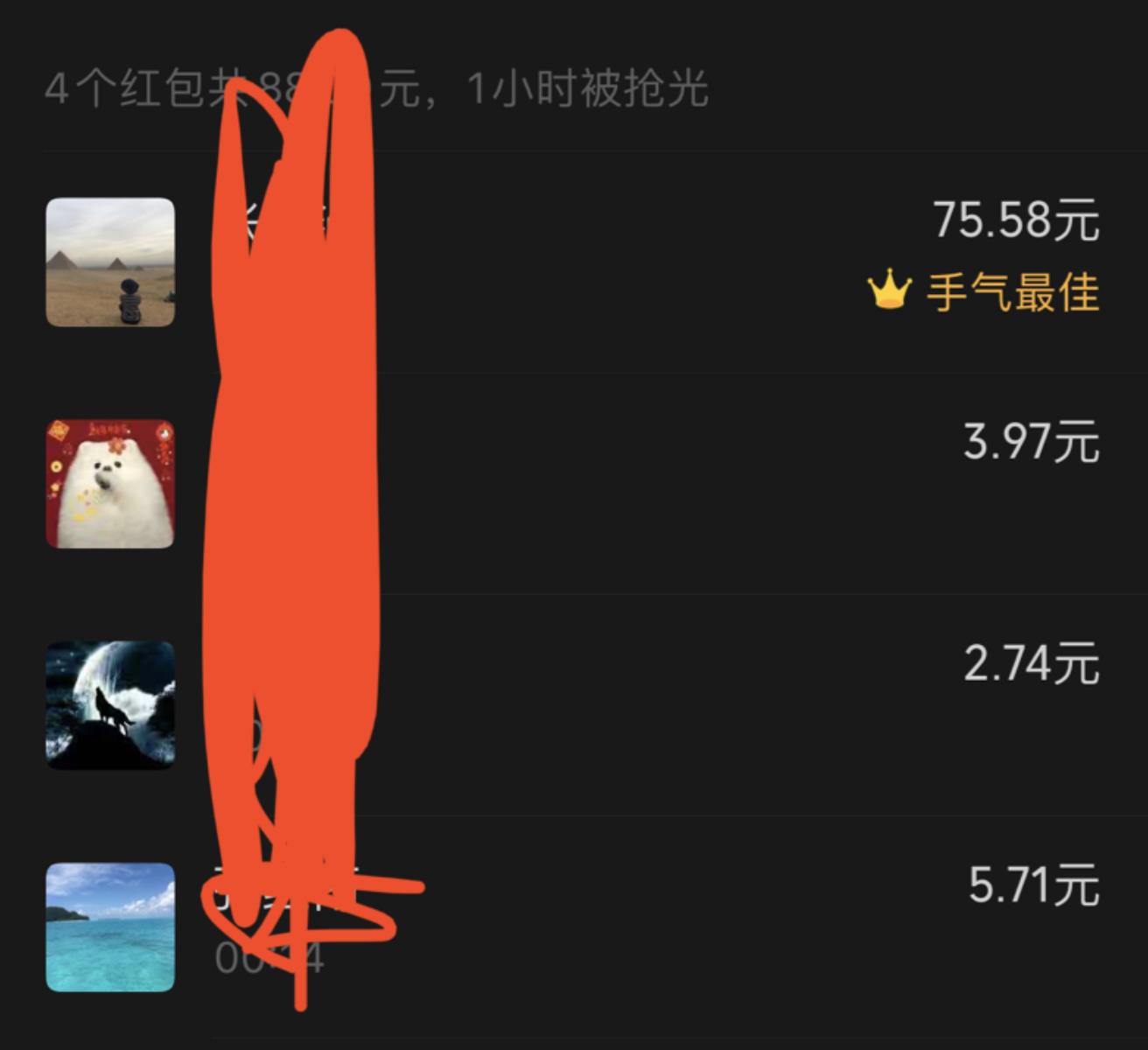
出现这种情况的原因是，上面的随机上限 max 为剩余红包金额均值的两倍，对于最后一个红包是无法生效的。当然，出现这种情况的概率非常小。

这说明了一个什么问题呢？红包金额随机分配算法不是一个标准算法，而是产品逻辑。 如果你是产品同学，你完全可以搞一个你想要的随机分配算法，比如随机范围严格在 [min, max] 之间，或者像微信群红包那样，每次抢红包时，max 是动态变化的。

这里说下大家最关心的问题，就是如何才能抢到大红包。通过上面的介绍，结论就是除了最后一个红包金额是有可能大于均值的两倍，其他都是在 [0.01 - 剩余均值*2] 之间随机。如果红包数量充足，那么最后一位抢才有可能获得大红包。但绝大部分情况是僧多粥少，需要拼手速才能抢到红包，这种情况下，你不能保证你是最后那位抢到红包的人。

3.一个可用的随机算法

此次年会产品同学开始跟我说需要像微信群红包那样的随机分配红包金额，但是仔细研究了微信群红包的算法，才发现产品同学想要的效果和微信群红包并不同，她想要的是红包金额严格随机范围在 [min, max]。

在实现时要满足如下几个条件： （1）所有人抢到金额之和等于红包总金额，不能超过，也不能少于； （2）抢到的红包金额在 [min, max] 之间； （3）要保证抢到红包的人获取到的红包金额是随机的。

下面给一个可行的随机分配算法。

// min 最小金额分 max 最大金额分 num 红包数量 sum 红包总额分
input：<min, max, num, sum>

// 参数合法性校验
step 1: min*num <= sum <= max*num 
step 2: 将 num 个在 min 填入数组
step 3: 循环随机一个范围为 [0, max - min] 数加到最小值数组中。如果随机数大于剩余金额，则取剩余金额作为随机数；如果累加值大于最大值，则取最大值与原值差值作为随机数。如果剩余金额为 0 结束循环
step 4: 如果均值靠近 min 或 max，第三步分别会出现很多 min 或者 max，看起来不够随机。这里需要经过一轮或多轮遍历，将 (min, max) 之间的数减掉部分给到 min 或者从 max 获得部分
step 5: 打乱数组顺序

注意，在第四步消除最小值或最大值，是控制在一定比例还是完全消除，也是一个产品逻辑，需要由产品同学来定。下面的实现示例，只进行一轮循环，可能会存在少量最小值或最大值。

下面以 JS 为例，给出实现。

// brief: 获取随机整数 [min, max]
function random(min, max) {
  const range = max - min;
  const rand = Math.round(Math.random() * range);
  return min + rand;
}

// brief: 消除最小值和最大值
function smooth(min, max, arr) {
  for (let i = 0; i < arr.length; i++) {
    if (!(min < arr[i] && arr[i] < max)) {
      continue
    }
    for (let j = 0; j < arr.length; j++) {
        // 消除最小值
        if (arr[j] === min) {
          let rm = Math.floor((arr[i] - min)/10)
          arr[i] -= rm
          arr[j] += rm
          break
        }
        // 消除最大值
        if (arr[j] === max) {
          let rm = Math.floor((max - arr[i])/10)
          arr[i] += rm
          arr[j] -= rm
          break
        }
    }
  }
}

// brief: 打乱数组顺序
function shuffle(arr) {
  arr.sort(() => Math.random() - 0.5);
}

// brief: 生成随机整数数组
function randnum(min, max, num, sum) {
  // step 1 检查参数
  if (min <= 0 || max <= 0 || num <= 0 || sum <= 0) {
    return [];
  }
  if (!(min * num <= sum && sum <= max * num)) {
    return [];
  }

  // step 2 将 num 个在 min 填入数组
  var arr = new Array(num).fill(min);
  
  // step 3 循环随机生成[0, max-min]加到最小值数组
  let leftTotal = parseInt(sum - min*num);
  LABEL:
  while(true) {
    for (let i = 0; i < num; i++) {
        let rand = random(0, parseInt(max-min));
        // 如果随机数大于剩余金额，则取剩余金额作为随机数
        if (rand > leftTotal) {
            rand = leftTotal;
        }
        // 如果累加值大于最大值，则取最大值与原值差值作为随机数
        if (arr[i] + rand > max) {
            rand = max - arr[i];
        }
        arr[i] += rand;
        leftTotal -= rand;
        if (leftTotal === 0) {
            break LABEL;
        }
    }
  }
  
  // step 4 消除大部分最小值和最大值
  smooth(min, max, arr)
  
  // step 5 打乱数组顺序
  shuffle(arr)
  
  return arr;
}

上面的代码可以在 Online NodeJS IDE 执行。

下面采用两组入参，均值分别靠近最小值和最大值来观察多次运行后的输出结果。

第一组入参，最小金额 5 元，最大金额 50 元，数量 10 个，总金额 100 元。均值 10 靠近最小值。

// 单位为分
console.log(randnum(500, 5000, 10, 10000))

// 第一轮结果
[ 516, 3317, 646, 515,  677, 636, 1861,  501, 518, 813 ]

// 第二轮结果
[ 724,  502,  500, 726, 2761, 2740, 500,  502,  522, 523 ]

// 第三轮结果
[ 500, 500, 1009, 899, 504, 4492, 500, 505,  551, 540 ]

第二组入参，均值靠近最大值，最小金额 5 元，最大金额 50 元，数量 10 个，总金额 400 元。均值 40 靠近最大值。

// 单位为分
console.log(randnum(500, 5000, 10, 40000))

// 第一轮结果
[ 4757, 4787, 3001, 1486, 4610, 4667, 4149, 4974, 2573, 4996 ]

// 第二轮结果
[ 4684, 2155, 3838, 4853, 4915, 3182, 4787, 3074, 4984, 3528 ]

// 第三轮结果
[ 4017, 4986, 3122, 4843, 4807, 4867, 2361, 3586, 3734, 3677 ]

从上面的实验结果可以看出，相同入参多次运行结果是不同的。如果均值靠近最小值或者最大值，结果可能分别会出现多个最小值和最大值，这个可以通过多次执行 smooth 函数来完全消除。

 

 

参考文献

[1] 漫画：如何实现抢红包算法？

[2] 微信拼手气红包背后的算法逻辑