详细理解中缀表达式并实现

Posted 2021-08-15 勇敢牛牛不怕困难@帅

中缀表达式的实现及概念

每日一笑：
公交车上，一丑女不小心踩了一个男人脚。男人大怒：你再踩一下试试，我让你好看！丑女大喜，急忙又踩了一脚道：太好了大哥，这下不用花钱整容了。

中缀表达式的定义

中缀表达式是一个通用的算术或逻辑公式表示方法。

中缀表达式就是我们通常所理解的数学公式或者是表达式例如：1+2/(1+1)+9*2类似这样简单的加减乘除运算的例子，我们称之为中缀表达式。
形如下图：

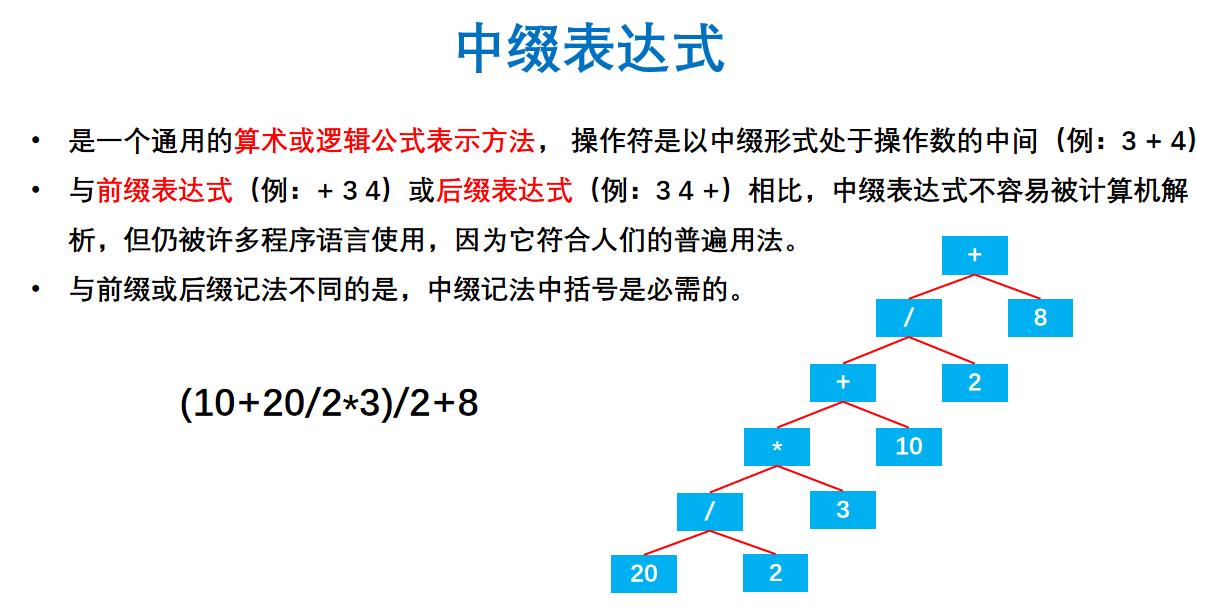
以人们的理解思路，便是以中缀形式去走的，更便于理解。但是计算机呢，大多数不是以中缀的方式去存与计算的，对于计算机来讲中缀表达式不便于理解。

中缀表达式的分解过程

例子：

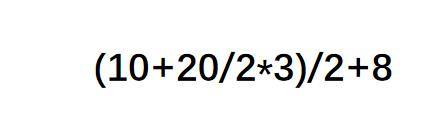
首先我们需要两个容器来分别存放数字类型和字符类型，在这里可以选择栈这一容器，栈是先进后出，后进先出的方式，刚好满足后到先处理，根据优先级判断。

第一步： 一个符号栈operatorStack，一个数字栈numberStack，刚开始栈都为空。

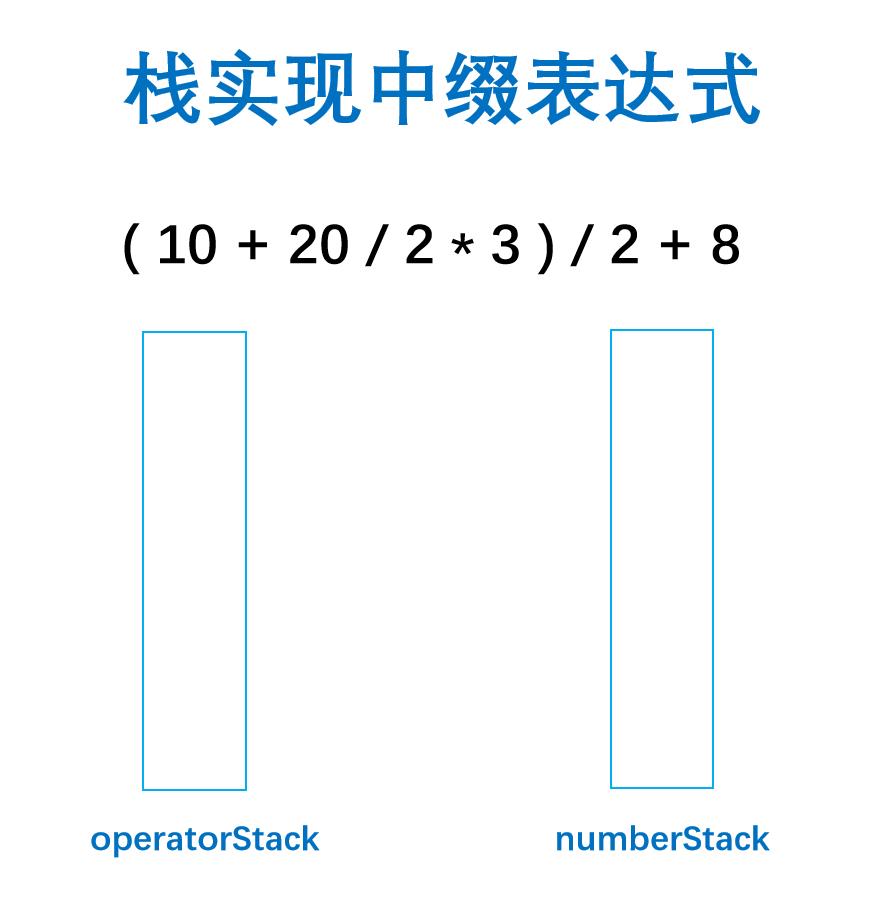
第二步： 识别表达式第一个字符的类型，是符号就入符号栈，如果是数值行就入数字栈，显然左括号是符号，就入符号栈；

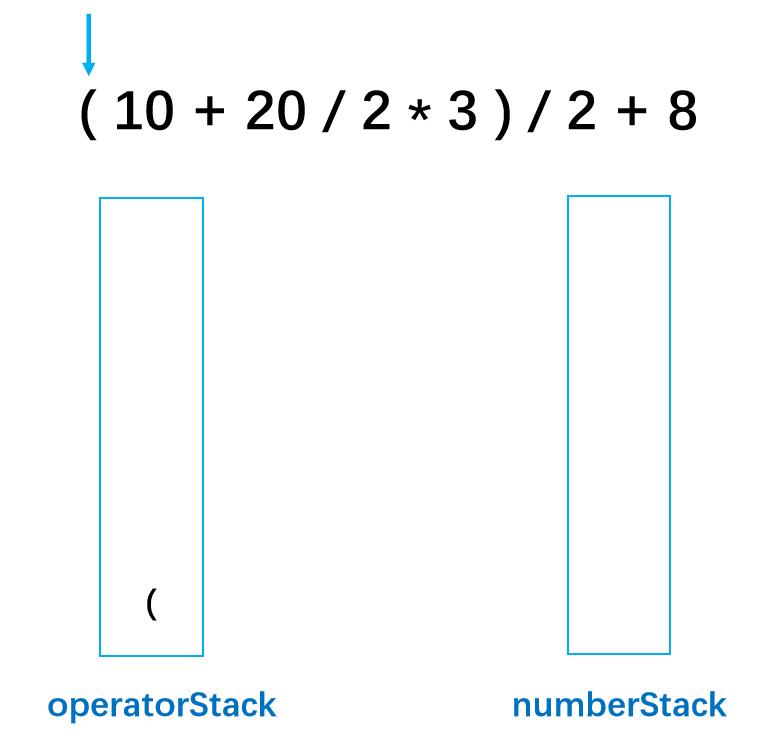
第三步： 接着循环下一位，判断出10为数值所以入数字栈。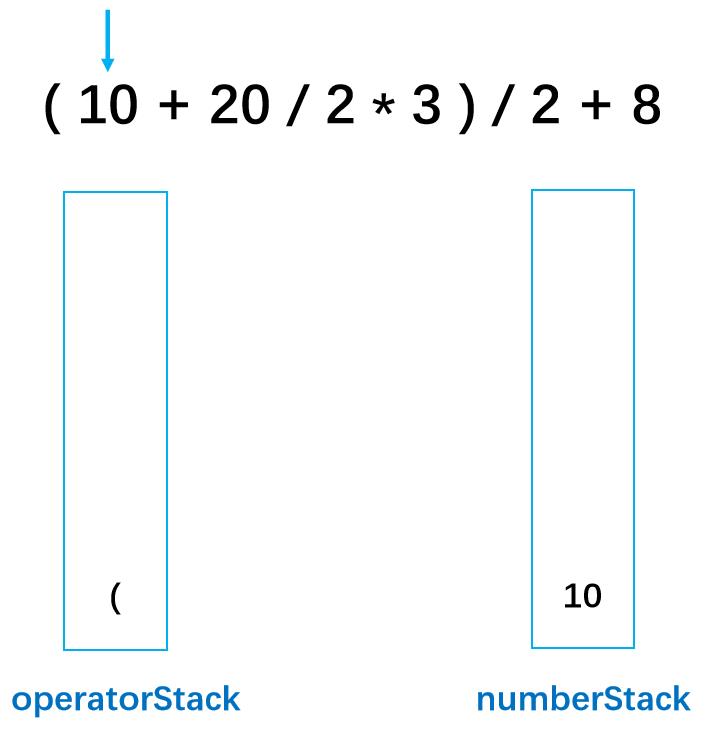
第四步： +号为字符，入字符栈

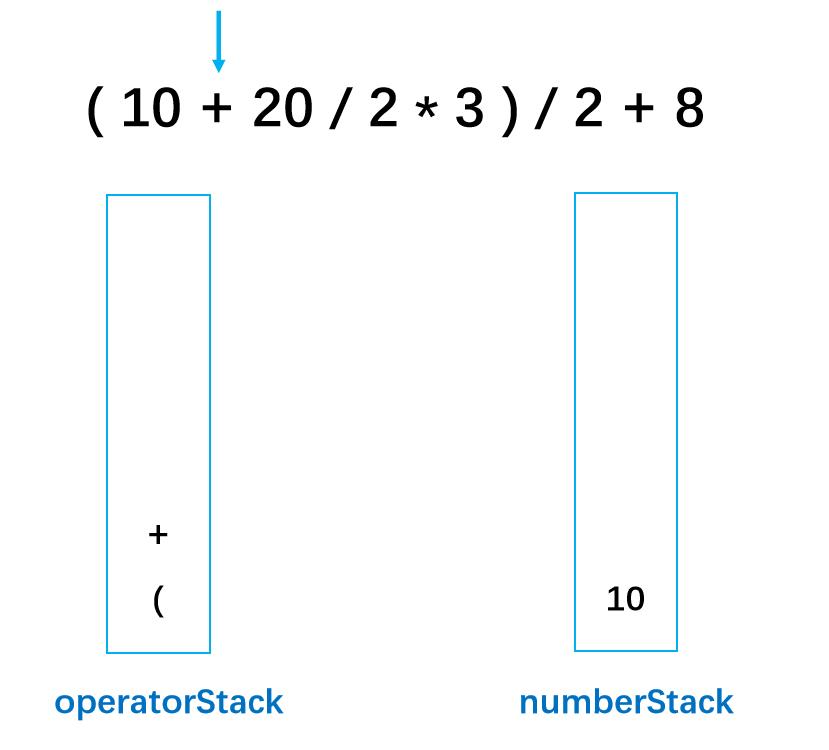
第五步： 20为数字，入数字栈

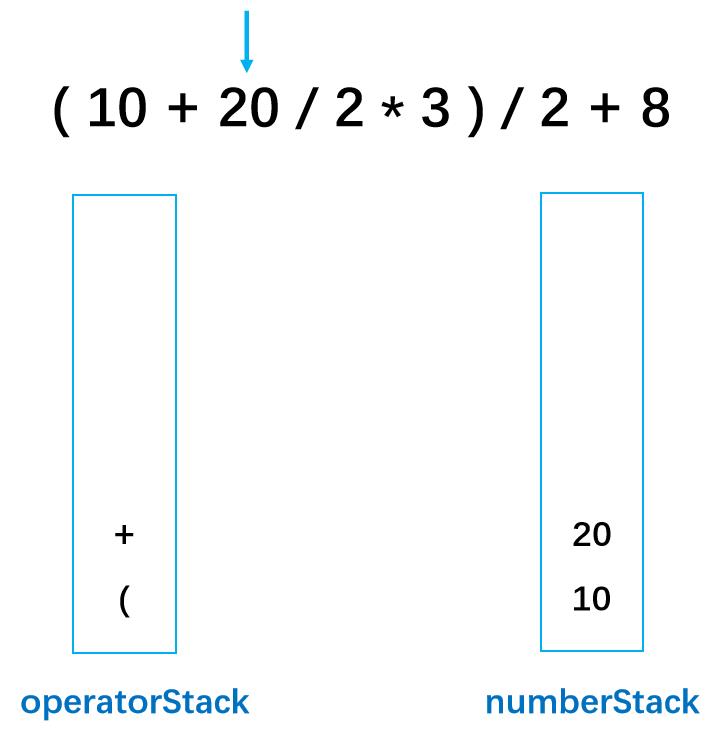
第六步： /为字符，入字符栈

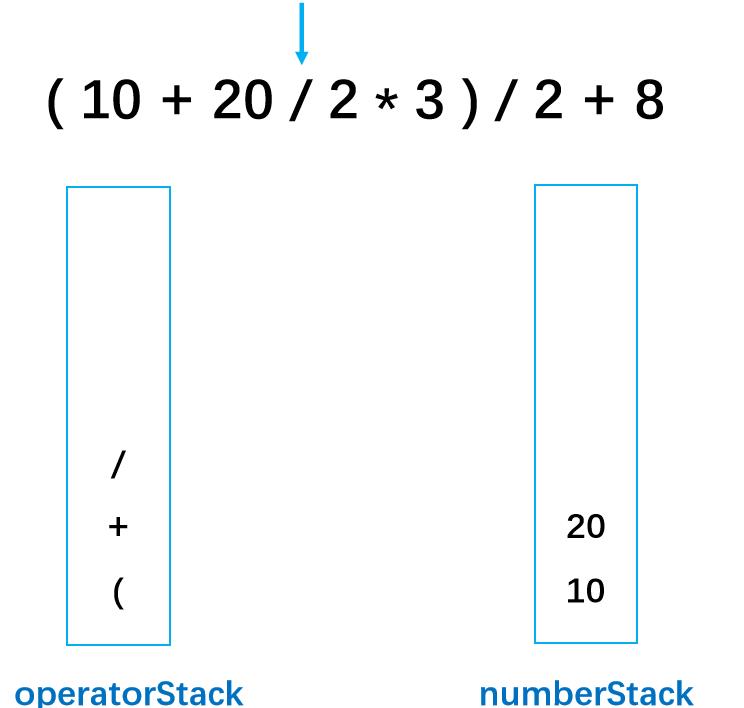
第七步： 2为数字，入数字栈

第八步： *为字符，入字符栈
但是，由于符号栈的栈顶元素为/，优先级和 ✖乘法的优先级相等，但是➗在✖乘号之前 所以要先进行运算，运算之后在入栈。数字栈弹两元素先弹出的作为除数，后弹出的作为被除数。运算结果存入数字栈中。

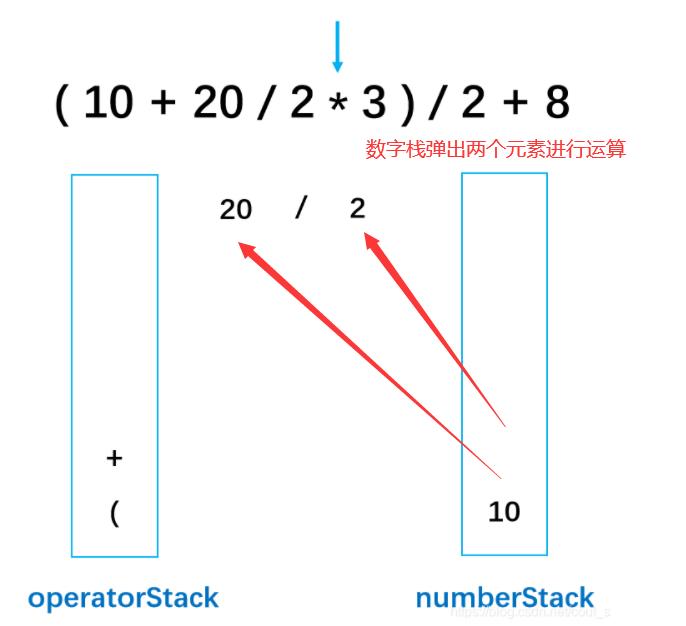
最后乘号入符号栈

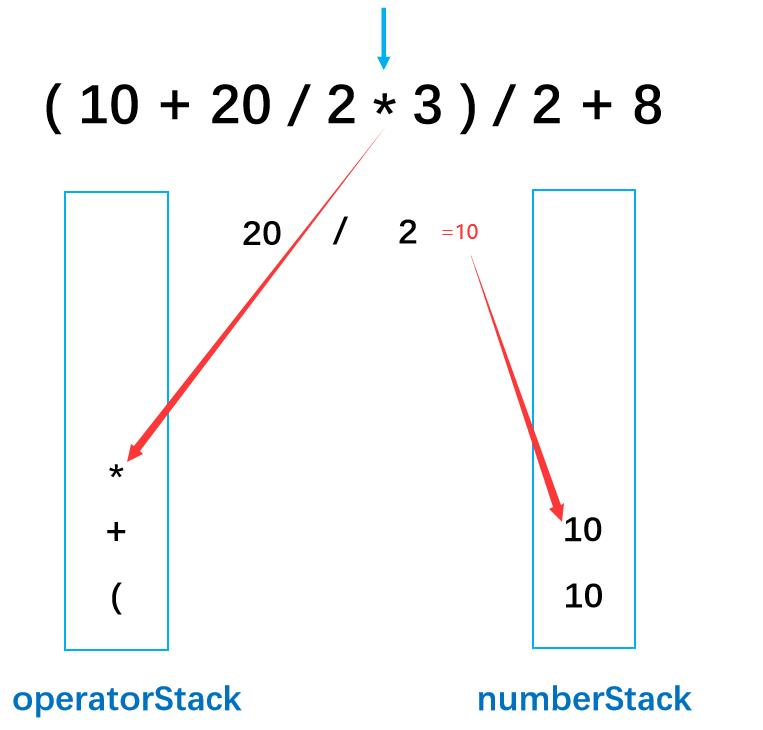
第九步： 3为数字，入数字栈

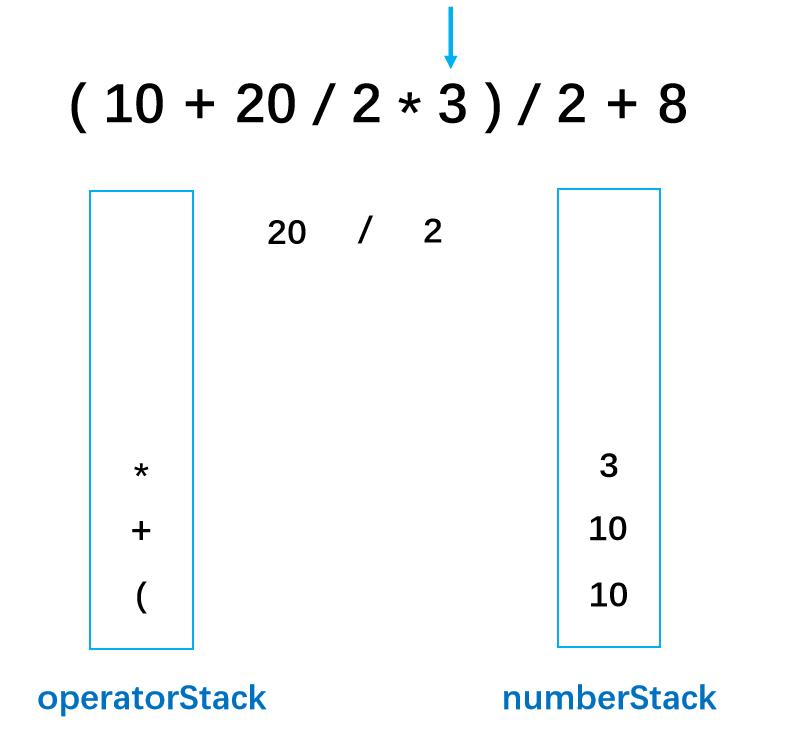
**第十步：**此时判断为右括号，就说明要将离右括号最近的左括号里面的数字要进行运算，运算结束之后 左括号弹栈，运算结果入栈。



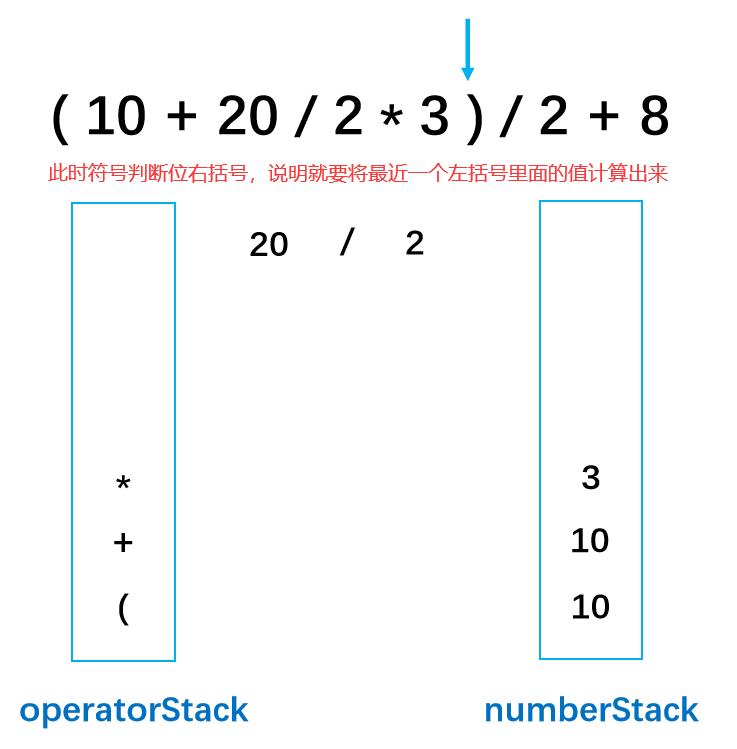
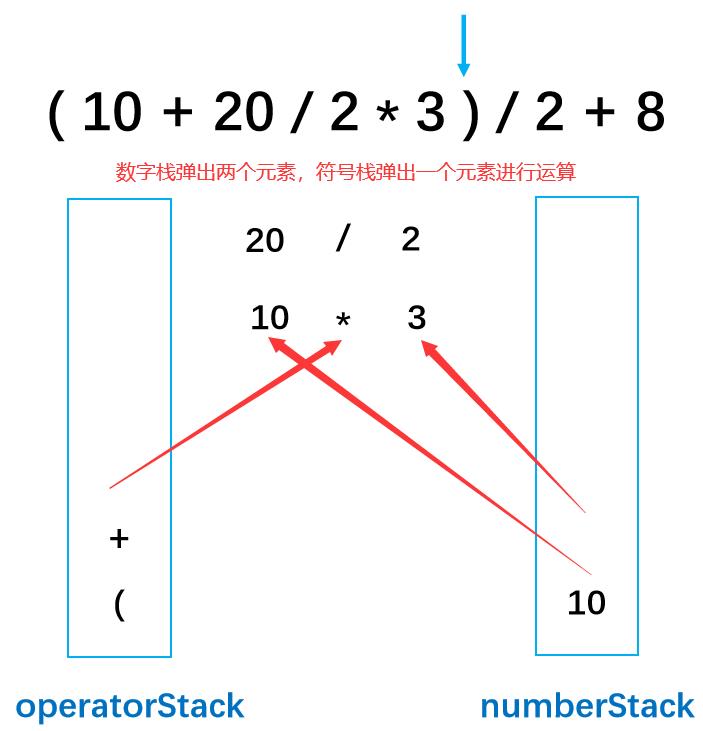
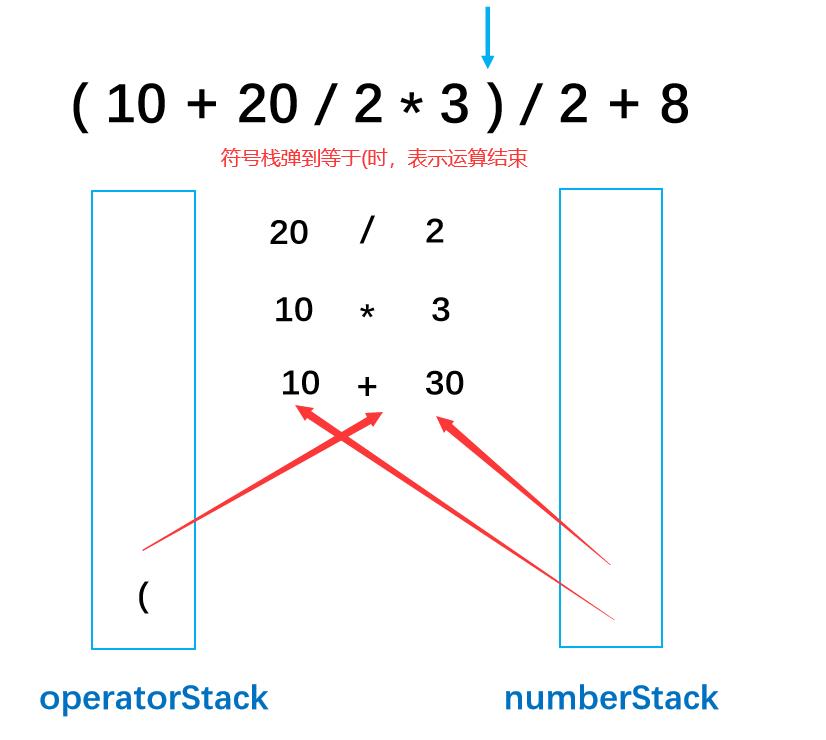
第十一步： /为符号，入符号栈

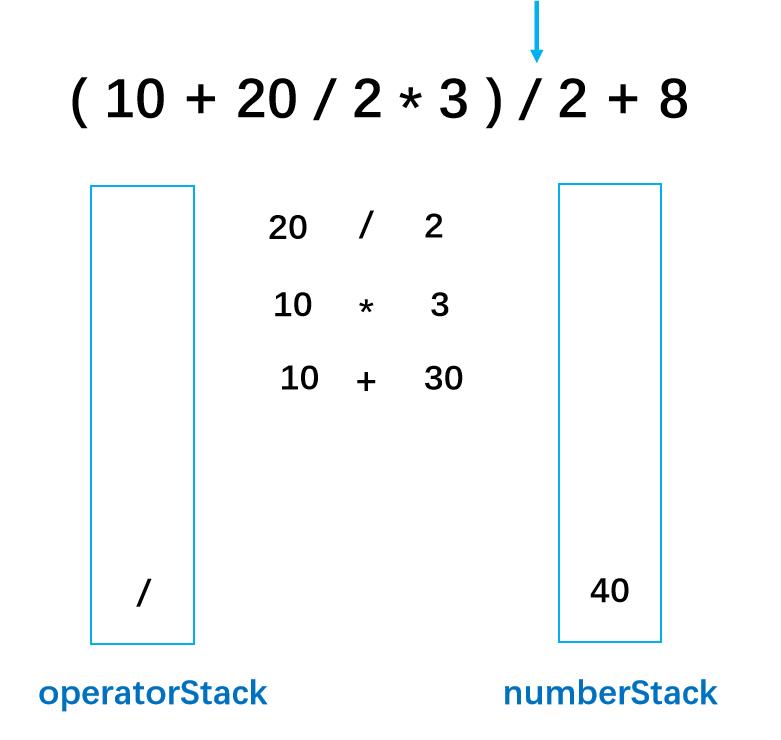
第十二步： 2为数字入数字栈

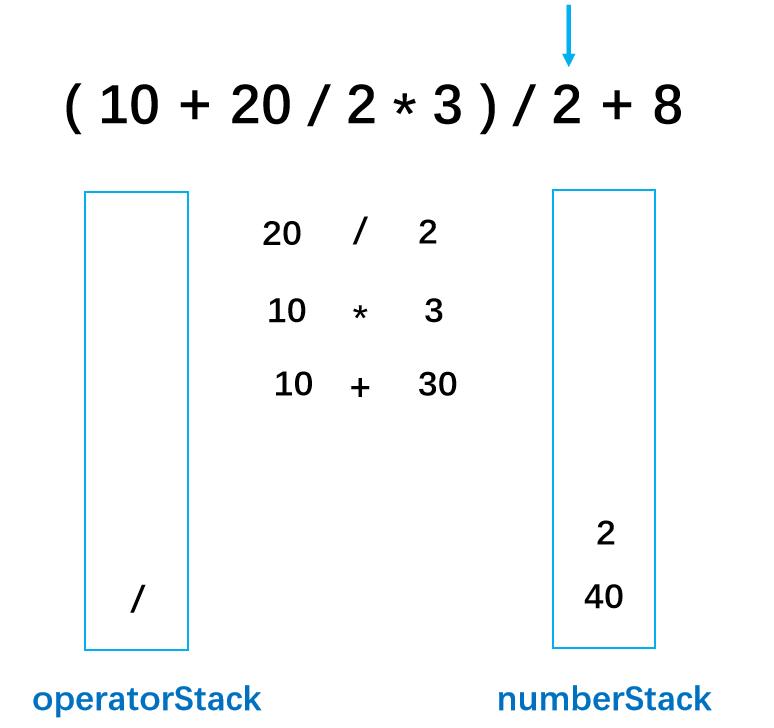
第十三步： 除法的优先级高于加法，所以优先处理除法运算。

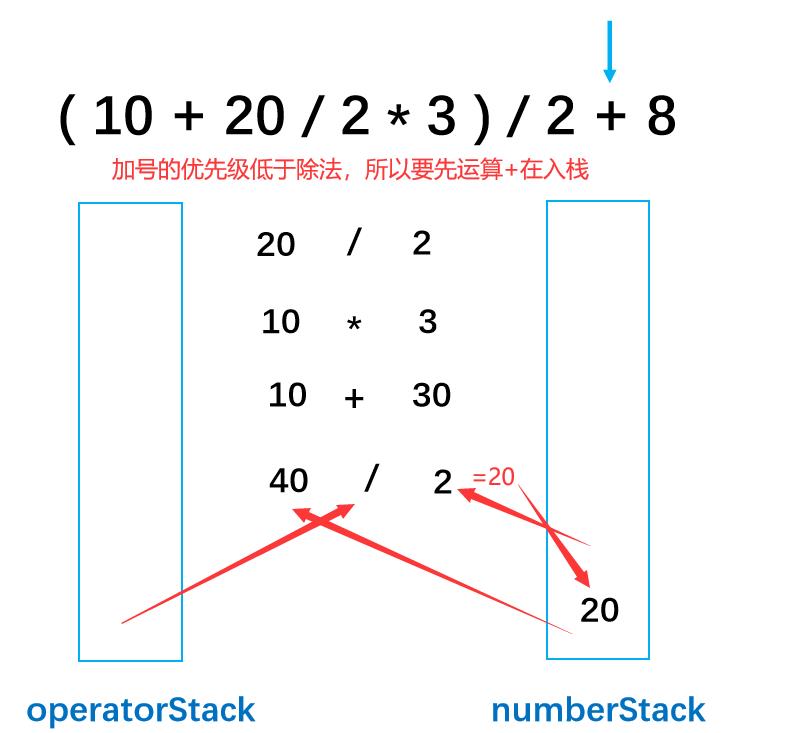
加法入符号栈

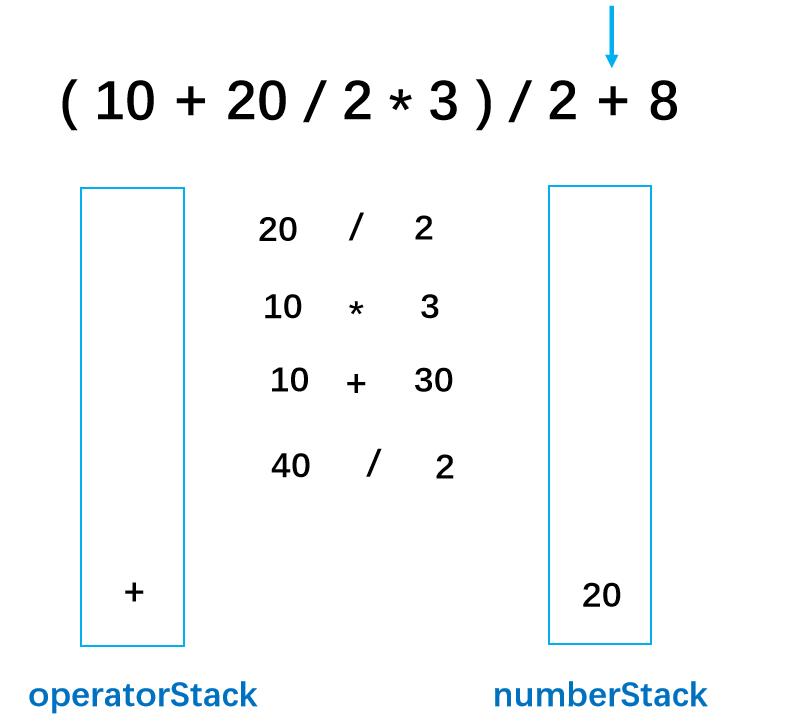
第十四步： 8为数字 进入数字栈，由于8为最后一个元素，所以要进行运算，将运算结果放入到数字栈中，此时的符号栈为空。

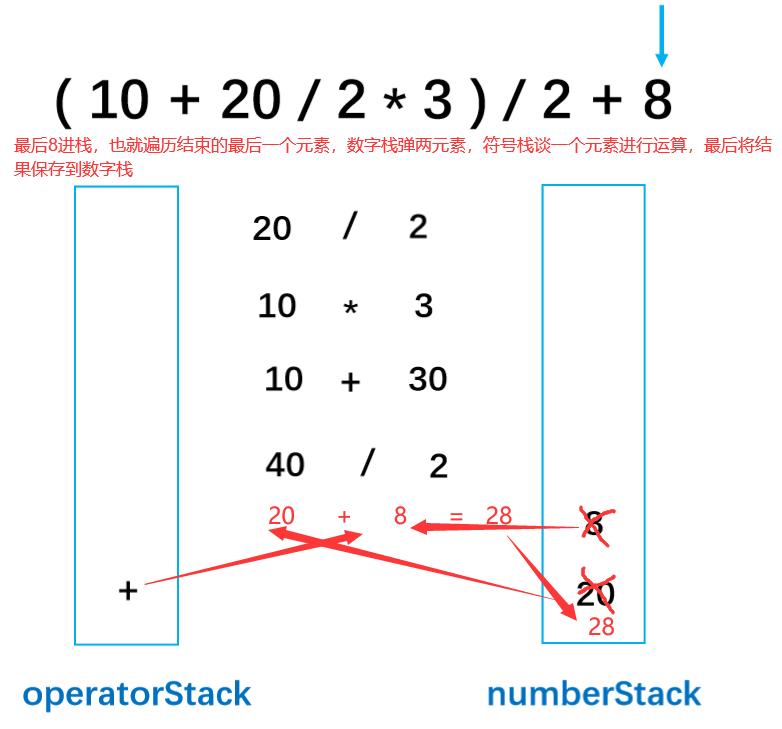
到这里中缀表达式的整个分解过程就结束了！，最后表达式的结果便是保存在数字栈中

接下来代码实现

package expression;

import java.util.Stack;

public class InfixExpression {//中缀表达式

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		String  expression = "(10+20/2*3)/2+8";
		int result = evaluteExpression(expression);
		System.out.println(result);
	}
	public static int evaluteExpression(String evaluteExpression) {
		Stack<Integer> numberStack = new Stack<>();//定义数字栈
		Stack<Character> operatorStack = new Stack<>();//定义符号栈
		evaluteExpression = formatExpression(evaluteExpression);//格式化
		String[] tokens = evaluteExpression.split(" ");//分割字符串为字符数组
		for(String token:tokens) {//遍历
			if(token.length()==0) {//如果字符数组为空直接跳过
				continue;
			}else if(token.charAt(0)=='(') {//为左括号直接入栈
				operatorStack.push('(');
			}else if(token.charAt(0)=='+'||token.charAt(0)=='-') {//为+或为-号时，都要处理符号栈里的元素
				while(!operatorStack.isEmpty()&&(operatorStack.peek()=='+'||operatorStack.peek()=='-'||
				operatorStack.peek()=='*'||operatorStack.peek()=='/')) {
					processAnOperator(operatorStack,numberStack);
				}
				operatorStack.push(token.charAt(0));
			}else if(token.charAt(0)=='*'||token.charAt(0)=='/') {//为*或为/号时，都要处理符号栈里*，/元素
				while(!operatorStack.isEmpty()&&(operatorStack.peek()=='*'||operatorStack.peek()=='/')) {
					processAnOperator(operatorStack,numberStack);
				}
				operatorStack.push(token.charAt(0));
			}else if(token.charAt(0)==')') {//为右括号时处理整个括号里的元素值
				while(operatorStack.peek()!='(') {
					processAnOperator(operatorStack,numberStack);
				}
				operatorStack.pop();
			}else {//为数值类型
				numberStack.push(new Integer(token));
			}	
		}
		while(!operatorStack.isEmpty()) {//直到符号栈不为空 一直处理
			processAnOperator(operatorStack,numberStack);
		}
		return numberStack.pop();
	}
	
	
	
	public static void processAnOperator(Stack<Character> operatorStack,Stack<Integer> numberStack) {//运算处理
		char ch = operatorStack.pop();
		int num1 = numberStack.pop();
		int num2 = numberStack.pop();
		switch(ch) {
		case '+':numberStack.push(num2+num1);break;
		case '-':numberStack.push(num2-num1);break;
		case '/':numberStack.push(num2/num1);break;
		case '*':numberStack.push(num2*num1);break;
		}
	}
	
	
	
	
	public static String formatExpression(String evaluteExpression ) {//格式化
		StringBuilder sb = new StringBuilder();
		for(int i=0;i<evaluteExpression.length();i++) {
			char c = evaluteExpression.charAt(i);
			if(c=='+'||c=='-'||
			c=='*'||c=='/'||
			 c=='('||c==')') {
				sb.append(' ');
				sb.append(c);
				sb.append(' ');
			}else {
				sb.append(c);
			}
			
		}
		
		return sb.toString();
	}

}

运行结果：

总结

对于中缀表达式，我们要明确两个观点 一个是需要两个栈来存储数字型元素和符号型元素，遇到符号时判断符号栈是否为空，为空直接入栈，不为空的前提下在判断运算符的优先级，在做处理。最后运算的结果保存在数字栈中，只需弹栈即可！