性能分析之排队论应用

Posted 2021-08-14 zuozewei

文章目录

• • 一、前言
  • 二、排队模型
  • • 1、M/M/1/∞ /∞ /FCFS：单线程单连接，先到先服务
    • 2、M/M/C/∞ /∞ /FCFS：多线程多连接，先到先服务
  • 三、排队的计算
  • • 1、排队计算 1
    • 2、排队计算 2
    • 3、排队计算 3
    • 4、小结
  • 四、数据统计分析
  • • 1、请求到达率
    • 2、响应时间分布
    • 3、小结
  • 五、创建 M/M/C/∞ /∞ /FCFS 模型
  • 六、总结

一、前言

之所以写排队论的话题是因为这个理论和性能分析中的队列分析有关。

这里我尽量不写和数学相关的公式，只写分析部分，以免看得人心塞。

写之前先说几个假设条件（在最后会对这几个条件加以说明）：

• 每请求的响应时间相同（为什么要做这个假设？是因为不想计算得太复杂）
• 每个服务器提供稳定的服务，没有抖动
• 到达分布是满足泊松分布的
• 响应时间分布是满足指数分布的

二、排队模型

1、M/M/1/∞ /∞ /FCFS：单线程单连接，先到先服务

（注：以上是 kendall 表达式）

在下图中有几个前提条件需要说明，单连接单服务进程。

如果这个连接中的前 8 个请求可以进入系统得到响应，并且同时还有两个空位，也就是说系统可以同时处理 10 个请求的话，那再接着到达系统的前两个请求就可以立即得到响应。那么后续的两个请求将进入队列等待。
这就是最简单的模型：M/M/1/∞ /∞ /FCFS。

2、M/M/C/∞ /∞ /FCFS：多线程多连接，先到先服务

（注：以上是 kendall 表达式）

当然大部分系统都不会是上面这个样子，而是下面这个样子。

在下图中，就是进来的连接通道有 4 个（有人问为什么是 4 个呢，是因为画多了太乱）。

如果每个连接中的前 8 个请求到达系统可以得到响应，后续两个也可以得到响应。那再后续的两个就必然进入队列等待。

这就是另一个模型：M/M/C/∞ /∞ /FCFS。

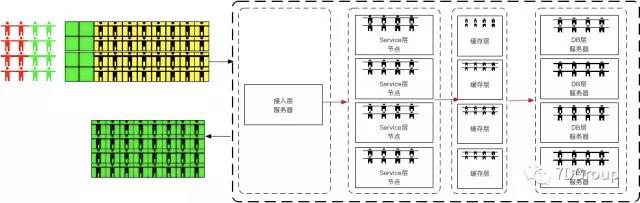
基于第二个模型标识下相应的数学符号：

三、排队的计算

代入相应的数据计算（因为数学公式实在是帖起来太费劲，并且看起来眼晕，这里我就直接把代入数据后的结果帖出来）。

1、排队计算 1

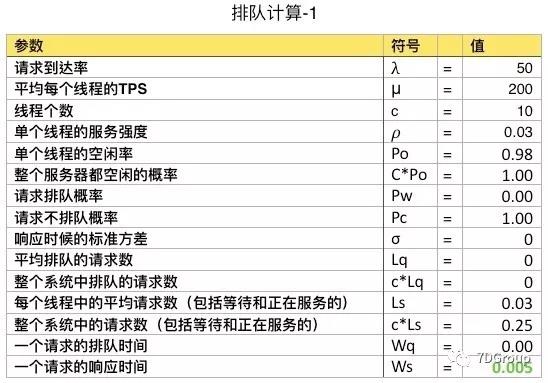
上表中有几个输入值，即 λ/μ/c，这几个值都是可以从系统中得到，或者测试出来的。下面的值部分是通过计算得来的。其中也有一个假设值就是标准方差，之所以现在的计算没有加入标准方差是想减少计算的复杂度。

2、排队计算 2

从上面的数据可以看到实际系统的处理能力是 2000请求/秒。那如果是 2000 请求同时到达系统会是什么样呢？如下所示：

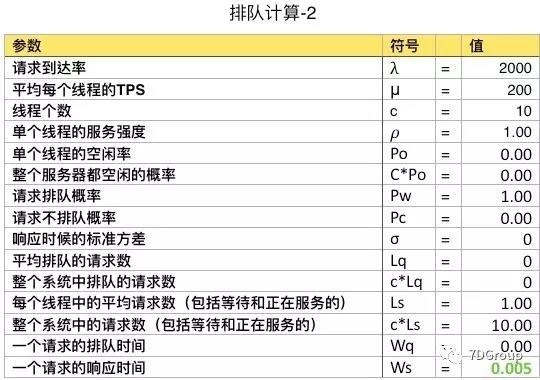
也就是说如果到达请求数和系统的能力一致的话，响应时间是不变的，但是服务强度、线程空闲率、新请求的排队概率、每线程的平均请求数等都变了。

3、排队计算 3

如果到达的请求数持续大于系统能力呢？如下所示：

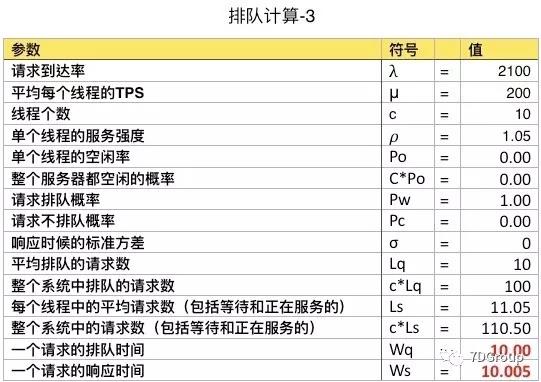
从上表可以看到，如果到达系统的请求数持续超过系统的处理能力的话，那将导致响应时间变长，并且都长在了排队中。

4、小结

通过排队的计算可以知道：

• 系统当前是否负载过重；

• 系统如果想满足更高的并发应该增加多少处理线程；

• 系统的超时应该如何设计；

• 系统的容量应该如何评估；

以上的计算过于理想化，在现实的环境中当然不会是这样的结果，所以本文的标题是简述。

在现实的环境计算中，有几个点是需要再细究的（对应开篇的假设条件）。

• 到达率：通过系统中的请求到达时间点统计之后，通过卡方检验判断到达率满足哪种分布模型；
• 响应时间的标准方差：通过统计响应时间，计算标准方差后代入计算，则响应时间也会受到影响；
• 系统的处理能力：在系统有峰值持续时间对响应时间和超时设计的要求；

对这些做细致的统计分析之后，才能对一个系统容量有比较好的指导作用。

四、数据统计分析

今天就说明两个重要的输入数据的获取和分布说明。

这里以一个示例来说明一下，在 7D Group 的 server上 搭了一个简单的应用，我用 jmeter 做了一个最简单的脚本，一个 get 就结束。

如果想分析更复杂的系统，可以将整个业务流做为分析对象，粒度的选取对分析的结果会有影响，所以要确定自己的分析目标。

1、请求到达率

通过 nginx 的日志（用 tomcat 的日志也可以）分析得到如下到达时间分布和频率如下：

单位：s

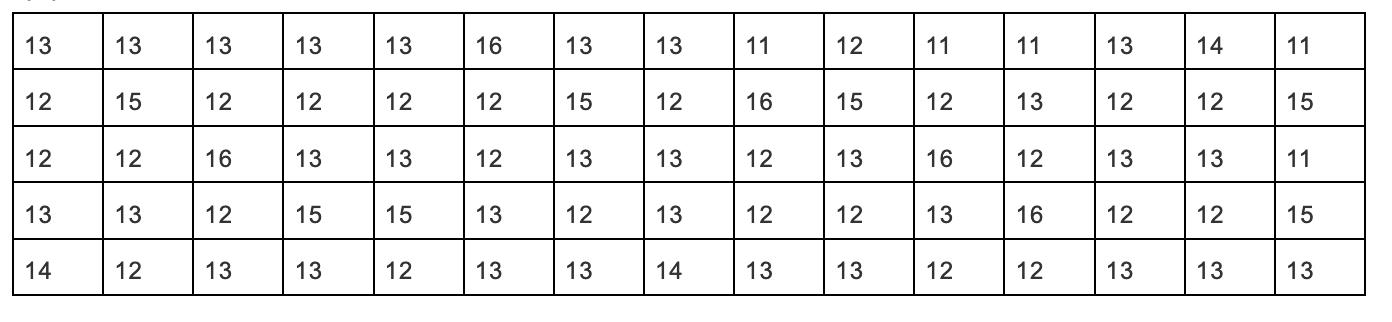
通过 K-S 检验结果如下：

可见到达分布是符合泊松分布的。

2、响应时间分布

通过 nginx 的日志（用 tomcat 的日志也可以）分析得到如下响应时间如下表所示：

单位：ms


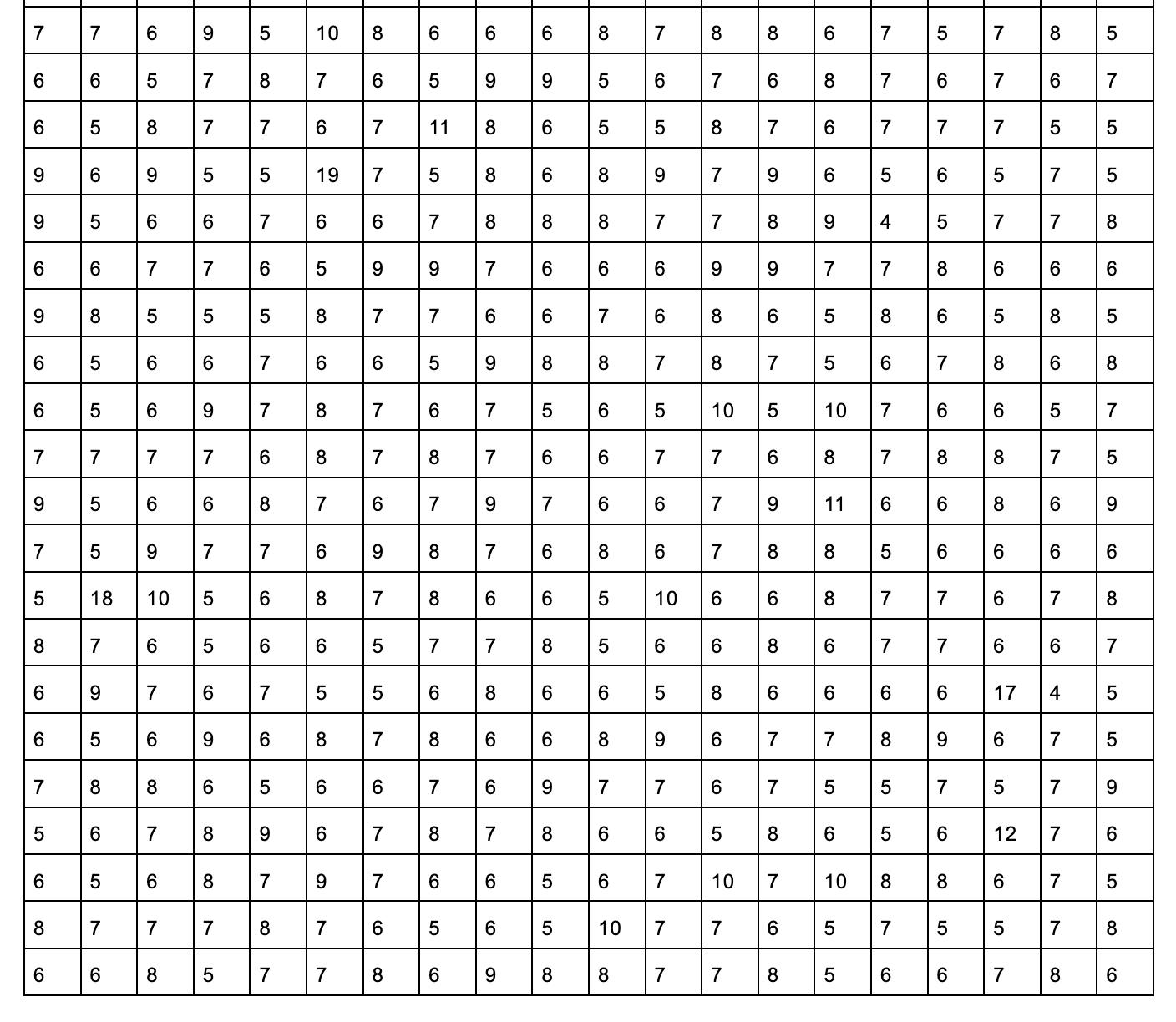
通过 K-S 检验结果如下：

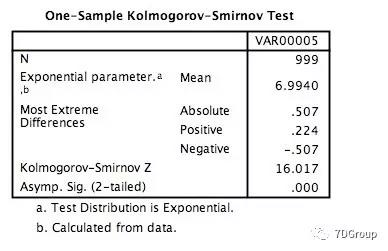
可见响应时间是符合指数分布的。

这两个数据满足了 M/M/C/∞ /∞ /FCFS 的条件，接下来就可以用这个模型的相应计算方法来计算了。

对其他的排队模型也是一样需要分析模型的前提条件。所以对实际数据的分析就非常重要。

3、小结

要创建一个成型的排队模型，有到达率和响应时间分析是不够的，还需要几个数据：

• 设定到达率随机数种子，以确定生成的随机数可重复且要满足真实的分布，不然模型不可复用；

• 确定队列长度和等待时间；

• 确定有几个串行队列和并行服务器；

当我们面对一个更复杂的系统时，也一定不要慌乱，数据分析是一个理智的过程。

五、创建 M/M/C/∞ /∞ /FCFS 模型

本文使用这个模型，因为这个是比较典型的排队场景，在性能的场景中经常可以遇到。

定义如下参数：

set.seed(2)   # 定义随机数种子，以保证随机数据具有可重复性
Requests<- 1000000  #请求数
ArrivalRate <- 1/2   #到达率
SeviceRate <- 1/3   #服务率
Threads = 10 # 定义线程个数

通过一些计算，得到一些中间数据：

interarrivals <- rexp(Requests, ArrivalRate)   #请求分布
arrivals <- cumsum(interarrivals)              #请求总数
service <- rexp(Requests, SeviceRate)          #请求得到的服务分布
rho <- (1/SeviceRate) / (1/ArrivalRate)         #服务强度
Vectorize(P_n, "n")(rho=rho, n=c(0:30), k = k)  #向量化转化

通过排队模型计算得如下结果（算法请参考排队论相关书籍，只要用语言实现即可，本文用 R 语言示例，只要知道算法，用 excel也是可以的）：

系统内的响应时间：
# Mean response time (time in system)
[1] 2.500001

请求平均响应时间：
# Mean response time
[1] 2.996585

六、总结

在创建模型时，需要将相关的参数考虑进来，以确定对模型的影响。

不管是在宏观分析，还是在微观分析上，只要思路清晰，都可以用排队论来分析性能，前提是要理解如何用。不要乱用。

前面提到了一些基本的概念和数据获取及分布分析，这些都是有成型的工具可以完成，像 SPSS 就可以完成卡方检验或 K-S 检验，以确定数据是否是泊松分布或指数分布。因为确定了分布之后，才可以用相应的排队论表达式和公式来完成后面的计算。

系统数据有些比较规整（比如说一般分布的马尔可夫到达链），有些比较复杂（各种不同的分布模型）。需要对这些都进行了分析之后，才能创建出适合的模型出来。所以抓取一些数据做统计分析就非常重要了。

我的目的是通过这样的计算可以得到比较通用的模型（不是绝对能用哦），在不同的场景下都可以通过得到一些基本的数据信息之后，加以整理分析，就可以得到可以复用的排队模型，并最终指导生产运营的推导需求。

这样就可以避免部分在生产环境上的问题，不用花大量的时间成本去做分析，即可知道要加多少服务器，要支持多少个用户，用户的响应时间变化曲线等等。