P1224 [NOI2013] 向量内积(矩阵乘法&随机化)

Posted 2021-08-14 Harris-H

P1224 [NOI2013] 向量内积(矩阵乘法&随机化)

当$k=2$时

考虑维护前$i-1$个向量的前缀和。

将其与第$i$个向量进行求内积，若不等于$k-1$，则必然存在第$i$项与其内积为$0$满足条件，然后就暴力找即可。

每次特判的复杂度是$O(d)$的，若找到了必定在$O(nd)$的范围内可以找到。

若$k=3$时，考虑$1^2\equiv 2^2(\mathrm{m}\mathrm{o}\mathrm{d}3)$

则我们可以维护$c[i][j]=\sum _{j=1}^{i-1}{a}_{jx}{a}_{jy}$

因为$(\sum _{k=1}^d{a}_{ik}{a}_{jk}{)}^2=\sum _{k_1}^d\sum _{k_2}^d{a}_{i{k}_1}{a}_{j{k}_1}{a}_{i{k}_2}{a}_{j{k}_2}$

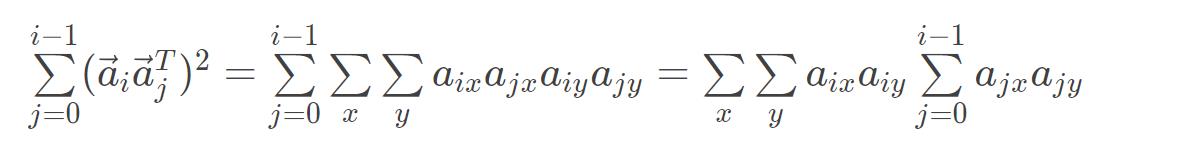
所以维护一个$c[i][j]$的前缀和即可。

每次随机化一下$id$，减少失败概率。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll; 
const int N=101000,M=111,inf=0x3f3f3f3f,mod=1e9+7;
#define mst(a,b) memset(a,b,sizeof a)
#define rg register
inline int read(){
	int res=0;
	char ch=getchar(),ch1=ch;
	while(!isdigit(ch))ch1=ch,ch=getchar();
	while(isdigit(ch))
		res=(res<<3)+(res<<1)+ch-'0',ch=getchar();
	return ch1=='-'?-res:res;
}
int a[N][M],b[M],c[M][M];
int n,mo,d;
inline bool ck(int x,int y){
	int s=0;
	for(rg int i=1;i<=d;i++) s+=a[x][i]*a[y][i];
	return s%mo; 
}
inline int f(int x){
	int s=0;
	if(mo==2){
		for(rg int i=1;i<=d;b[i]^=a[x][i],++i)
			s^=a[x][i]&b[i];
	}
	else {
		for(rg int i=1;i<=d;i++)
			for(rg int j=1;j<=d;c[i][j]+=a[x][i]*a[x][j],j++)
				s+=a[x][i]*a[x][j]*c[i][j]%mo;
	}
	return s%mo;
}
int id[N];
int main(){
	n=read(),d=read(),mo=read();
	for(rg int i=1;i<=n;++i){
		id[i]=i;
		for(rg int j=1;j<=d;++j)
			a[i][j]=read()%mo;
	}
	for(rg int T=0;T<6;T++){
		mo==2?mst(b,0):mst(c,0);
		random_shuffle(id+1,id+n+1);
		for(rg int i=1;i<=n;++i)
			if(f(id[i])!=(i-1)%mo)
				for(rg int j=1;j<i;++j){
					if(!ck(id[i],id[j])){
						if(id[i]>id[j]) swap(i,j);
						return printf("%d %d\\n",id[i],id[j]),0;
					}
				}
	}
	puts("-1 -1");
	return 0;
}