并查集原理分析

Posted 2021-08-14 ych9527

文章目录

• 1.并查集是什么
• 2.并查集性质
• 3.并查集可以解决的问题
• 4.并查集模板
• 5.并查集的应用

1.并查集是什么

• 在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时**，每个元素自成一个单元素集合**，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集

2.并查集性质

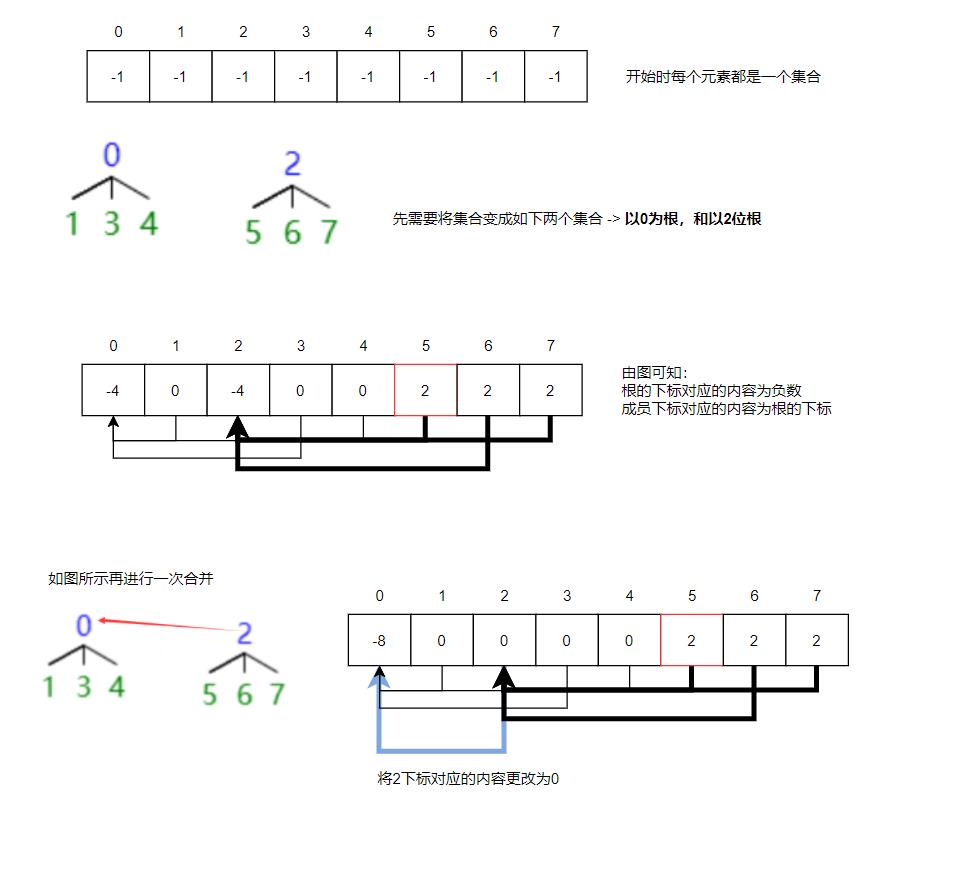
• 由上图可知，并查集有如下几点性质
  • 数组下标对应集合中元素的编号
  • 根下标对应的内容为负数
  • 子元素下标对应的内容为根的下标(子元素下标对应的内容非负数)

3.并查集可以解决的问题

• 查找元素属于哪个集合
  • 查找对应元素的根
• 查看两个元素是否属于同一个集合
  • 判断两个元素的根是否相等
• 将两个集合归并成一个集合
  • 将两个元素的根进行合并
• 集合的个数
  • 查找根的个数

4.并查集模板

#include "test.h"

class UnionFindSet
{
public:
	UnionFindSet(int size)//传入元素的个数
	{
		_arr.resize(size, -1);
	}

	int FindRoot(int x)//给定一个下标寻找它的根
	{

		while (_arr[x] >= 0)//大于等于0，表示里面存储的是根的下标
		{
			x = _arr[x];
		}
		return x;
	}

	bool Union(int x1, int x2)//将两个下标对应的根，进行合并
	{
		//找到两个根的位置
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		
		if (root1 == root2)
			return false;

		_arr[root1] += _arr[root2];
		_arr[root2] = root1;

		return true;
	}

private:
	vector<int> _arr;
};

5.并查集的应用

省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。返回矩阵中 省份 的数量。

题解：

• 典型的并查集题目
• 首先每个为1的城市，本身都是一颗树，但是他们记录的下标表示两个城市相连，即将这两颗树相连
• 最后统计并查集中根的数量，返回即可 -> 根的数量就是省的数量

class Solution {
public:

class UnionFindSet
{
public:
	UnionFindSet(int size)
	{
		_arr.resize(size, -1);
	}

	int FindRoot(int x)//给定一个下标寻找它的根
	{
		while (_arr[x] >= 0)//大于等于0，表示里面存储的是根的下标
		{
			x = _arr[x];
		}
		return x;
	}

	bool Union(int x1, int x2)//将两个下标对应的根，进行合并
	{
		//找到两个根的位置
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		
		if (root1 == root2)
			return false;

		_arr[root1] += _arr[root2];
		_arr[root2] = root1;

		return true;
	}

    int Size()
    {
        int n=0;
        for(auto&e:_arr)
        {
            if(e<0)//为根
            n++;
        }
        return n;
    }

private:
	vector<int> _arr;
};
    int findCircleNum(vector<vector<int>>& isConnected) {
        UnionFindSet uft(isConnected.size());

        for(int i=0;i<isConnected.size();i++)
        {
            for(int j=0;j<isConnected.size();j++)
            {
                if(isConnected[i][j]==1)
                {
                    uft.Union(i,j);
                }
            }
        }

        return uft.Size();
    }
};

等式方程的可满足性

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：“a==b” 或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

题解：

• 如果两个字符相等，则放入同一个集合之中 -> 即他们的根相同
• 如果两个字符不相等，则去集合之中查找他们的根 -> 根相同则返回false

class Solution {
public:
    class UnionFindSet
    {
    private:
        vector<int> arr;
    public:
        UnionFindSet(int n)
        {
            arr.resize(n,-1);
        }

        int FindRoot(int x)//寻找根
        {
            while(arr[x]>=0)//表示不是根
            {
                x=arr[x];
            }
            return x;
        }

        bool Union(int x,int y)
        {
            int root1=FindRoot(x);
            int root2=FindRoot(y);
            if(root1==root2)
            return false;

            arr[root1]+=arr[root2];
            arr[root2]=root1;
            return true;
        }
    };
    bool equationsPossible(vector<string>& equations) {
        //将相等的都放入一个集合之中
        //然后判断不相等的在不在一个集合-> 根相不相同

        UnionFindSet ufs(26);

        for(auto&e:equations)
        {
            if(e[1]=='=')
            ufs.Union(e[0]-'a',e[3]-'a');
        }
        for(auto&e:equations)
        {
            if(e[1]!='=')
            {
                int root1=ufs.FindRoot(e[0]-'a');
                int root2=ufs.FindRoot(e[3]-'a');
                if(root1==root2)
                    return false;
            }
        }
      return true;
    }
};