优化求解t-分布扰动策略和变异策略的花授粉算法matlab源码

Posted 2021-08-14 博主企鹅号1575304183

一、花朵授粉算法

花朵授粉算法（ Flower Pollination Algorithm，FPA）是由英国剑桥大学学者Yang于2012年提出的，其基本思想来源于对自然界花朵自花授粉、异花授粉的模拟，是一种新的元启发式群智能随机优化技术 。算法中为了简便计算，假设每个植物仅有一朵花，每朵花只有一个配子，我们可以认为每一个配子都是解空间中的一个候选解。

Yang通过对花朵授粉的研究，抽象出以下四大规则：

1） 生物异花授粉被考虑为算法的全局探测行为，并由传粉者通过Levy飞行的机制实现全局授粉；

2）非生物自花授粉被视作算法的局部开采行为，或称局部授粉；

3）花朵的常性可以被认为是繁衍概率，他与两朵参与授粉花朵的相似性成正比例关系；

4）花朵的全局授粉与局部授粉通过转换概率 p∈[０，１]进行调节。 由于物理上的邻近性和风等因素的影响，在整个授粉活动中，转换概率 p是一个非常重要的参数。 文献[１]中对该参数的试验研究认为，取 p =０.８ 更利于算法寻优。

直接上步骤（以多元函数寻优为例）：

目标函数 ： min g = f(x1,x2,x3,x4...........xd)

设置参量：N（候选解的个数），iter（最大迭代次数），p（转换概率），lamda（Levy飞行参数）

初始化花朵，随机设置一个NXd的矩阵；

计算适应度，即函数值；

获取最优解和最优解得位置；

A循环 1 ： 1 ：iter

    B循环

        if rand < p

            全局授粉；

        else

            局部授粉；

        end if

        更新新一代的花朵与适应度（函数变量和函数值）；

    B循环end

    获取新一代的最优解与最优解位置；

A循环end

全局更新公式：xi(t+1) = xi(t) + L(xi(t) - xbest(t))    L服从Levy分布，具体可以搜索布谷鸟算法。

局部更新公式：xi(t+1) = xi(t) + m(xj(t) - xk(t))    m是服从在[0,1]上均匀分布的随机数。其中，xj和xk是两个不同的个体

二、t-分布扰动策略和变异策略的花授粉算法

（1）混沌映射初始化花朵个体位置

 （2）基于t-分布扰动策略的全局搜索

（3）基于变异策略的局部搜索 

 （4）算法实现

 

二、演示代码

%__________________________________________
% fobj = @YourCostFunction
% dim = number of your variables
% Max_iteration = maximum number of generations
% SearchAgents_no = number of search agents
% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n
% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n
% If all the variables have equal lower bound you can just
% define lb and ub as two single number numbers

% To run ALO: [Best_score,Best_pos,cg_curve]=ALO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)

% The Whale Optimization Algorithm
function [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj,handles,value)

% initialize position vector and score for the leader
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems


%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iter);

t=0;% Loop counter

% Main loop
while t<Max_iter
    for i=1:size(Positions,1)
        
        % Return back the search agents that go beyond the boundaries of the search space
        Flag4ub=Positions(i,:)>ub;
        Flag4lb=Positions(i,:)<lb;
        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        
        % Calculate objective function for each search agent
        fitness=fobj(Positions(i,:));
        All_fitness(1,i)=fitness;
        
        % Update the leader
        if fitness<Leader_score % Change this to > for maximization problem
            Leader_score=fitness; % Update alpha
            Leader_pos=Positions(i,:);
        end
        
    end
    
    a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)
    
    % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)
    a2=-1+t*((-1)/Max_iter);
    
    % Update the Position of search agents 
    for i=1:size(Positions,1)
        r1=rand(); % r1 is a random number in [0,1]
        r2=rand(); % r2 is a random number in [0,1]
        
        A=2*a*r1-a;  % Eq. (2.3) in the paper
        C=2*r2;      % Eq. (2.4) in the paper
        
        
        b=1;               %  parameters in Eq. (2.5)
        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)
        
        p = rand();        % p in Eq. (2.6)
        
        for j=1:size(Positions,2)
            
            if p<0.5   
                if abs(A)>=1
                    rand_leader_index = floor(SearchAgents_no*rand()+1);
                    X_rand = Positions(rand_leader_index, :);
                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)
                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)
                    
                elseif abs(A)<1
                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)
                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)
                end
                
            elseif p>=0.5
              
                distance2Leader=abs(Leader_pos(j)-Positions(i,j));
                % Eq. (2.5)
                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);
                
            end
            
        end
    end
    
    t=t+1;
    Convergence_curve(t)=Leader_score;
    
    if t>2
        line([t-1 t], [Convergence_curve(t-1) Convergence_curve(t)],'Color','b')
        xlabel('Iteration');
        ylabel('Best score obtained so far');        
        drawnow
    end
 
    
    set(handles.itertext,'String', ['The current iteration is ', num2str(t)])
    set(handles.optimumtext,'String', ['The current optimal value is ', num2str(Leader_score)])
    if value==1
        hold on
        scatter(t*ones(1,SearchAgents_no),All_fitness,'.','k')
    end
    
    
    
    
end

四、仿真结果

表1 测试函数基本信息

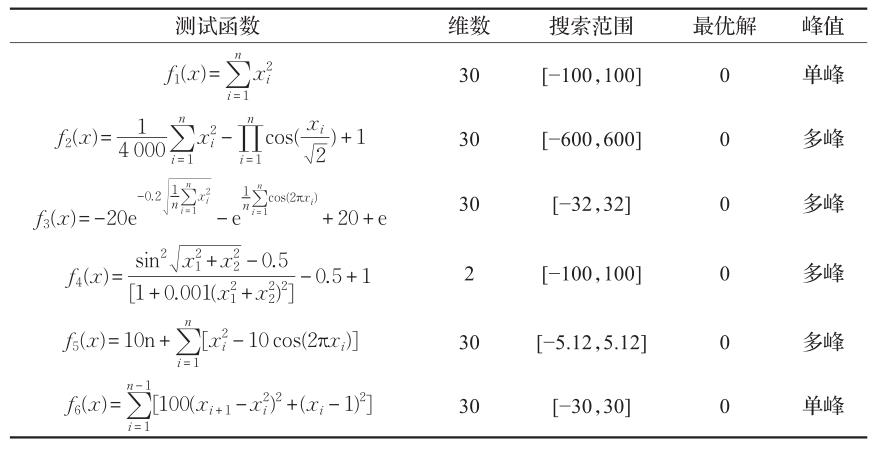
为了验证本文提出的tMFPA算法的性能，仿真实验的每种算法独立运行30次，最大迭代次数设为2000次，以30维为例。
结果显示如下：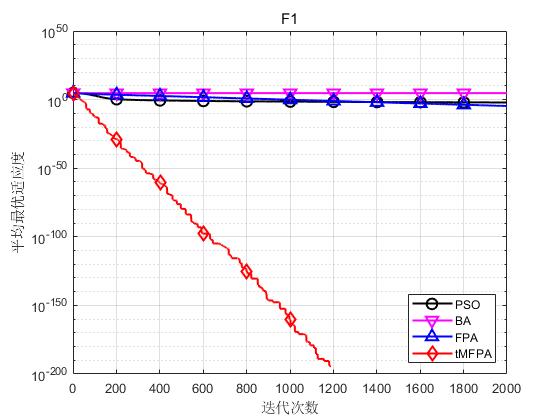

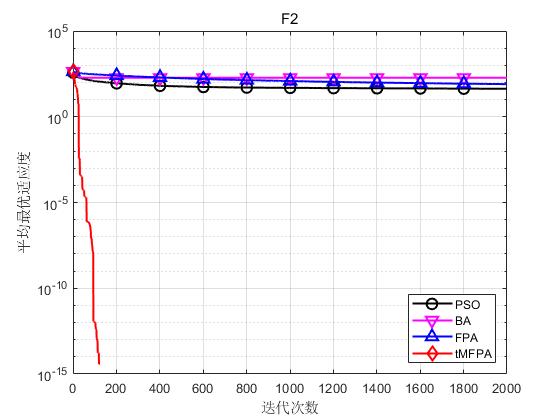
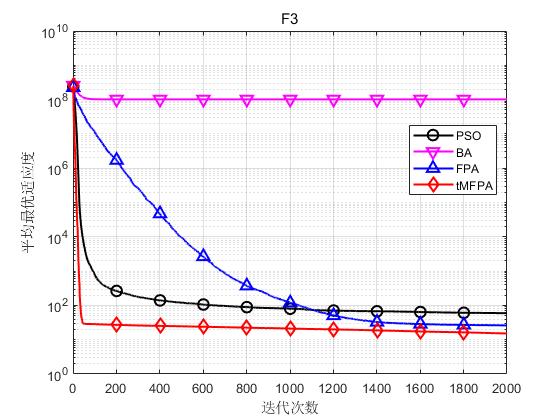
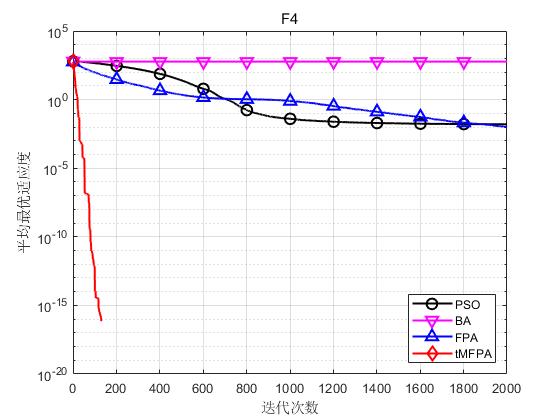
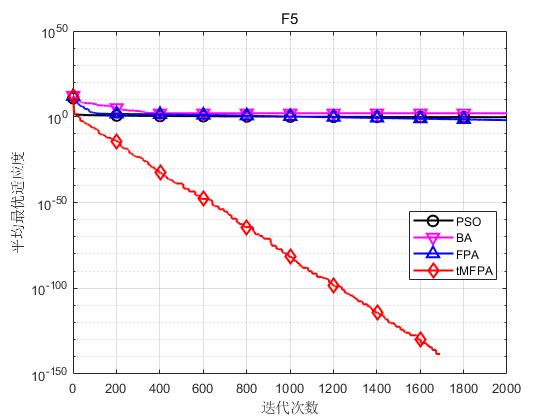
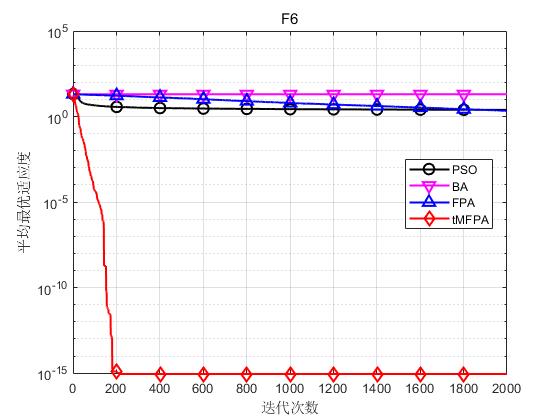
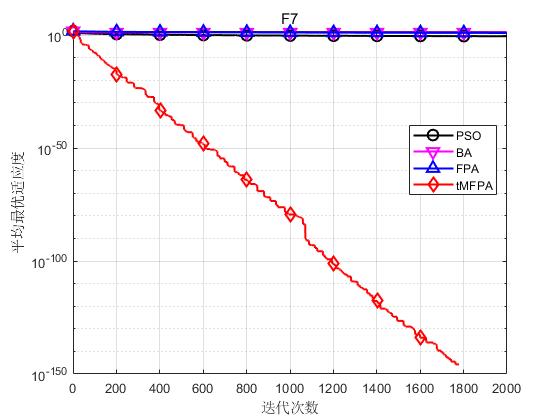
结果表明，tMFPA相比于FPA和其他启发式智能算法具有更好的寻优精度和收敛速度。 

五、参考文献及代码私信博主

[1] 宁杰琼,何庆. t-分布扰动策略和变异策略的花授粉算法[J]. 小型微型计算机系统, 2021, 42(1): 64-70.