优化求解基于麻雀算法优化PID参数matlab源码

Posted 2021-08-14 博主企鹅号1575304183

一、PID控制简介

   PID( Proportional Integral Derivative)控制是最早发展起来的控制策略之一，由于其算法简单、鲁棒性好和可靠性高，被广泛应用于工业过程控制，尤其适用于可建立精确数学模型的确定性控制系统。

   在工程实际中，应用最为广泛的调节器控制规律为比例、积分、微分控制，简称PID控制，又称PID调节，它实际上是一种算法。PID控制器问世至今已有近70年历史，它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，控制理论的其它技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象，或不能通过有效的测量手段来获得系统参数时，最适合用PID控制技术。PID控制，实际中也有PI和PD控制。PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。

   从信号变换的角度而言，超前校正、滞后校正、滞后－超前校正可以总结为比例、积分、微分三种运算及其组合。

   PID调节器的适用范围：PID调节控制是一个传统控制方法，它适用于温度、压力、流量、液位等几乎所有现场，不同的现场，仅仅是PID参数应设置不同，只要参数设置得当均可以达到很好的效果。均可以达到0.1%，甚至更高的控制要求。

PID控制的不足

　　1. 在实际工业生产过程往往具有非线性、时变不确定，难以建立精确的数学模型，常规的PID控制器不能达到理想的控制效果；

　　2. 在实际生产现场中，由于受到参数整定方法烦杂的困扰，常规PID控制器参数往往整定不良、效果欠佳，对运行工况的适应能力很差。

二、PID控制器各校正环节

   任何闭环控制系统的首要任务是要稳（稳定）、快（快速）、准（准确）的响应命令。PID调整的主要工作就是如何实现这一任务。

　　增大比例系数P将加快系统的响应，它的作用于输出值较快，但不能很好稳定在一个理想的数值，不良的结果是虽较能有效的克服扰动的影响，但有余差出现，过大的比例系数会使系统有比较大的超调，并产生振荡，使稳定性变坏。积分能在比例的基础上消除余差，它能对稳定后有累积误差的系统进行误差修整，减小稳态误差。微分具有超前作用，对于具有容量滞后的控制通道，引入微分参与控制，在微分项设置得当的情况下，对于提高系统的动态性能指标，有着显著效果，它可以使系统超调量减小，稳定性增加，动态误差减小。

   综上所述，P—比例控制系统的响应快速性，快速作用于输出，好比"现在"（现在就起作用，快），I—积分控制系统的准确性，消除过去的累积误差，好比"过去"（清除过去积怨，回到准确轨道），D—微分控制系统的稳定性，具有超前控制作用，好比"未来"（放眼未来，未雨绸缪，稳定才能发展）。当然这个结论也不可一概而论，只是想让初学者更加快速的理解PID的作用。

　　在调整的时候，你所要做的任务就是在系统结构允许的情况下，在这三个参数之间权衡调整，达到最佳控制效果，实现稳快准的控制特点。

   比例控制可快速、及时、按比例调节偏差，提高控制灵敏度，但有静差，控制精度低。积分控制能消除偏差，提高控制精度、改善稳态性能，但易引起震荡，造成超调。微分控制是一种超前控制，能调节系统速度、减小超调量、提高稳定性，但其时间常数过大会引入干扰、系统冲击大，过小则调节周期长、效果不显著。比例、积分、微分控制相互配合，合理选择PID调节器的参数，即比例系数KP、积分时间常数τi和微分时间常数τD，可迅速、准确、平稳的消除偏差，达到良好的控制效果。

　　1. 比例环节

   成比例地反映控制系统的偏差信号e(t)，偏差一旦产生，控制器立即产生控制作用，以减小偏差。当仅有比例控制时系统输出存在稳态误差（Steady-state error）。

   P参数越小比例作用越强，动态响应越快，消除误差的能力越强。但实际系统是有惯性的，控制输出变化后，实际y(t)值变化还需等待一段时间才会缓慢变化。由于实际系统是有惯性的，比例作用不宜太强，比例作用太强会引起系统振荡不稳定。P参数的大小应在以上定量计算的基础上根据系统响应情况，现场调试决定，通常将P参数由大向小调，以能达到最快响应又无超调(或无大的超调)为最佳参数。

　　优点:调整系统的开环比例系数，提高系统的稳态精度，减低系统的惰性，加快响应速度。

　　缺点:仅用P控制器,过大的开环比例系数不仅会使系统的超调量增大，而且会使系统稳定裕度变小，甚至不稳定。
　　
　　2. 积分环节

   控制器的输出与输入误差信号的积分成正比关系。主要用于消除静差，提高系统的无差度。积分作用的强弱取决于积分时间常数T,T越大，积分作用越弱，反之则越强。

　　为什么要引进积分作用？

   比例作用的输出与误差的大小成正比，误差越大，输出越大，误差越小，输出越小，误差为零，输出为零。由于没有误差时输出为零，因此比例调节不可能完全消除误差，不可能使被控的PV值达到给定值。必须存在一个稳定的误差，以维持一个稳定的输出，才能使系统的PV值保持稳定。这就是通常所说的比例作用是有差调节，是有静差的，加强比例作用只能减少静差，不能消除静差(静差：即静态误差，也称稳态误差)。

   为了消除静差必须引入积分作用，积分作用可以消除静差，以使被控的y(t)值最后与给定值一致。引进积分作用的目的也就是为了消除静差，使y(t)值达到给定值，并保持一致。

   积分作用消除静差的原理是，只要有误差存在，就对误差进行积分，使输出继续增大或减小，一直到误差为零，积分停止，输出不再变化，系统的PV值保持稳定，y(t)值等于u(t)值，达到无差调节的效果。

   但由于实际系统是有惯性的，输出变化后，y(t)值不会马上变化，须等待一段时间才缓慢变化，因此积分的快慢必须与实际系统的惯性相匹配，惯性大、积分作用就应该弱，积分时间I就应该大些，反之而然。如果积分作用太强，积分输出变化过快，就会引起积分过头的现象，产生积分超调和振荡。通常I参数也是由大往小调，即积分作用由小往大调，观察系统响应以能达到快速消除误差，达到给定值，又不引起振荡为准。

   对一个自动控制系统，如果在进入稳态后存在稳态误差，则称这个控制系统是有稳态误差的或简称有差系统（System with Steady-state Error）。为了消除稳态误差，在控制器中必须引入“积分项”。积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。因此，比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。PI控制器不但保持了积分控制器消除稳态误差的“记忆功能”，而且克服了单独使用积分控制消除误差时反应不灵敏的缺点。

　　优点：消除稳态误差。
　　
　　缺点：积分控制器的加入会影响系统的稳定性，使系统的稳定裕度减小。

　　3. 微分环节

   反映偏差信号的变化趋势，并能在偏差信号变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。

　　为什么要引进微分作用？

   前面已经分析过，不论比例调节作用，还是积分调节作用都是建立在产生误差后才进行调节以消除误差，都是事后调节，因此这种调节对稳态来说是无差的，对动态来说肯定是有差的，因为对于负载变化或给定值变化所产生的扰动，必须等待产生误差以后，然后再来慢慢调节予以消除。

   但一般的控制系统，不仅对稳定控制有要求，而且对动态指标也有要求，通常都要求负载变化或给定调整等引起扰动后，恢复到稳态的速度要快，因此光有比例和积分调节作用还不能完全满足要求，必须引入微分作用。比例作用和积分作用是事后调节(即发生误差后才进行调节)，而微分作用则是事前预防控制，即一发现y(t)有变大或变小的趋势，马上就输出一个阻止其变化的控制信号，以防止出现过冲或超调等。
D越大，微分作用越强，D越小，微分作用越弱。系统调试时通常把D从小往大调，具体参数由试验决定。

   如：由于给定值调整或负载扰动引起y(t)变化，比例作用和微分作用一定等到y(t)值变化后才进行调节，并且误差小时，产生的比例和积分调节作用也小，纠正误差的能力也小，误差大时，产生的比例和积分作用才增大。因为是事后调节动态指标不会很理想。而微分作用可以在产生误差之前一发现有产生误差的趋势就开始调节，是提前控制，所以及时性更好，可以最大限度地减少动态误差，使整体效果更好。但微分作用只能作为比例和积分控制的一种补充，不能起主导作用，微分作用不能太强，太强也会引起系统不稳定，产生振荡，微分作用只能在P和I调好后再由小往大调，一点一点试着加上去。

   自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。其原因是由于存在有较大惯性组件（环节）或有滞后(delay)组件，具有抑制误差的作用，其变化总是落后于误差的变化。解决的办法是使抑制误差的作用的变化“超前”，即在误差接近零时，抑制误差的作用就应该是零。这就是说，在控制器中仅引入“比例”项往往是不够的，比例项的作用仅是放大误差的幅值，而目前需要增加的是“微分项”，它能预测误差变化的趋势。这样，具有比例+微分的控制器，就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超调。所以对有较大惯性或滞后的被控对象，比例+微分(PD)控制器能改善系统在调节过程中的动态特性。PD控制只在动态过程中才起作用，对恒定稳态情况起阻断作用。因此，微分控制在任何情况下都不能单独使用。

　　优点：使系统的响应速度变快，超调减小，振荡减轻，对动态过程有“预测”作用。

   在低频段，主要是PI控制规律起作用，提高系统型别，消除或减少稳态误差；在中高频段主要是PD规律起作用，增大截止频率和相角裕度，提高响应速度。因此，控制器可以全面地提高系统的控制性能。

三、PID控制器的参数整定

   PID控制器的参数整定是控制系统设计的核心内容。它是根据被控过程的特性确定PID控制器的比例系数、积分时间和微分时间的大小。PID控制器参数整定的方法很多，概括起来有两大类：

　　1. 理论计算整定法

   它主要是依据系统的数学模型，经过理论计算确定控制器参数。这种方法所得到的计算数据未必可以直接用，还必须通过工程实际进行调整和修改。

　　2. 工程整定方法

   它主要依赖工程经验，直接在控制系统的试验中进行，且方法简单、易于掌握，在工程实际中被广泛采用。PID控制器参数的工程整定方法，主要有临界比例法、反应曲线法和衰减法。三种方法各有其特点，其共同点都是通过试验，然后按照工程经验公式对控制器参数进行整定。但无论采用哪一种方法所得到的控制器参数，都需要在实际运行中进行最后调整与完善。现在一般采用的是临界比例法。利用该方法进行 PID控制器参数的整定步骤如下：

　　(1)首先预选择一个足够短的采样周期让系统工作；

　　(2)仅加入比例控制环节，直到系统对输入的阶跃响应出现临界振荡，记下这时的比例放大系数和临界振荡周期；

　　(3)在一定的控制度下通过公式计算得到PID控制器的参数。

　　PID调试一般原则

　　a.在输出不振荡时，增大比例增益P。
　　b.在输出不振荡时，减小积分时间常数Ti。
　　c.在输出不振荡时，增大微分时间常数Td。

　　PID调试一般步骤

　　a. 确定比例增益P

　　确定比例增益P 时，首先去掉PID的积分项和微分项，一般是令Ti=0、Td=0（具体见PID的参数设定说明），使PID为纯比例调节。输入设定为系统允许的最大值的60%~70%，由0逐渐加大比例增益P，直至系统出现振荡；再反过来，从此时的比例增益P逐渐减小，直至系统振荡消失，记录此时的比例增益P，设定PID的比例增益P为当前值的60%~70%。比例增益P调试完成。

　　b. 确定积分时间常数Ti

　　比例增益P确定后，设定一个较大的积分时间常数Ti的初值，然后逐渐减小Ti，直至系统出现振荡，之后在反过来，逐渐加大Ti，直至系统振荡消失。记录此时的Ti，设定PID的积分时间常数Ti为当前值的150%~180%。积分时间常数Ti调试完成。

　　c. 确定微分时间常数Td

　　微分时间常数Td一般不用设定，为0即可。若要设定，与确定 P和Ti的方法相同，取不振荡时的30%。

　　d. 系统空载、带载联调，再对PID参数进行微调，直至满足要求。

   变速积分的基本思想是，设法改变积分项的累加速度，使其与偏差大小相对应：偏差越大，积分越慢；反之则越快，有利于提高系统品质。

 四、麻雀算法

优化问题是科学研究和工程实践领域中的热门问题。智能优化算法大多是受到人类智能、生物群体社会性或自然现象规律的启发，在解空间内进行全局优化。麻雀算法于2020年由薛建凯[1]首次提出，是基于麻雀种群的觅食和反捕食行为的一种新型智能优化算法。

麻雀搜索算法的具体步骤描述以及公式介绍：

构建麻雀种群：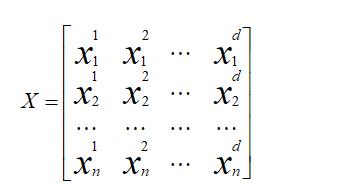

其中，d表示待优化问题的维数，n表示麻雀种群的数量。所有麻雀种群的适应度函数可以表示成如下形式：

其中，Fx表示适应度函数值。

麻雀算法中的麻雀具有两大类分别是发现者和加入者，发现者负责为整个种群寻找食物并为加入者提供觅食的方向，因此，发现者的觅食搜索范围要比加入者的觅食搜索范围大。在每次迭代过程中，发现者按照公式（3）进行迭代。

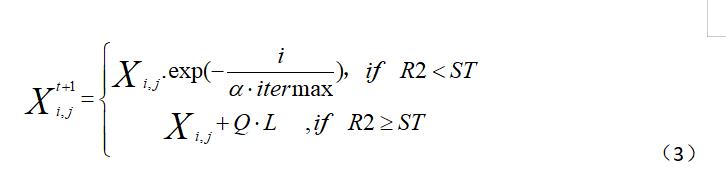
其中，t表示当前迭代次数，Xij表示第i个麻雀种群在第j维中的位置信息,阿尔法表示的0到1的随机数，itermax表示最大迭代次数，Q表示一个服从正态分布的随机数，L是一个1*d并且元素全为1的矩阵，R2属于0-1表示麻雀种群位置的预警值，ST属于0.5-1表示麻雀种群位置的安全值。

当R2<ST时表示 预警值小于安全值，此时觅食环境中没有捕食者，发现者可以进行广泛搜索操作；当R2>ST时意味着种群中有部分麻雀已经发现捕食者，并向种群中的其他麻雀发出预警，所有麻雀都需要飞往安全区域进行觅食。

在觅食过程中，部分加入者会时刻监视发现者，当发现者发现更好的食物，加入者会与其进行争夺，若成功，会立即获得该发现者的食物，否则加入者按照公式（4）进行位置更新。

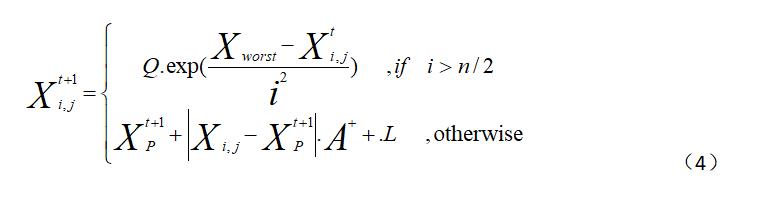
其中，XP表示目前发现者所发现的最优位置，Xworst表示当前全局最差的位置，A表示其元素随机赋值为1或-1的1*d的矩阵并且满足一下关系：

L仍然是一个1*d并且元素全为1的矩阵。当i>n/2时这表明第i个加入者没有获得食物，处于饥饿状态，此时需要飞往其他地方进行觅食，以获得更多的能量。

在麻雀种群中，意识到危险的麻雀数量占总数的10%到20%，这些麻雀的位置是随机产生的，按照公式（5）对意识到危险的麻雀的位置进行不断更新。

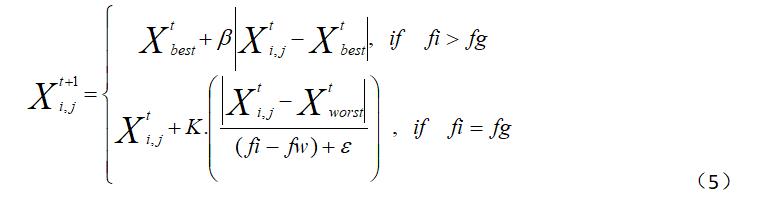
其中，Xbest表示当前全局最优位置，是服从标准正态分布的随机数用来作为步长控制参数，贝塔是一个属于-1到1的随机数，fi表示当前麻雀个体的适应度值，fg表示全局最佳适应度值，fw表示全局最差适应度值，像左耳朵一样的这个是读"一不洗诺"吗？"一不洗诺"表示一个避免分母为0的常数。当fi>fg时表示此时麻雀处于种群边缘，极易受到捕食者的攻击，当fi=fg时表示处于种群中间的麻雀也受到了危险，此时需要靠近其他麻雀以减少被捕食的风险。

五、演示代码

function [FoodFitness,FoodPosition,Convergence_curve]=SSA(N,Max_iter,lb,ub,dim,fobj)
if size(ub,1)==1
    ub=ones(dim,1)*ub;
    lb=ones(dim,1)*lb;
end
Convergence_curve = zeros(1,Max_iter);
%Initialize the positions of salps
SalpPositions=initialization(N,dim,ub,lb);
FoodPosition=zeros(1,dim);
FoodFitness=inf;
%calculate the fitness of initial salps
for i=1:size(SalpPositions,1)
    SalpFitness(1,i)=fobj(SalpPositions(i,:));
end
[sorted_salps_fitness,sorted_indexes]=sort(SalpFitness);
for newindex=1:N
    Sorted_salps(newindex,:)=SalpPositions(sorted_indexes(newindex),:);
end
FoodPosition=Sorted_salps(1,:);
FoodFitness=sorted_salps_fitness(1);
%Main loop
l=2; % start from the second iteration since the first iteration was dedicated to calculating the fitness of salps
while l<Max_iter+1
    c1 = 2*exp(-(4*l/Max_iter)^2); % Eq. (3.2) in the paper
    for i=1:size(SalpPositions,1)
        SalpPositions= SalpPositions';
        if i<=N/2
            for j=1:1:dim
                c2=rand();
                c3=rand();
                %%%%%%%%%%%%% % Eq. (3.1) in the paper %%%%%%%%%%%%%%
                if c3<0.5 
                    SalpPositions(j,i)=FoodPosition(j)+c1*((ub(j)-lb(j))*c2+lb(j));
                else
                    SalpPositions(j,i)=FoodPosition(j)-c1*((ub(j)-lb(j))*c2+lb(j));
                end
                %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
            end
        elseif i>N/2 && i<N+1
            point1=SalpPositions(:,i-1);
            point2=SalpPositions(:,i);
            SalpPositions(:,i)=(point2+point1)/2; % % Eq. (3.4) in the paper
        end
        SalpPositions= SalpPositions';
    end
    for i=1:size(SalpPositions,1)
        Tp=SalpPositions(i,:)>ub';Tm=SalpPositions(i,:)<lb';SalpPositions(i,:)=(SalpPositions(i,:).*(~(Tp+Tm)))+ub'.*Tp+lb'.*Tm;
        SalpFitness(1,i)=fobj(SalpPositions(i,:));
        if SalpFitness(1,i)<FoodFitness
            FoodPosition=SalpPositions(i,:);
            FoodFitness=SalpFitness(1,i); 
        end
    end
    Convergence_curve(l)=FoodFitness;
    l = l + 1;
end

六、仿真结果

 

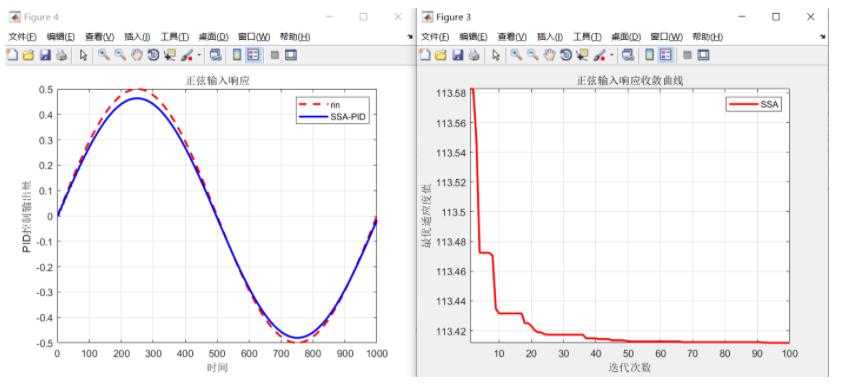
 七、参考文献及代码私信博主

[1]严家政,专祥涛.基于强化学习的参数自整定及优化算法[J/OL].智能系统学报,{3},{4}{5}:1-7[2021-07-14].http://kns.cnki.net/kcms/detail/23.1538.TP.20210622.1109.004.html.