《深入浅出图神经网络》GNN原理解析☄学习笔记图的概述
Posted 白鳯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《深入浅出图神经网络》GNN原理解析☄学习笔记图的概述相关的知识,希望对你有一定的参考价值。
《深入浅出图神经网络》GNN原理解析☄学习笔记(一)图的概述
文章目录
图的基本定义
普遍表示如下,其中V(Vertex)表示顶点集,E(Edge)表示边集。通常用n表示顶点数,m表示边数。
G
=
(
V
,
E
)
G=(V,E)
G=(V,E)
一 条 连 接 顶 点 v i , v j ∈ V 的 边 记 为 ( v i , v j ) 或 者 e i j 一条连接顶点v_i,v_j∈V的边记为(v_i,v_j)或者e_{ij} 一条连接顶点vi,vj∈V的边记为(vi,vj)或者eij
图的基本类型
- 有向图和无向图
- 非加权图与加权图
- 连通图与非连通图
- 二部图,也称为二分图,如作者与论文、演员与电影
邻居和度
v i 的 所 有 邻 居 为 集 合 N ( v i ) , 即 N ( v i ) = { v j ∣ e i j ∈ E , e j i ∈ E } v_i的所有邻居为集合N(v_i),即N(v_i)=\\{v_j|e_{ij}∈E , e_{ji}∈E\\} vi的所有邻居为集合N(vi),即N(vi)={vj∣eij∈E,eji∈E}
以 v i 为 端 点 的 边 的 数 目 称 为 v i 的 度 , 记 为 d e g ( v i ) = ∣ N ( v i ) ∣ 以v_i为端点的边的数目称为v_i的度,记为deg(v_i)=|N(v_i)| 以vi为端点的边的数目称为vi的度,记为deg(vi)=∣N(vi)∣
出度(Outdegree),入度(Indegree)
子图与路径
子图(Subgraph)
路
径
的
长
度
:
L
(
P
i
j
)
=
∣
P
i
j
∣
路径的长度:L(P_{ij})=|P_{ij}|
路径的长度:L(Pij)=∣Pij∣
顶 点 的 距 离 : d ( v i , v j ) = m i n ( ∣ P i j ∣ ) 顶点的距离:d(v_i,v_j)=min(|P_{ij}|) 顶点的距离:d(vi,vj)=min(∣Pij∣)
k 阶 邻 居 : 若 d ( v i , v j ) = k , 我 们 称 v j 为 v i 的 k 阶 邻 居 k阶邻居:若d(v_i,v_j)=k,我们称v_j为v_i的k阶邻居 k阶邻居:若d(vi,vj)=k,我们称vj为vi的k阶邻居
k 阶 子 图 ( k − s u b g r a p h ) : 一 个 顶 点 与 它 的 小 于 等 于 k 阶 的 邻 居 和 边 组 成 的 子 图 k阶子图(k-subgraph):一个顶点与它的小于等于k阶的邻居和边组成的子图 k阶子图(k−subgraph):一个顶点与它的小于等于k阶的邻居和边组成的子图
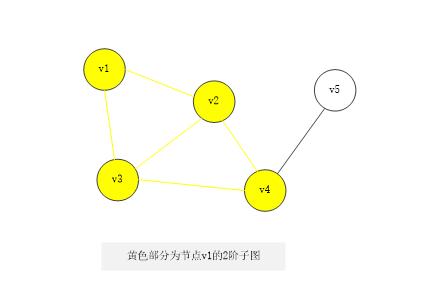
图的存储与遍历
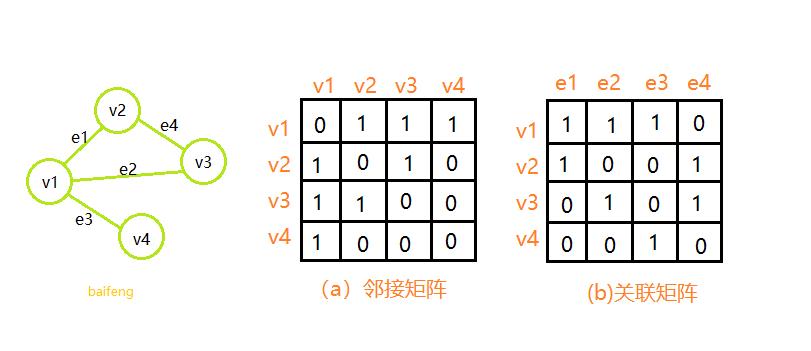
邻接矩阵和关联矩阵
邻接矩阵(Adjacency matrix):一个一维数组表示顶点集合,一个二维数组(v,v)表示邻接矩阵。
关联矩阵(Incidence matrix):两个一维数组分别表示顶点集合和边集合,一个二维数组(v, e)表示关联矩阵。
图的遍历
深度优先搜索(DFS,Depth-First-Search)
广度优先搜索(BFS,Breadth-First-Search)
详细算法见往期博客图论(graph)相关算法总结,内有详细示例和代码,此处不赘述。
图数据的应用场景
在实际的数据场景中,通常将图称为网络(Network),顶点和边分别称为节点(Node)和关系(Link)。
图数据类别
- 同构图(Homogeneous Graph):图中的节点类型和关系类型都仅有一种,如万维网
- 异构图(Heterogeneous Graph):图中的节点类型和关系类型多于一种
- 属性图(Property Graph):相较于异构图,属性图中节点和关系都有标签(Label)和属性(Property)
- 非显式图(Graph Constructed from Non-relational Data):数据之间没有显式地定义出关系,需要依据某种规则或计算方式将数据的关系表达出来,进而将数据当成一种图数据进行研究。
图数据的应用场景
- 社交网络:用户重要性排名和用户推荐
- 电子购物:用户与商品(二部图),推荐系统
- 化学分子:分子与化学键,研究新材料和新药物
- 交通网络:路径规划、流量规划
- 场景图:图像合成、图像语义检索、视觉推理等
- 电路设计图:仿真实验
图数据任务分类
-
节点层面(Node Level)
分类任务和回归任务。如学术上论文节点的分类,工业界在线社交网络中用户标签的分类、恶意账户检测等。
-
边层面(Link Level)
边的分类和预测任务。边的分类是指对边的某种性质进行预测;边预测是指给定的两个节点之间是否会构成边。常用在推荐业务中。
-
图层面(Graph Level)
从图的整体出发,实现分类、表示和生成等任务。如对药物分子的分类,酶的分类等。
参考资料:《深入浅出图神经网络》GNN原理解析
以上是关于《深入浅出图神经网络》GNN原理解析☄学习笔记图的概述的主要内容,如果未能解决你的问题,请参考以下文章