压缩感知合集7压缩感知RIP有限等距性：定义解析，理解说明，数学原理推导

Posted 2021-08-13 呆呆象呆呆

0 前情提要

0.1 数学模型和总体框图如下

给定输入信号$\mathbf{X}\in {\mathbb{R}}^{N\times 1}$，最终想要得到压缩信号$\mathbf{A}\in {\mathbb{R}}^{M\times 1}$，$K<<N$

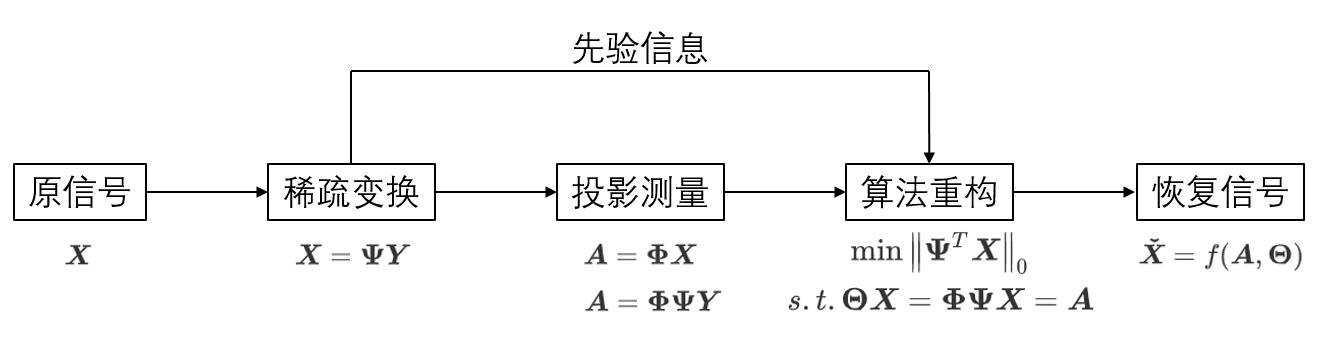
0.2 压缩过程图例分析如下

整个压缩过程也可以被称为感知过程
$$\mathbf{A}=\mathbf{\Phi }\mathbf{X}=\mathbf{\Phi }\mathbf{\Psi }\mathbf{Y}=\mathbf{\Theta }\mathbf{Y}$$

$\mathbf{\Theta }$即为感知过程的核心命名为感知矩阵

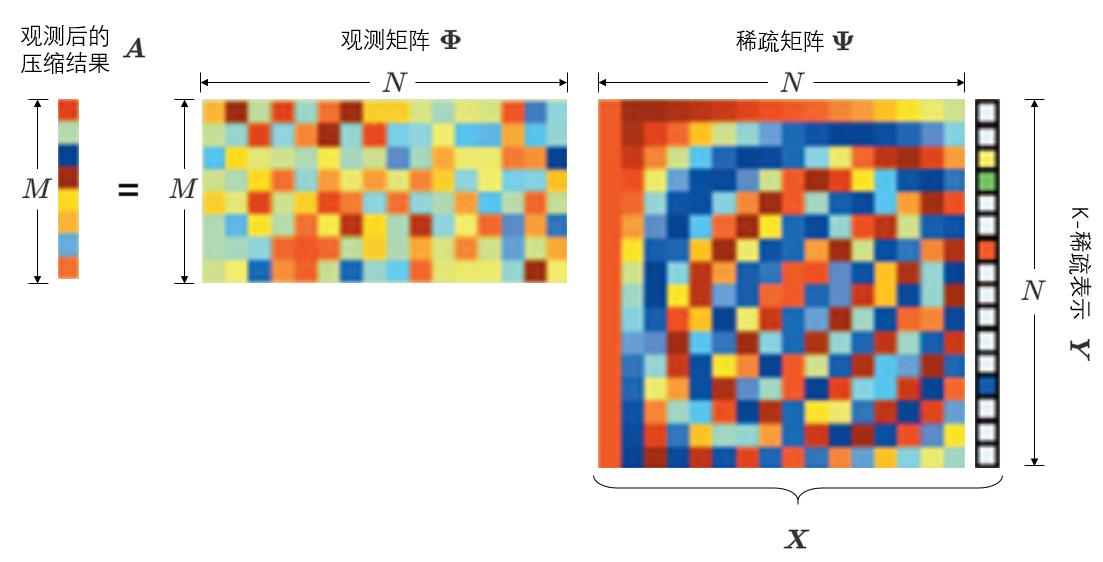
符号	含义	维度	属性
$\mathbf{X}$	输入信号；待压缩信号	${\mathbb{R}}^{N\times 1}$	未知，需要恢复
$\mathbf{\Phi }$	观测矩阵；测量矩阵	${\mathbb{R}}^{M\times N}$	已知（非自适应性）
$\mathbf{\Psi }$	变换矩阵；变换基矩阵；稀疏基矩阵；稀疏矩阵；正交基字典矩阵	${\mathbb{R}}^{N\times N}$	已知（非自适应性）
$\mathbf{Y}$	正交基变换后的稀疏表示	${\mathbb{R}}^{N\times 1}$	未知，需要恢复
$\mathbf{\Theta }$	感知矩阵，传感矩阵	${\mathbb{R}}^{M\times N}$	已知（非自适应性）
$\mathbf{A}$	观测压缩所得到压缩信号	${\mathbb{R}}^{M\times 1}$	已知

0.3 算法重构恢复过程如下

在得到已经压缩完的采样信号$\mathbf{A}$后，根据确定的固定性观测矩阵$\mathbf{\Phi }$和稀疏矩阵$\mathbf{\Psi }$的先验信息进行恢复，数学表达如下
$$\check{\mathbf{X}}=f(\mathbf{A},\mathbf{\Theta })$$
而$M<<N$，欠定方程，一般可以抽象为如下求解任务

$$\begin{gathered} \min {\Vert {\mathbf{\Psi }}^T\mathbf{X}\Vert }_0 \\ s.t.\mathbf{\Theta }\mathbf{X}=\mathbf{\Phi }\mathbf{\Psi }\mathbf{X}=\mathbf{A} \end{gathered}$$

注意

若$N=M$，则可轻松由$\mathbf{A}$解出$\mathbf{X}$和$\mathbf{Y}$

而$M<<N$，可根据稀疏表示下的信号$\mathbf{Y}$和矩阵所具有的RIP性质重构

1 发展历史

RIP是压缩感知领域的一个重要概念，主要可以被用来分析还原算法的表现好坏。

年份	事件	相关论文/Reference
2005	Emmanuel Candès、陶哲轩提出了当\\delta_{2s}<1时可以保证(P0)有唯一解，并且用反证法对此问题进行了证明，大概思路是假设有两个解，会发现从RIP性质的不等式中可以得出这两个解是相等的。	Candes, E.; Tao, T. (2005). Decoding by linear programming. IEEE Transactions on Information Theory. 59(8):4203-4215.
2006	Emmanuel Candès、陶哲轩和David Donoho证明了在已知信号稀疏性的情况下，可能凭借较采样定理所规定更少的采样数重建原信号，这一理论也是压缩感知的基石。	Candès, E.; Romberg, J. K.; Tao, T. (2006). Stable signal recovery from incomplete and inaccurate measurements. Communications on Pure and Applied Mathematics. 59 (8): 1207–1223.
2007	Richard Baraniuk等人提出了一种简单的技术，用于验证压缩感知基础的随机矩阵的RIP性质。	Baraniuk, R.G., Davenport, M.A., DeVore, R.A., & Wakin, M.B. (2007). A Simple Proof of the Restricted Isometry Property for Random Matrices.
2008	Emmanuel Candès证明了当 ${\delta }_{2K}<1$ 时可以保证零范数问题有唯一的稀疏解，而当 ${\delta }_{2s}s<\sqrt{2}-1$ 时则可以保证0范数和1范数等价。零范数求解为NP-hard问题，在此前提下将其转化为1范数求最优化问题，这时是个凸优化，对于求解很有帮助。	Candes, E. (2008). The restricted isometry property and its implications for compressedsensing. Comptes Rendus Mathematique. 346(8-9): 589-592.

2 本篇的主要思路

前文有一定的简单介绍和逻辑分析（【压缩感知合集6】压缩感知为什么可以恢复信号；为什么需要满足稀疏性条件、RIP条件、矩阵不相关等限制条件才可以恢复信号的逻辑分析）这一篇文章我们详细理解一下，这个条件的必要性

主要的问题如下

• RIP性质是什么？
• 为什么需要RIP性质？
• 为什么介绍K阶RIP性质后恢复K稀疏信号又要用2K阶RIP性质？

3 RIP性质定义

RIP性质：有限等距性质（Restricted Isometry Property，RIP）

不同文献上表达RIP的方式不同，一般主要有以下几种（为了不影响理解我将论文中使用的一些字母进行了替换，换成了我前文例子中的字母表示，但是不影响他对性质的具体定义）：

中文定义一

传感矩阵 $\mathbf{\Theta }$ 的RIP参数 ${\delta }_k$ 为满足下式的最小值 $\delta$
$$(1-\delta )\Vert \mathbf{Y}{\Vert }_2^2⩽{\Vert \mathbf{\Theta }\mathbf{Y}\Vert }_2^2⩽(1+\delta )\Vert \mathbf{Y}{\Vert }_2^2$$
其中 $\mathbf{Y}$ 为 $K$ 稀疏信号。若 ${\delta }_K<1$ ，则称测量矩阵 $\mathbf{\Theta }$ 满足 $K$ 阶RIP。

王强，李佳，沈毅.压缩感知中确定性测量矩阵构造算法综述[J]. 电子学报，2013，41(10)：2041-2050.

中文定义二

为了重构稀疏信号，Candès和Tao给出并证明了传感矩阵 $\mathbf{\Theta }$ 必须满足约束等距性条件。

对于任意 $\mathbf{c}\in {\mathbf{R}}^{|T|}$ 和存在常数 ${\delta }_K\in (0,1)$ , 如果
$$\left(1-{\delta }_K\right)\Vert \mathbf{c}{\Vert }_2^2\le {\Vert {\mathbf{\Theta }}_T\mathbf{c}\Vert }_2^2\le \left(1+{\delta }_K\right)\Vert \mathbf{c}{\Vert }_2^2$$
成立，其中 T ⊂ { 1 , ⋯   , N } T \\subset\\{1, \\cdots, N\\} T⊂{1,⋯,N} ，

以上是关于压缩感知合集7压缩感知RIP有限等距性：定义解析，理解说明，数学原理推导的主要内容，如果未能解决你的问题，请参考以下文章

压缩感知合集6压缩感知为什么可以恢复信号；为什么需要满足稀疏性条件RIP条件矩阵不相关等限制条件才可以恢复信号的逻辑分析

压缩感知合集3压缩感知的背景与意义

压缩感知合集5压缩感知简介和数学模型分析

压缩感知合集2（背景知识）信号稀疏表示的数学推导和解释理解

压缩感知合集1（背景知识）香农奈奎斯特采样定理的数学推导和图解分析

压缩感知合集4理想采样信号和随机采样信号两种采样信号的频谱分析，以及采样效果比较