jzoj3555树的直径

Posted 2021-08-13 SSL_ZZL

树的直径

• 题面
• • Description
  • Input
  • Output
  • Sample Input
  • Sample Output
  • Data Constraint
• 解题思路
• Code

题面

Description

科学家在观测一棵大树，这棵树在不断地生长，科学家给这棵树的每个节点编了号。开始的时候，这棵树很小只有4个节点，一号点为根，其他三个节点挂在上面。
在接下来的M次观察中，科学家每次都能看见这棵树从叶子处长出新的两个节点来。如果当前这棵树有N个节点，那么这棵树的新的两个节点的编号分别为N+1，N+2。科学家记录下了这棵树生长的过程，需要你帮着计算这棵树实时的直径。树的直径就是这棵树最远的两个节点的距离。

Input

第一行一个整数M，代表观察的次数。
接下来M行，每行一个整数x，代表这棵树的编号为x的节点下面又长了两个叶子节点。保证每次生长的节点都是叶子节点。

Output

M行，每次生长后这棵树的直径。

Sample Input

5
2
3
4
8
5

Sample Output

3
4
4
5
6

Data Constraint

对于10%的数据，N<=10
对于40%的数据，N<=1000
对于100%的数据，N<=100000。

---

解题思路

就是很J的一个东西

dep[i]记录以i为根的子树，i节点与最深节点的距离
那么对于以i为根的子树来说，直径 = 左子树最深距离 + 右子树最深 + 2
这个直径并不需要记录，每次可以直接套公式算出来
ans = max(ans, dep[son[i][1]] + dep[son[i][2]] + 2)

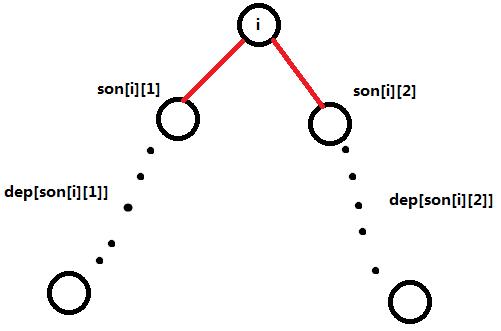
更新dep[]和ans
每次dep[]的更新只跟 当前新加的点 到 根节点 之间的dep[]有关

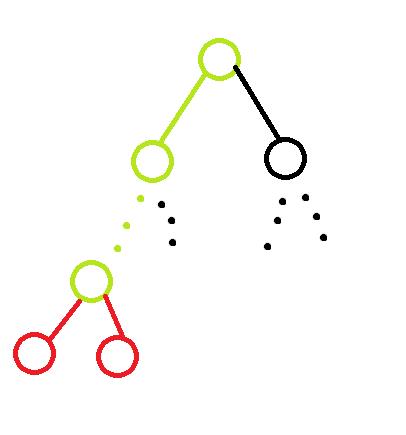
所以更新dep[]时就从新节点往父节点爬，ans也同时更新

当dep[]已经无法更新时，就可以直接退出了

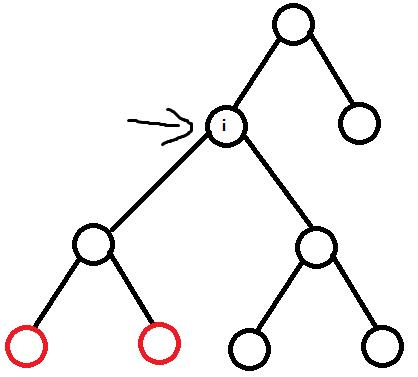
这时dep[i]为2，无法再变大，dep不变大，ans也不会变大，那么就可以退出了
注意：要先更新ans，再判断退不退出
比如上面的图，左边的dep[son[i][1]]原本1，现在是2
现在 以i为根节点的子树 直径为4，可能更新ans，但dep[i]还是2，不会影响到上面的dep和ans

---

Code

#include <iostream>
#include <cstdio>

using namespace std;

int n, m, x, fa[500100], son[500100][3], ans, dep[500100];

void init() {
	dep[1] = 1; 
	fa[2] = fa[3] = fa[4] = 1;
	ans = 2;
	n = 4;
}

void change(int x) {  //加入新节点
	fa[n + 1] = fa[n + 2] = x;
	son[x][1] = n + 1, son[x][2] = n + 2;
	n += 2;
}

void work(int x) {
	while(fa[x] != 1) {
		int k = son[fa[x]][1];
		if(x == son[fa[x]][1]) k = son[fa[x]][2];  //找兄弟
		ans = max(ans, dep[x] + dep[k] + 2);
		
		if(dep[fa[x]] >= dep[x] + 1)  //无法更新dep
			break;
		dep[fa[x]] = dep[x] + 1;
		x = fa[x];
	}
	if(x == 2){  //因为比较懒， 所以写的很丑，可以专门写个函数用来查找x的兄弟
		int k = max(dep[3], dep[4]);
		ans = max(ans, dep[x] + k + 2);
		dep[fa[x]] = max(dep[fa[x]], dep[x] + 1);
	} else if(x == 3){
		int k = max(dep[2], dep[4]);
		ans = max(ans, dep[x] + k + 2);
		dep[fa[x]] = max(dep[fa[x]], dep[x] + 1);
	} else if(x == 4){
		int k = max(dep[2], dep[3]);
		ans = max(ans, dep[x] + k + 2);
		dep[fa[x]] = max(dep[fa[x]], dep[x] + 1);
	}
}

int main() {
	init(); 
	scanf("%d", &m);
	for(int i = 1; i <= m; i++) {
		scanf("%d", &x);
		change(x);
		work(n);
		printf("%d\\n", ans);
	}
}