第六周.01.GIN带读

Posted 2021-08-13 oldmao_2001

文章目录

• 摘要
• Introduction
• PRELIMINARIES
• 几种聚合函数的使用场景讨论

本文内容整理自深度之眼《GNN核心能力培养计划》
公式输入请参考： 在线Latex公式

本次学习：
How Powerful are Graph Neural Networks

摘要

GNN很重要
Graph Neural Networks (GNNs) are an effective framework for representation learning of graphs.

GNN的原理是
GNNs follow a neighborhood aggregation scheme, where the representation vector of a node is computed by recursively aggregating and transforming representation vectors of its neighboring nodes.

GNN变体（GCN、GraphSage）取得的效果很SOTA
Many GNN variants have been proposed and have achieved state-of-the-art results on both node and graph classification tasks.

转折，缺乏理论探索
However, despite GNNs revolutionizing graph representation learning, there is limited understanding of their representational properties and limitations.

我们咋做
Here, we present a theoretical framework for analyzing the expressive power of GNNs to capture different graph structures.

结果咋样
Our results characterize the discriminative power of popular GNN variants, such as Graph Convolutional Networks and GraphSAGE, and show that they cannot learn to distinguish certain simple graph structures.

我们还做了啥
We then develop a simple architecture that is provably the most expressive among the class of GNNs and is as powerful as the Weisfeiler-Lehman graph isomorphism test.

效果杠杠的。
We empirically validate our theoretical findings on a number of graph classification benchmarks, and demonstrate that our model achieves state-of-the-art performance.

Introduction

背景忽略
里面讲了一段本文结论总结：
1)We show that GNNs are at most as powerful as the WL test in distinguishing graph structures.
GNN的表达上限是WL test
2) We establish conditions on the neighbor aggregation and graph readout functions under which the resulting GNN is as powerful as the WL test.
当GNN到达WL test上限的情况下，确定了邻居汇聚方法以及全图表征函数
3) We identify graph structures that cannot be distinguished by popular GNN variants, such as GCN (Kipf & Welling, 2017) and GraphSAGE (Hamilton et al., 2017a), and we precisely characterize the kinds of graph structures such GNN-based models can capture.
给出了GCN和GraphSAGE无法正确捕获节点表征的例子（5.2最后一段）

4. We develop a simple neural architecture, Graph Isomorphism Network (GIN), and show that its discriminative/representational power is equal to the power of the WL test.
   本文给出的GIN模型，可达到WL test的效果

PRELIMINARIES

GNN中最关键的两个步骤是AGGREGATE和COMBINE
其中GCN的AGGREGATE选择的是MEAN POOLING
GraphSAGE的AGGREGATE选择的是MAX POOLING
关于图的同构判断问题可以参考：深度之眼Paper带读笔记GNN.07.GraphSAGE
这里要补充的是如果两个图经过WL test的迭代得到不同结果，代表两个图不同构；如果两个图经过WL test的迭代得到相同结果，并不能代表两个图一定同构。
The WL test iteratively
(1) aggregates the labels of nodes and their neighborhoods,
这个步骤和GNN的消息汇聚是一样的；
(2) hashes the aggregated labels into unique new labels.
这个步骤里面的hash函数是关键，这里的hash函数应该可以替换为其他单射函数（下面那个例子用的是SUM）。
这里老师给了另外一个例子：
https://davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/
这里要补充一下，这个例子里面在收集邻居信息的时候，为了不丢失邻居信息，用的是multiset，不是set，multiset里面是可以有重复元素的。
原文的定义如下：
Definition 1 (Multiset). A multiset is a generalized concept of a set that allows multiple instances for its elements. More formally, a multiset is a 2-tuple $X=(S;m)$ where $S$ is the underlying set of $X$ that is formed from its distinct elements, and $m$ : $S\to N\ge 1$ gives the multiplicity of the elements.
写这个是因为后面的推导要用到，给个例子，有一个multiset，里面有5个元素， { 4 , 4 , 4 , 3 , 3 } \\{4,4,4,3,3\\} {4,4,4,3,3}，那么按照上面的定义就可以写为： X = { ( 4 ; 3 ) , ( 3 ; 2 ) } , S = { 4 , 3 } X=\\{(4;3),(3;2)\\},S=\\{4,3\\} X={(4;3),(3;2)},S={4,3}，简单的说：$S$是$X$的子集，$m$表示$S$中元素的重复次数。

原文提到，一个牛叉的GNN应该可以区分不同结构的邻居汇聚过来的信息，WL Test做的就是这个事，保证这个事情就是因为使用了单射函数。
所以下面原文第四节的标题就是，如果构建powerful的图网：要用单射来进行aggregate和拼接。因此就引出本文提出的模型GIN（4.1节）：使用单射的SUM pooling来做邻居消息的汇聚，然后加上自身的消息后，用的是多层的MLP来处理COMBINE步骤。这里要理解，例如一个2层的GIN，然后每层GIN可以用7层的MLP来处理COMBINE

接下来文章开始分析图表征任务READOUT函数（4.2节）。
主要看公式4.2，这里用到的是每一层GIN获得的节点表征，然后做READOUT，然后做拼接。

几种聚合函数的使用场景讨论

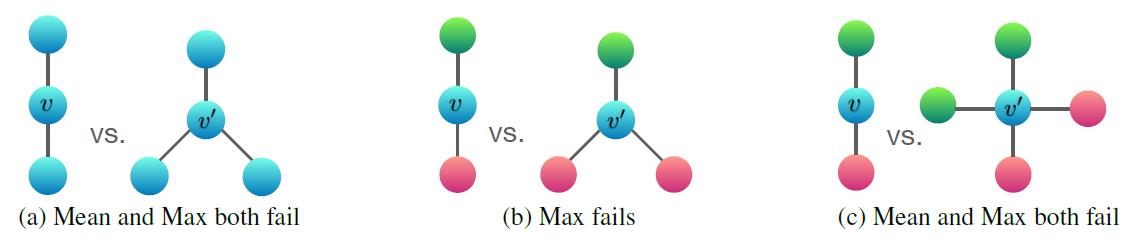
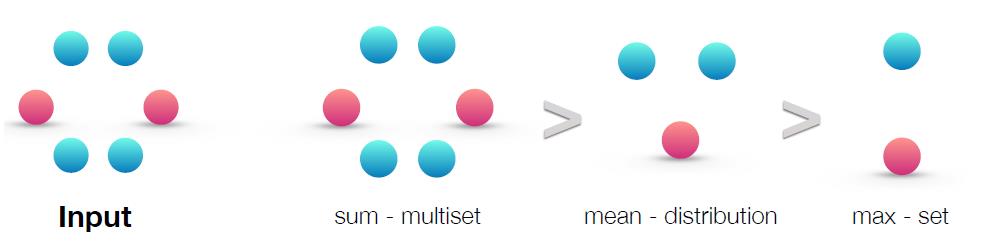
这块是本文的一个亮点，就是原文的图2，给出的结论是：
理论上SUM的表达能力最强，MAX最挫（丢失的信息最多）。（但是实操上打脸这个结论，下面有分析为什么）
当我们不关心所有节点分类的个数，只关心节点类型的分布/比例（proportion/distribution）信息，这个时候用mean pooling最好，可以看到下面的例子经过mean pooling操作后蓝色和红色类别的比例/分布不变（下面有数学表达：$X_1=(S;m),X_2=(S;km)$的情况下，类别一样，类别对应的节点数量是倍数关系，这个时候用mean pooling效果最好）；
当我们只关心哪个邻居节点对当前节点影响最大的时候，用max pooling最合适。

问题：
传统的GCN、GraphSage与本文GIN有什么不同？
1.前者用的是MAX、MEAN pooling，后者用的单射函数来做消息汇聚；
2.前者用的是类似单层MLP的操作，后者用的多层的MLP。单层MLP经证明不满足单射函数条件，多层的拟合能力更加强，可以满足单射函数条件。