二分训练7.14
Posted karshey
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二分训练7.14相关的知识,希望对你有一定的参考价值。
懵逼场。
A - 4 Values whose Sum is 0
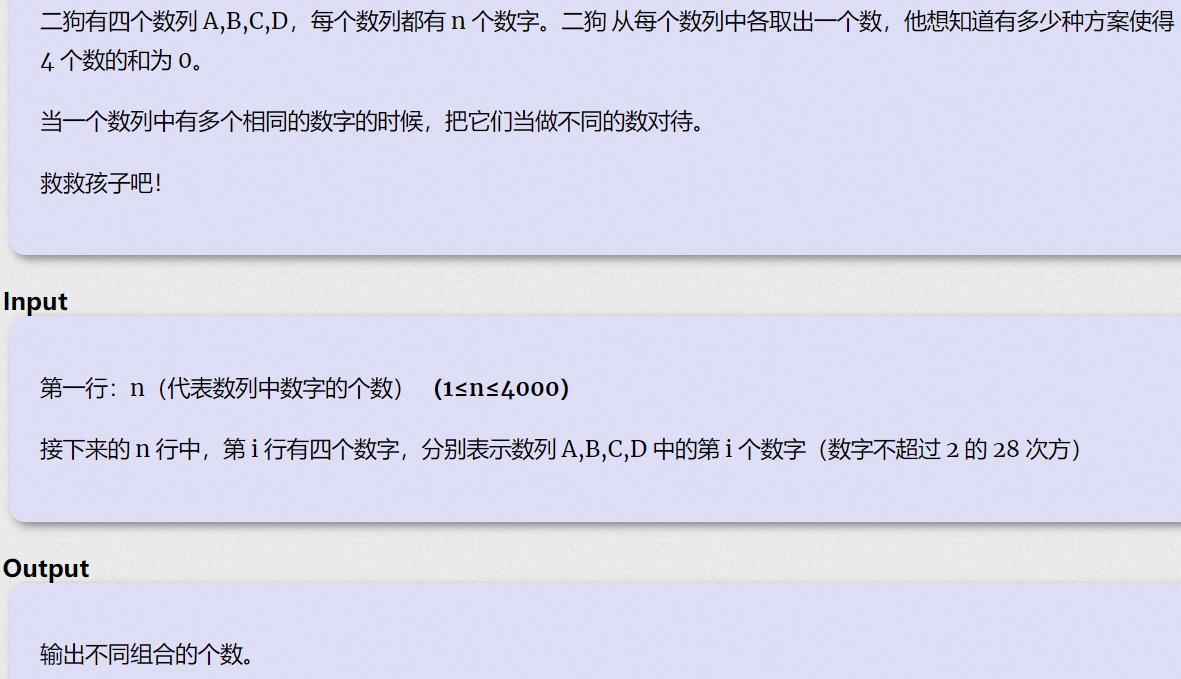
输入:
6
-45 22 42 -16
-41 -27 56 30
-36 53 -37 77
-36 30 -75 -46
26 -38 -10 62
-32 -54 -6 45
输出:
5
Hint:
样例解释: (-45, -27, 42, 30), (26, 30, -10, -46), (-32, 22, 56, -46),(-32, 30, -75, 77), (-32, -54, 56, 30).
按列来看有四组数据,求每组数据各出一个数字之和为0的个数。直接暴力会T,用二分就可以把题目简化为O(n^2)的了。
lower_bound 和upper_bound 的使用:
upper_bound(f,f+temp2,-1*temp)-lower_bound(f,f+temp2,-1*temp); //可以得到在f中值为-1*temp的个数,为0就是没有
代码:
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=4005;
int a[N],b[N],c[N],d[N],e[N*N],f[N*N];
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>a[i]>>b[i]>>c[i]>>d[i];
int temp1=0,temp2=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
e[temp1++]=a[i]+b[j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
f[temp2++]=c[i]+d[j];
}
}
sort(e,e+temp1);
sort(f,f+temp2);
int sum=0;
for(int i=0;i<temp1;i++)
{
int temp=e[i];
sum+=upper_bound(f,f+temp2,-1*temp)-lower_bound(f,f+temp2,-1*temp);
}
cout<<sum;
return 0;
}
B - Pie

输入:
3
3 3
4 3 3
1 24
5
10 5
1 4 2 3 4 5 6 5 4 2
输出:
25.1327
3.1416
50.2655
Hint:
定义pi的方法 const double pi=acos(-1.0);//头文件math.h
三角函数arccos
分饼,大饼可分为小饼,但小饼不能凑成大饼。
二分,上界为所有体积平分,下界为最大值的平分。
参考:https://blog.csdn.net/Love_Jacques/article/details/104140243
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long ll;
const int N=1e4+5;
const double pi=acos(-1.0);
double a[N],sum,maxn=-1;
int n,f;
int judge(double mid)
{
int sum=0;
for(int i=0;i<n;i++)
{
sum+=(int)(a[i]/mid);//一共能分出的蛋糕块数
}
if(sum>=f) return 1;
else return 0;
}
double binary_search()
{
double high=sum/f,low=maxn/f,mid=(high+low)/2;//mid是每人的蛋糕大小
while(high-low>1e-7)
{
if(judge(mid)) low=mid;
else high=mid;
mid=(high+low)/2;
}
return mid;
}
int main()
{
int t;cin>>t;
while(t--)
{
cin>>n>>f;f++;
memset(a,0,sizeof(a));
for(int i=0;i<n;i++)
{
int temp;cin>>temp;
a[i]=pi*temp*temp;
sum+=a[i];
if(a[i]<maxn) maxn=a[i];
}
double ans=binary_search();
printf("%.4f\\n",ans);
}
}
C - Can you find it?

输入:
3 3 3
1 2 3
1 2 3
1 2 3
3
1
4
10
输出:
Case 1:
NO
YES
NO
其实是找是否有a[i]+b[j]==k[k1]-c[z];
要用二分。
二分的while条件是小于等于!!整数有加一减一之分。
#include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long ll;
const int N=505;
int a[N],b[N],c[N],d[N*N],k[1005];
int main()
{
int Case=1,l,n,m;
while(cin>>l>>n>>m)
{
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
memset(d,0,sizeof(d));
memset(k,0,sizeof(k));
for(int i=0;i<l;i++) cin>>a[i];
for(int i=0;i<n;i++) cin>>b[i];
for(int i=0;i<m;i++) cin>>c[i];
int k1;cin>>k1;
for(int i=0;i<k1;i++) cin>>k[i];
printf("Case %d:\\n",Case++);
int tempd=0;
for(int i=0;i<l;i++)
{
for(int j=0;j<n;j++)
{
d[tempd++]=a[i]+b[j];
}
}
sort(d,tempd+d);sort(c,c+m);
for(int i=0;i<k1;i++)
{
int flag=0;
for(int j=0;j<m;j++)
{
int low=0,high=tempd-1,mid=(low+high)/2;
int temp=k[i]-c[j];
if(temp<d[0]) break;//k太小
if(temp>d[high]) continue;//换下一个大点的c
while(low<=high)
{
if(d[mid]==temp){flag++;break;
}
if(d[mid]<temp) low=mid+1;
else high=mid-1;
mid=(high+low)/2;
}
if(flag) break;
}
if(flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
}
return 0;
}
D - A Cubic number and A Cubic Number

输入:
5
7
13
23
2269
5557
输出:
YES
NO
NO
YES
NO
平方差公式:
由于是素数,则只能分成1和它自己。因此,素数本身等于x2+y2+xy;
x^3-y^3=(x-y)*(x^2+y^2+xy);
数据范围是1e12,因此一定要二分和long long;
二分后范围为1e6;
#include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
ll a[N];
int main()
{
//打表
ll temp=0;
for(ll i=1;i<=1e6;i++)
{
a[temp++]=i*i+i*(i+1)+(i+1)*(i+1);
}
sort(a,a+temp);
int t;cin>>t;
while(t--)
{
ll n;cin>>n;
int flag=0;
for(ll i=0;i<temp;i++)
{
if(a[i]==n) {flag=1;break;
}
if(a[i]>n){break;
}
}
if(flag) cout<<"YES";
else cout<<"NO";
cout<<endl;
}
return 0;
}
E - Funky Numbers
原题:https://codeforces.com/problemset/problem/192/A
想要求是否存在a[i]+a[j]==n,就求在范围内是否存在n-a[i];
#include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
ll a[N];
int main()
{
for(ll i=1;i<=N;i++) a[i-1]=i*(i+1)/2;
sort(a,a+N);
ll n;cin>>n;
int flag=0;
for(ll i=0;i<N;i++)
{
ll t=lower_bound(a,a+N,n-a[i])-a;
if(a[i]+a[t]==n)
{
flag=1;break;
}
}
if(flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
return 0;
}
F - Burning Midnight Oil
原题:https://codeforces.com/problemset/problem/165/B
要求最小的v,因此是high减小。
#include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long ll;
const int N=105;
int n,k;
int check(int nn)
{
int sum=nn;
while(nn)
{
sum+=nn/k;
nn/=k;
}
if(sum>=n) return 1;
else return 0;
}
int main()
{
cin>>n>>k;
int low=1,high=n,mid=(low+high)/2;
//求最小的v 因此是high减小
while(low<high)
{
if(check(mid)) high=mid;
else low=mid+1;
mid=(low+high)/2;
}
cout<<mid;
return 0;
}
G - Can you solve this equation?
来源:http://acm.hdu.edu.cn/showproblem.php?pid=2199
高中数学题。先求导得知单调性,可知单调递增。
若x0时大于0,或x100时小于0,那都是无零点的。
开始输出的时候发现输出的总是整数,后来发现习惯性的定义函数形参是int型…
#include<bits/stdc++.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long ll;
const double eps=1e-6;
double y;
double check(double x)
{
double temp=8*x*x*x*x+7*x*x*x+2