杨辉三角_LeetCode

Posted 2021-08-12 勇敢牛牛不怕困难@帅

力扣第118题杨辉三角

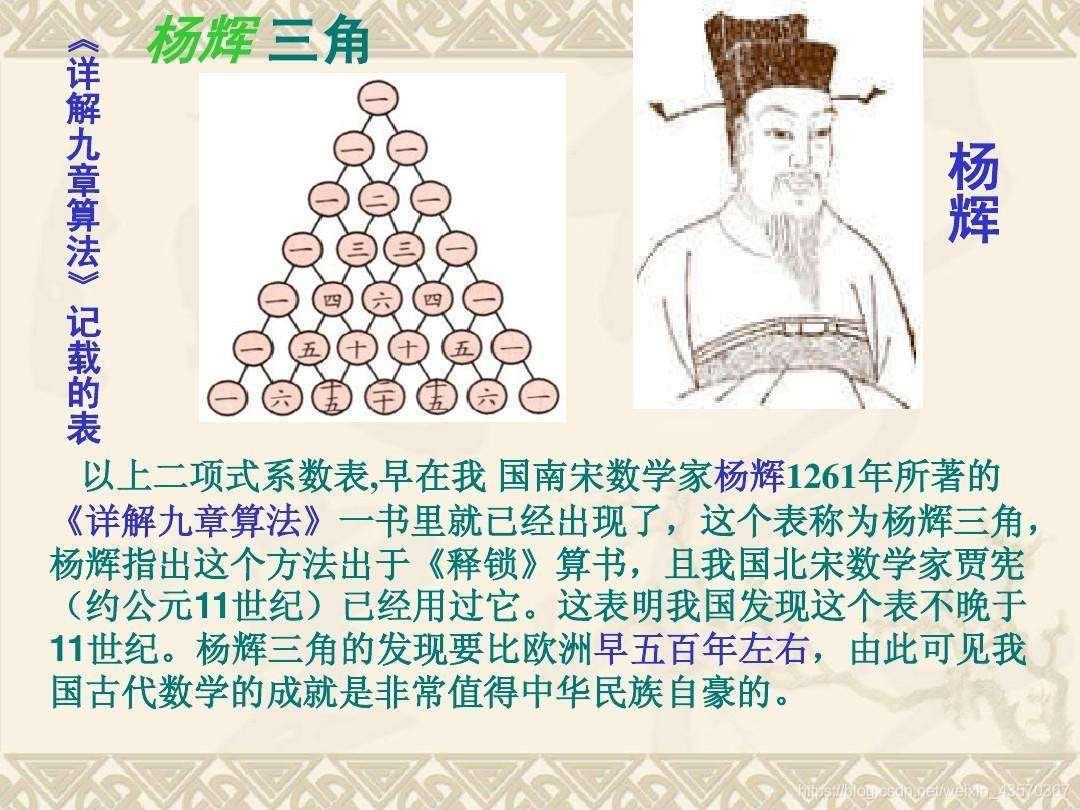
杨辉三角的概念

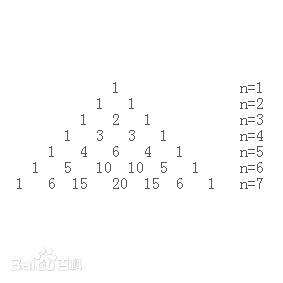
每个数等于它上方两数之和。
每行数字左右对称，由1开始逐渐变大。
第n行的数字有n项。
前n行共[(1+n)n]/2 个数。
第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
第n行的第m个数和第n-m+1个数相等 ，为组合数性质之一。
每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
(a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
将第2n+1行第1个数，跟第2n+2行第3个数、第2n+3行第5个数……连成一线，这些数的和是第4n+1个斐波那契数；将第2n行第2个数(n>1)，跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。
将第n行的数字分别乘以10^{（m-1），其中m为该数所在的列，再将各项相加的和为11}（n-1）。11^0=1，111=1x10^0+1×101=11，11^2=1×100+2x10^1+1x102=121，11^3=1x100+3×10^1+3x102+1x10^3=1331，114=1x10^0+4x101+6x10^2+4x103+1x10^4=14641，115=1x10^0+5x101+10x10^2+10x103+5x10^4+1×105=161051。
第n行数字的和为2^{（n-1）。1=2}（1-1），1+1=2^{（2-1），1+2+1=2}（3-1），1+3+3+1=2^{（4-1），1+4+6+4+1=2}（5-1），1+5+10+10+5+1=2^（6-1）。
斜线上数字的和等于其向左（从左上方到右下方的斜线）或向右拐弯（从右上方到左下方的斜线），拐角上的数字。1+1=2，1+1+1=3，1+1+1+1=4，1+2=3，1+2+3=6，1+2+3+4=10，1+3=4，1+3+6=10，1+4=5。
将各行数字左对齐，其右上到左下对角线数字的和等于斐波那契数列的数字。1，1，1+1=2，2+1=3，1+3+1=5，3+4+1=8，1+6+5+1=13，4+10+6+1=21，1+10+15+7+1=34，5+20+21+8+1=55。

力扣题目如下：

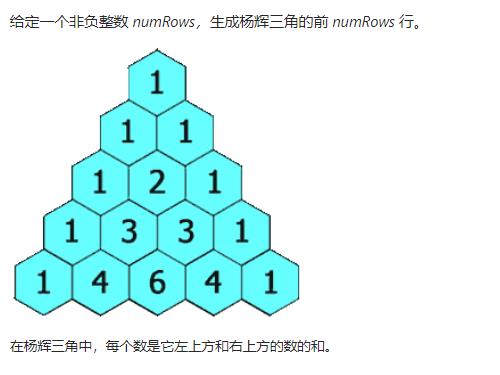
思路：
第一种思路：
在明白什么是杨辉三角的前提下，可以简单的理解为在一个二维的数组中进行操作，边界的值都为1，而中间的值等于上一层前两元素求和而得。

package leetcode;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;

public class Solution {

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		List<ArrayList<Integer>> list = new ArrayList<ArrayList<Integer>>();
		Scanner sc = new Scanner(System.in);
		System.out.println("输入整形数字");
		int number = sc.nextInt();
		int [][]arr = new int[number][number];
		for(int i=0;i<number;i++) {
			for(int j=0;j<=i;j++) {
				if(j==0||j==i) {//边界条件
					arr[i][j]=1;
				}else {
					arr[i][j]=arr[i-1][j-1]+arr[i-1][j];//上一层的j-1和j值的和等于该坐标的值
				}
			}
		}
		for(int i=0;i<number;i++) {
			for(int j=0;j<number;j++) {
				if(arr[i][j]!=0)
				System.out.print(arr[i][j]+ "\\t");
			}
			System.out.println();
		}
		

	}

}

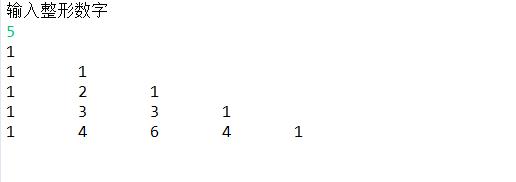
第二种思路：

杨辉三角，是二项式系数在三角形中的一种几何排列。它是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

杨辉三角具有以下性质：

所以我们可以根据性质4，一行一行的计算出杨辉三角。每当我们计算出第 i 行的值，我们就可以在线性时间复杂度内计算出第 i+1 行的值。
代码：

	 public static List<List<Integer>> generate(int numRows) {
	        List<List<Integer>> ret = new ArrayList<List<Integer>>();
	        for (int i = 0; i < numRows; ++i) {
	            List<Integer> row = new ArrayList<Integer>();
	            for (int j = 0; j <= i; ++j) {
	                if (j == 0 || j == i) {
	                    row.add(1);
	                } else {
	                    row.add(ret.get(i - 1).get(j - 1) + ret.get(i - 1).get(j));
	                }
	            }
	            ret.add((ArrayList<Integer>) row);
	        }
	        return ret;
	    }
	    public static void main(String[] args) {
		List<List<Integer>> list = new ArrayList<List<Integer>>();
		list = generate(5);
		for(List<Integer> al: list) {
			for(Integer i:al) {
				System.out.print(i+"\\t");
			}
			System.out.println();
		}
		System.out.println(list);
	}	

输出结果：