机器学习- 吴恩达Andrew Ng Week1 知识总结 Introduciton

Posted 2021-08-11 架构师易筋

Coursera课程地址

因为Coursera的课程还有考试和论坛，后续的笔记是基于Coursera
https://www.coursera.org/learn/machine-learning/home/welcome

1. 什么是机器学习？

提供了机器学习的两种定义。亚瑟·塞缪尔（Arthur Samuel）将其描述为：“让计算机无需明确编程即可学习的研究领域。” 这是一个较旧的非正式定义。

Tom Mitchell 提供了一个更现代的定义：“如果计算机程序在 T 中的任务上的性能（以 P 衡量）随着经验 E 提高，则称该计算机程序从经验 E 中学习某些类任务 T 和性能度量 P。 ”

例子：下棋。

• E = 玩多场下棋的经验

• T = 下棋的任务。

• P = 程序赢得下一场比赛的概率。

一般来说，任何机器学习问题都可以归为两大类之一：

1. 监督学习

2. 无监督学习。

1.1. 监督学习

在监督学习中，我们得到了一个数据集，并且已经知道我们的正确输出应该是什么样子，并且知道输入和输出之间存在关系。

监督学习问题分为“回归”和“分类”问题。在回归问题中，我们试图预测连续输出中的结果，这意味着我们试图将输入变量映射到某个连续函数。在分类问题中，我们试图在离散输出中预测结果。换句话说，我们试图将输入变量映射到离散类别中。这是对连续和离散数据的数学乐趣的描述。

示例 1：

给定有关房地产市场上房屋大小的数据，尝试预测它们的价格。价格作为规模的函数是一个连续的输出，所以这是一个回归问题。

我们可以把这个例子变成一个分类问题，通过输出关于房子是“高于还是低于要价”的输出。在这里，我们根据价格将房屋分为两个独立的类别。

示例 2：

(a) 回归 - 给定一张男/女的照片，我们必须根据给定的图片预测他/她的年龄。

(b) 分类——给定一张男/女的图片，我们必须预测他/她是高中、大学、研究生的年龄。另一个分类示例 - 银行必须根据某人的信用记录来决定是否向其提供贷款。

1.2 无监督学习

另一方面，无监督学习允许我们在几乎不知道结果应该是什么样子的情况下解决问题。我们可以从数据中推导出结构，而我们不一定知道变量的影响。

我们可以通过基于数据中变量之间的关系对数据进行聚类来推导出这种结构。

在无监督学习中，没有基于预测结果的反馈，即没有老师来纠正你。

例子：

聚类：收集 1000 篇关于美国经济的文章，并找到一种方法，将这些文章自动归为一小部分，这些文章通过不同的变量（例如词频、句子长度、页数等）在某种程度上相似或相关上。

非聚类：“鸡尾酒会算法”，它可以在杂乱的数据中找到结构（例如从鸡尾酒会上的声音网格中识别个人声音和音乐（https://en.wikipedia.org/wiki/ Cocktail_party_effect ) )。这是 Quora 上的答案，以增强您的理解。https://www.quora.com/What-is-the-difference-between-supervised-and-unsupervised-learning-algorithms

2. ML：一个变量的线性回归

模型表示
回想一下，在回归问题中，我们采用输入变量并尝试将输出拟合到连续的预期结果函数上。

具有一个变量的线性回归也称为“单变量线性回归”。

当您想从单个输入值 x预测单个输出值 y时，使用单变量线性回归。我们在这里进行监督学习，这意味着我们已经知道输入/输出的因果关系应该是什么。

假设函数
我们的假设函数具有一般形式：

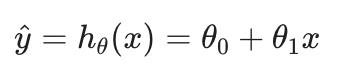
请注意，这类似于直线方程。我们给hθ(x)值 θ0 和 θ1 得到我们的估计输出y, 换句话说，我们正在尝试创建一个名为hθ这是试图将我们的输入数据（x）映射到我们的输出数据（y）。

例子：
假设我们有以下一组训练数据：

现在我们可以随机猜测我们的 hθ 功能： θ0 =2 和 θ1=2. 假设函数变为h(x)=2+2x.
因此，对于我们假设的输入 1，y 将是 4。这是 3。请注意，我们将尝试不同的值θ0 和 θ1 尝试通过映射在 xy 平面上的数据点找到提供最佳“拟合”或最具代表性的“直线”的值。

3. 成本函数

我们可以使用成本函数来衡量假设函数的准确性。这需要假设的所有结果的平均值（实际上是平均值的更高级版本），其中输入来自 x 的输入与实际输出 y 的比较。

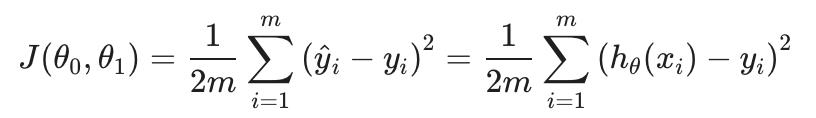
要把它拆开，它是 x/2 向量 在哪里 x向量是平方的平均值， hθ(xi) - yi或预测值与实际值之间的差异。

此函数也称为“平方误差函数”或“均方误差”。平均值减半(1/2m), 为方便计算梯度下降，因为平方函数的导数项将抵消 1/2 学期。

现在我们能够根据我们拥有的正确结果具体衡量我们的预测函数的准确性，以便我们可以预测我们没有的新结果。

如果我们尝试从视觉角度考虑，我们的训练数据集分散在 xy 平面上。我们正在尝试制作直线（定义为Hθ(x))通过这组分散的数据。我们的目标是获得最好的生产线。可能的最佳线应使散点与线的平均垂直距离平方最小。在最好的情况下，这条线应该穿过我们训练数据集的所有点。在这种情况下的价值 J(θ0, θ1)将是 0。

4. ML：梯度下降

所以我们有我们的假设函数，我们有一种方法来衡量它与数据的拟合程度。现在我们需要估计假设函数中的参数。这就是梯度下降的用武之地。

想象一下，我们根据其字段绘制我们的假设函数 θ0 和 θ1（实际上，我们将成本函数绘制为参数估计的函数）。这可能有点令人困惑；我们正在向更高的抽象层次发展。我们不是在绘制 x 和 y 本身，而是绘制我们假设函数的参数范围以及选择特定参数集所产生的成本。
我们把 θ0在 x 轴和θ1在 y 轴上，成本函数在垂直 z 轴上。我们图表上的点将是成本函数的结果，使用我们的假设和那些特定的 theta 参数。

当我们的成本函数在我们图中的坑的最底部时，即当它的值是最小值时，我们就会知道我们已经成功了。

我们这样做的方法是取我们的成本函数的导数（函数的切线）。切线的斜率是该点的导数，它将为我们提供前进的方向。我们在下降最快的方向上逐步降低成本函数，每一步的大小由参数α决定，称为学习率。

梯度下降算法为：

重复直到收敛：

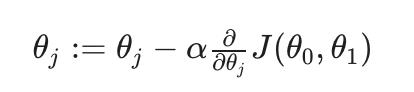
在哪里

          j=0,1 表示特征索引号。

直观地，这可以被认为是：

重复直到收敛：

4.1 线性回归的梯度下降

当专门应用于线性回归的情况时，可以推导出一种新形式的梯度下降方程。我们可以替换我们的实际成本函数和我们的实际假设函数并将方程修改为（公式的推导超出了本课程的范围，但可以在这里找到一个非常棒的公式）：


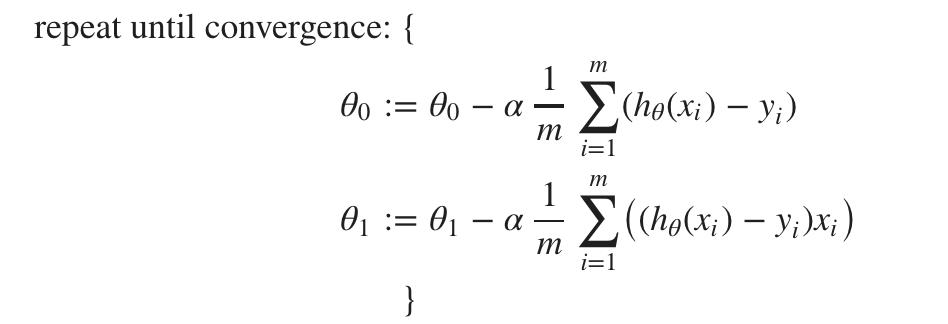
这一切的重点是，如果我们从对假设的猜测开始，然后重复应用这些梯度下降方程，我们的假设将变得越来越准确。

4.1.1 线性回归的梯度下降：视觉工作示例

有些人可能会发现以下视频 ( https://www.youtube.com/watch?v=WnqQrPNYz5Q ) 很有用，因为它可视化了随着误差函数减小而改进的假设。

5 ML：线性代数评论

可汗学院有优秀的线性代数教程 ( https://www.khanacademy.org/#linear-algebra )

参考

https://www.coursera.org/learn/machine-learning/resources/JXWWS