算法入门深度优先搜索（中等 - 第二题）LeetCode 46

Posted 2021-08-11 英雄哪里出来

🙉饭不食，水不饮，题必须刷🙉
还不会C语言，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？上简单题！ 🧡《C语言入门100例》🧡
LeetCode 太简单？大神盘他！ 🌌《夜深人静写算法》🌌

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识

一、题目

1、题目描述

  给定一个 不含重复数字 的长度小于 7 的数组 $nums$ ，返回其 所有可能的全排列。
  样例：$nums=[1,2,3]$，输出$[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]$

2、基础框架

• c++ 版本给出的基础框架代码如下:

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
    }
};

• 定义一个函数permute，函数的参数是一个vector，代表的是一个数组；
• 返回值是vector<vector<int>>可以理解成vector<T>，其中T代表vector的元素，并且这个元素是另一个vector<int>。当然，可以嵌套的实现三维数组，甚至更高维的数组。
  

3、原题链接

LeetCode 46. 全排列

二、解题报告

1、思路分析

• 全排列的种数是 $n!$，这是最典型的深搜问题。我们可以把 $n$ 个数两两建立无向边（即任意两个结点之间都有边，也就是一个 $n$ 个结点的完全图），然后对每个点作为起点，分别做一次深度优先搜索，当所有点都已经标记时，输出当前的搜索路径，就是其中一个排列；
• 这里需要注意的是，回溯的时候需要将原先标记的点的标记取消，否则只能输出一个排列。
• 如下图，代表的是3个数的图表示：
  
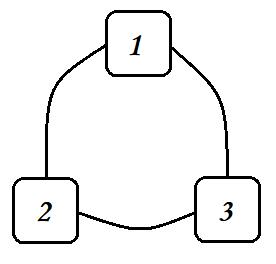
• 3个数的全排列的深度优先搜索空间树如下图所示：
  
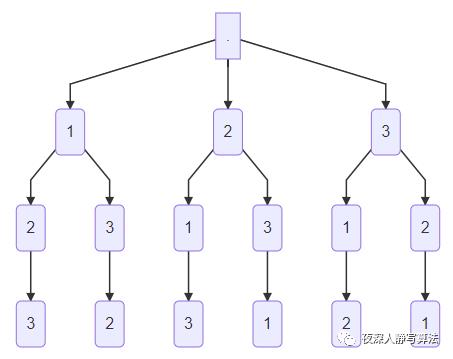
• 关于深度优先搜索的更深入内容，可以参考这篇文章：夜深人静写算法（一）- 搜索入门。

2、时间复杂度

• 由于每次访问后会将标记过的节点标记回来，所以时间复杂度就是排列数，即 $O(n!)$。

3、代码详解

class Solution {
    int hash[6];

    void dfs(int dep, int maxdep, vector<int>& nums, vector<vector<int>>& ans, vector<int>& st) {                                                            // (1)
        if(dep == maxdep) {
            ans.push_back( st );                             // (2)
            return ;
        }

        for(int i = 0; i < maxdep; ++i) {                    
            if(!hash[i]) {                                   // (3)
                hash[i] = 1;                                
                st.push_back(  nums[i] );                   
                dfs(dep + 1, maxdep, nums, ans, st);         // (4)
                st.pop_back();                               // (5)
                hash[i] = 0;                                 // (6)
            }
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> ans;            
        memset(hash, 0, sizeof(hash));        
        vector<int> st; 
        dfs(0, nums.size(), nums, ans, st);     
        return ans;
    }
};

• $(1)$ dep代表本地递归访问第几个节点，maxdep代表递归的层数，vector<int>& nums则代表原始输入数组，vector<vector<int>>& ans代表结果数组，vector<int>& st代表存储当前搜索结果的栈；
• $(2)$ dep == maxdep代表一次全排列访问，这时候得到一个可行解，放入结果数组中；
• $(3)$ 如果节点 $i$ 未访问，则将第 $i$ 个节点的值塞入搜索结果栈，并且用hash数组标记已访问；
• $(4)$ 继续递归调用下一层；
• $(5)$ 将栈顶元素弹出，代表本次访问的回溯；
• $(6)$ 取消数组标记；

---

三、本题小知识

利用深度优先搜索，可以用来求全排列问题。

---