计算机组成与设计---硬件/软件接口---计算机的算术运算

Posted 2021-08-11 FANCY PANDA

3.1 加和减法

整数加法
例子: 7 + 6

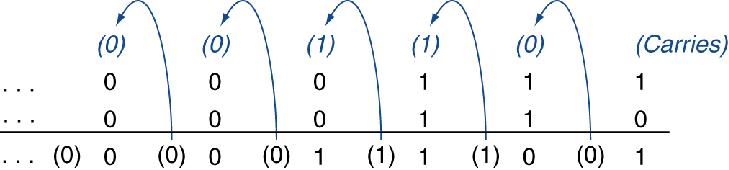
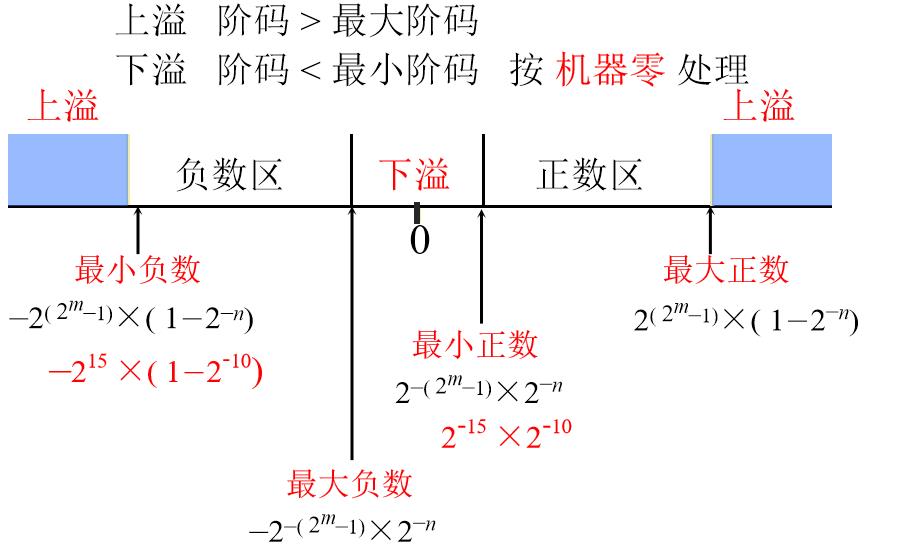
• 结果超出表示范围就会发生溢出(定义)
• • 正数和负数相加，不会溢出
• • 两个正数相加
• • • 符号位为1，表示发生溢出
• • 两个负数相加
• • • 符号位为0，表示发生溢出

整数减法
减法：加上加数的负值
例如: 7 – 6 = 7 + (–6)

• 结果超出范围就会溢出
• • 相同同符号位相减，不会溢出
• • 一个负数减去一个正数
• • • 符号位为0，表示发生溢出
• • 一个正数减去一个负数
• • • 符号位为1，表示发生溢出

在什么情况下可能产生溢出？

• 数A，1位符号SA
• 数B，1位符号SB
• 结果符号Sf
• 符号位进位Cf（没有）
• 尾数最高位进位C
  

3.2 乘法

3.2.1 顺序的乘法算法和硬件

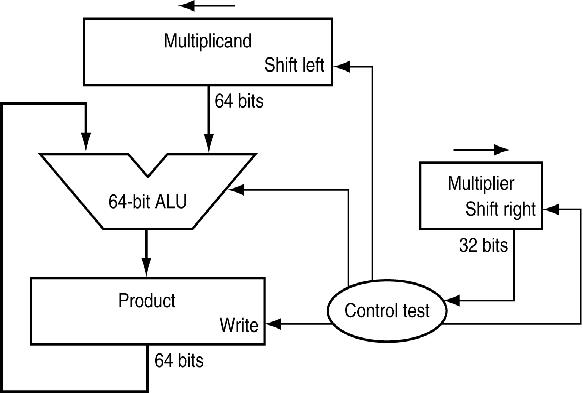
改进后的乘法器：

• 操作并行: add/shift
• 一个时钟完成一次积:频率较低
  

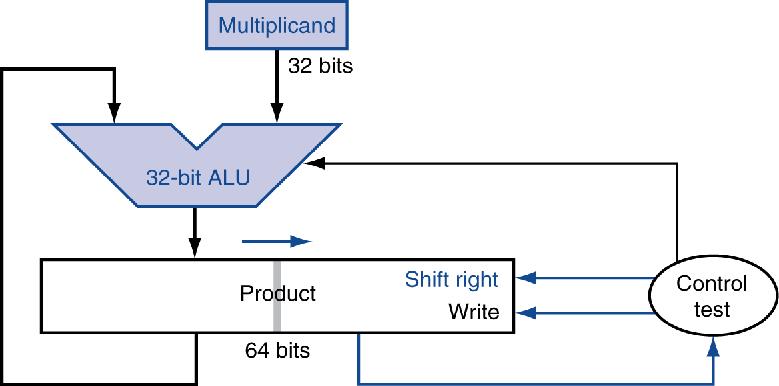
3.2.3 更快速的乘法.

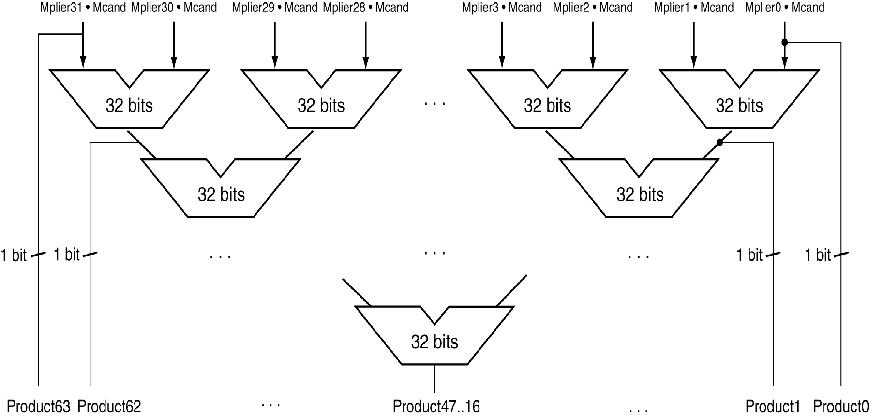
• 使用多个加法器,成本/效率的折衷
• 可以流水执行:几个加法可以同步执行（不同的阶段）

3.2.4 MIPS中的乘法

2个32位的寄存器来保存积（积是64位）

• HI: 高32 bits
• LO: 低32-bits

指令

• mult rs, rt / multu rs, rt
• • 64-bit product in HI/LO
• mfhi rd / mflo rd
• • 传送 HI/LO 到 rd
• • 可以检查HI的值来判断结果是否超过32位
• mul rd, rs, rt
• • 低32位存入rd寄存器

3.3 除法

3.3.1除法算法及其硬件结构

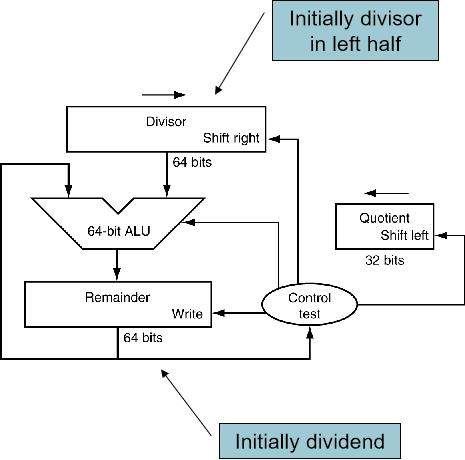
改进后的除法器

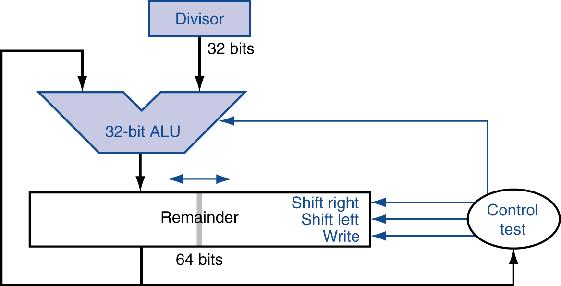
• 一个时钟周期做一次减法
• 和乘法器类似
• • 乘法和除法可以共用同样的硬件

3.3.2MIPS中的除法

HI/LO寄存器存储结果

• HI: 32位余数
• LO: 32位商
  指令
• div rs, rt / divu rs, rt
• 不会溢出和除0检查
• • 如果需要，软件必须进行检查
• 使用mfhi, mflo指令 访问结果

3.4浮点运算

3.4.1浮点表示

2种精度
单精度(32-bit)
双精度 (64-bit)

• S: 符号位(0 为 非负数, 1 为 负数)
• 有效位的规格化: 1.0 ≤ |有效位| < 2.0
• • 数前总有一个前导的1，此外作为隐含位可以不表示。
• • 有效位是 “1. 尾数”
• 阶码: 移码表示: 真实的指数 + 偏移
• • Ensures exponent is unsigned
• • Single: 偏移= 127; Double: 偏移= 1203

3.4.2浮点加法

以一个4位的十进制数为例：9.999 × 10^1 + 1.610 × 10^–1

1. 对阶
   把小阶的值调整到和大阶一致(-1调整到1)
   9.999 × 10 ^ 1 + 0.016 × 10 ^ 1
2. 尾数相加
   9.999 × 10^ 1 + 0.016 × 101 = 10.015 × 10^1
3. 结果规格化& 检查是否溢出
   1.0015 × 10^2
4. 进行必要的舍入处理
   1.002 × 10^2

现在计算一个4位的二进制数1.000(2) × 2^–1 + –1.110(2) × 2^–2 (0.5 + –0.4375)

1. 对接
   小阶对大阶
   1.000(2) × 2^–1 + –0.111(2) × 2 ^–1
2. 尾数相加
   1.000(2) × 2^–1 + –0.111(2) × 2 ^ –1 = 0.001(2) × 2 ^–1
3. 规格化 & 检查溢出
   1.000(2) × 2^–4, with no over/underflow
4. 进行必要的舍入
   1.000(2) × 2^–4 (no change) = 0.0625
   

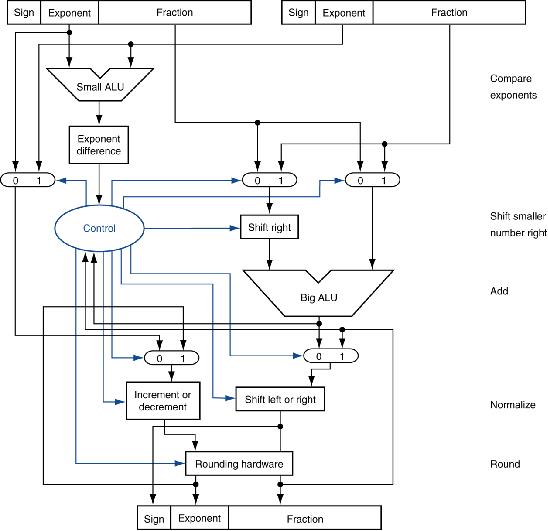
3.4.3浮点乘法

以一个4位的十进制乘法为例1.110 × 10^10 × 9.200 × 10^–5

1. 指数相加
   如果指数有偏移，还需要减去多加的偏移值
   新指数 = 10 + –5 = 5
2. 有效位相乘
   1.110 × 9.200 = 10.212  10.212 × 10^5
3. 规格化，同时检查上溢和下溢
   1.0212 × 10^6
4. 舍入，可能还需要进一步规格化
   1.021 × 10^6
5. 计算符号位
   +1.021 × 10^6

下面是一个4位的二进制数的例子1.000(2) × 2^–1 × –1.110(2) × 2^–2 (0.5 × –0.4375)

1. 阶码相加
   无偏移: –1 + –2 = –3
   有偏移: (–1 + 127) + (–2 + 127) = –3 + 254 – 127 = –3 + 127
2. 有效位相乘
   1.000(2) × 1.110(2) = 1.1102 为 1.110(2) × 2^–3
   3.规格化，同时检查上溢和下溢
   1.110(2) × 2^–3 无溢出，也不需规格化
   4.舍入，可能还需要进一步规格化
   1.110(2) × 2^–3 (no change)
   5.计算符号位: +ve × –ve 为 –ve
   –1.110(2) × 2^–3 = –0.21875

3.4.4MIPS中的浮点指令

• 浮点数使用协处理器
• • 通过ISA相连的附属处理器
• 独立的浮点寄存器
• • 32个单精度: $f0, $f1, … $f31
• • 配对为双精度: $ f0/$ f1, $ f 2/$ f3, …
• • • Release 2 of MIPs ISA supports 32 × 64-bit FP reg’s
• 浮点指令只操作浮点寄存器
• • 程序通常不会在浮点寄存器上进行整数操作，或在整数寄存器上进行浮点操作
• • 因此可以提供更多的寄存器，而不影响指令的长度
• 浮点数读取、存储指令
• • lwc1, ldc1, swc1, sdc1
• • • e.g., ldc1 $ f8, 32($ sp)
• 单精度
• • add.s, sub.s, mul.s, div.s
• • • -e.g., add.s $f0, $f1, $f6
• 双精度
• • add.d, sub.d, mul.d, div.d
• • • e.g., mul.d $f4, $f4, $f6
• 比较
• • c.xx.s, c.xx.d (xx is eq, lt, le, …)
• • Sets or clears FP condition-code bit
• • • e.g. c.lt.s $f3, $f4
• 分支
• • bc1t, bc1f
• • • e.g., bc1t TargetLabel

计算机组成与设计—硬件/软件接口—计算机概要与技术

计算机组成与设计—硬件/软件接口—指令: 计算机的语言

计算机组成与设计—硬件/软件接口—处理器

计算机组成与设计—硬件/软件接口—大容量和高速度:开发存储器层次结构