Week2 腾讯2019 暑期实习提前批笔试 —— ACWing 569. 猜拳游戏

Posted 2021-08-11 JohnnyLin00

【题目描述】

569. 猜拳游戏
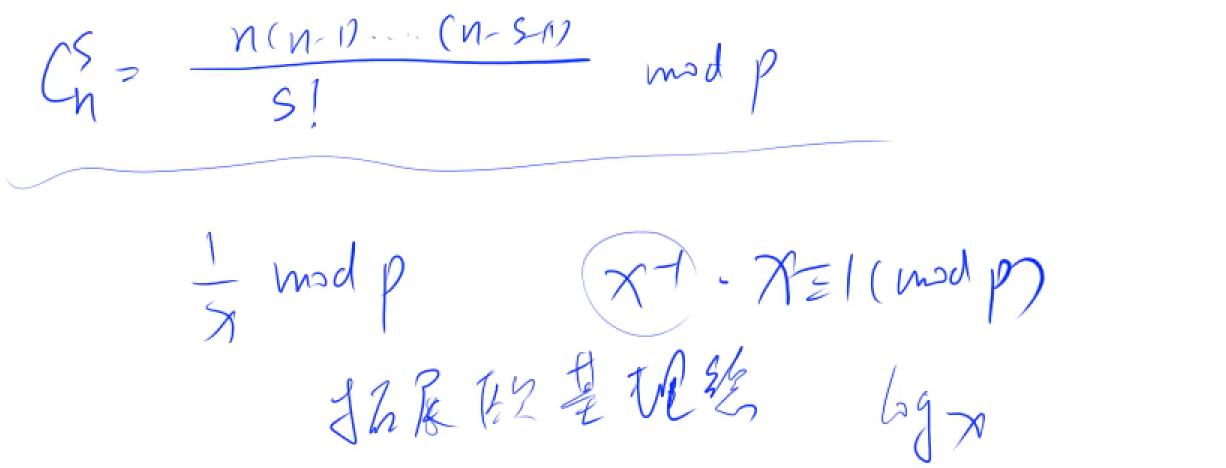x/y (mod p) 等于x乘以 y的模逆元，而y的模逆元等于 y^(p - 1),可以使用快速幂计算

【思路】

目标： 计算 C(n, s) * 2 ^( n - s) % p
上式C(n, s) * 2 ^( n - s) % p =  A(n,s) /s! * 2 ^( n - s) % p

在计算阶乘的过程中可能出现数据范围溢出  
根据费马小定理可以转化为 模逆元计算   求 1/s!(mod p)  实际上就是 求 s^(p -2) ( 要求  s % p = 1)
因此：C(n,s) % p = A(n,s)%p * (s!^p-2)

import java.util.Scanner;

public class Main{
    
    static long mod = 1000000007;
    public static long quick_pow(long x, long n){
        
        long res = 1;
        while( n > 0){
            if( (n & 1) == 1) res = x * res  % mod;
            n >>= 1;  
            x = x * x % mod;
            
        }
        return res % mod;
    }
    public static void main(String args[]){
        Scanner reader = new Scanner(System.in);
        int n = reader.nextInt(), s = reader.nextInt();
        String str = reader.next();// 序列没有用到
        if( s > n ) System.out.println(0);
        else{
            //C(n,s) % p = A(n,s)%p * (s!^p-2)
            long A = 1,  S = 1, ans = 1;
            for(int i = n; i >= n - s +1; i --) A = A * i % mod;
            for(int i = s; i >= 1; i --) S = S * i % mod;
            S = quick_pow(S, mod -2);
            // 计算 2 ^( n - s) % p
            long t = quick_pow(2, n - s) ;
            System.out.println(  A * S % mod * t % mod );
            
        }
    }
}