史诗级干货长文线性回归算法

Posted 2021-08-11 ZSYL

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了史诗级干货长文线性回归算法相关的知识，希望对你有一定的参考价值。

线性回归算法

前言
1. 线性回归简介
2. 线性回归API初步使用
3. 数学:求导
4. 线性回归的损失和优化
5. 梯度下降法介绍
6. 线性回归API再介绍
7. 案例：波士顿房价预测
8. 欠拟合和过拟合
9. 正则化线性模型
10. 线性回归的改进-岭回归
11. 模型的保存和加载

前言

学习目标：

掌握线性回归的实现过程
应用LinearRegression或SGDRegressor实现回归预测
知道回归算法的评估标准及其公式
知道过拟合与欠拟合的原因以及解决方法
知道岭回归的原理及与线性回归的不同之处
应用Ridge实现回归预测
应用joblib实现模型的保存与加载

1. 线性回归简介

1.1 线性回归应用场景

房价预测
销售额度预测
贷款额度预测

举例：

在这里插入图片描述

1.2 什么是线性回归

1.2.1 定义与公式

线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归

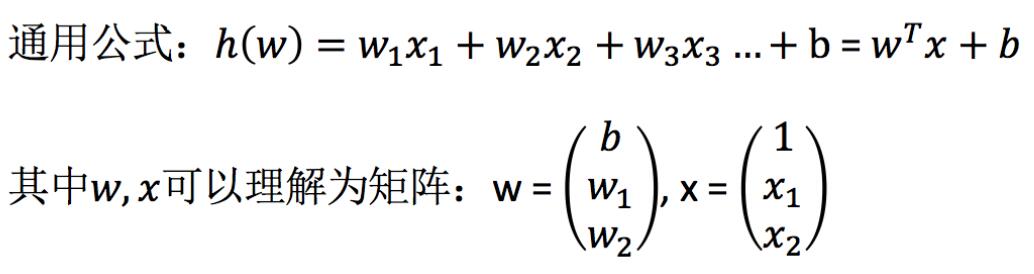
在这里插入图片描述

线性回归用矩阵表示举例

在这里插入图片描述

那么怎么理解呢？我们来看几个例子

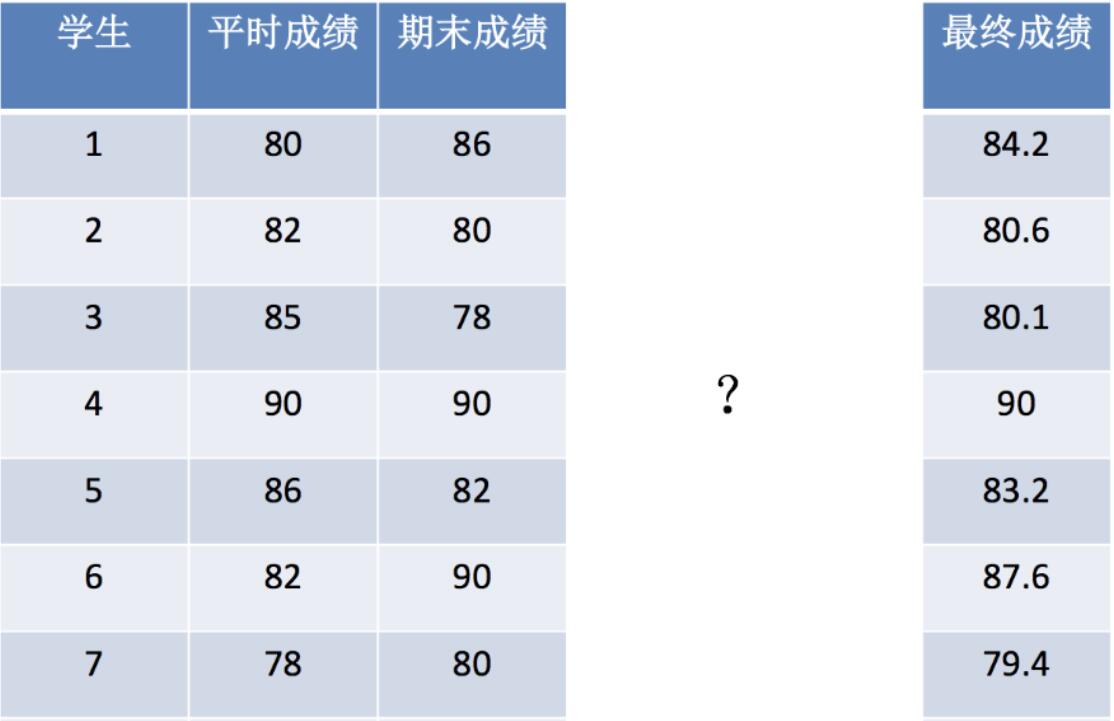
期末成绩：0.7×考试成绩+0.3×平时成绩
房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

上面两个例子，我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型。

1.2.2 线性回归的特征与目标的关系分析

线性回归当中主要有两种模型，一种是线性关系，另一种是非线性关系。在这里我们只能画一个平面更好去理解，所以都用单个特征或两个特征举例子。

线性关系

单变量线性关系：

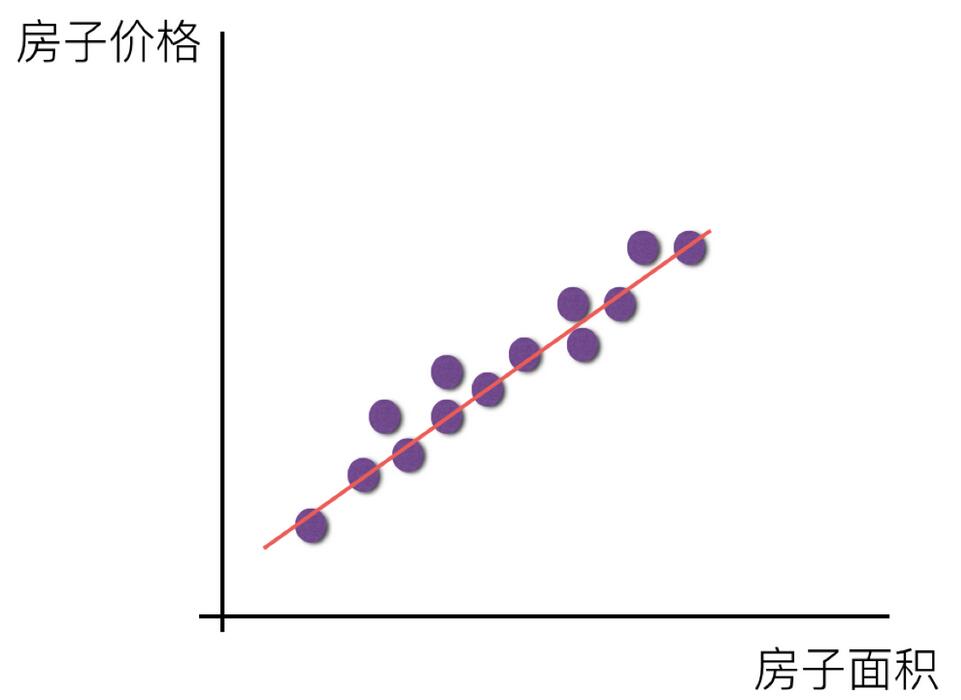
在这里插入图片描述

多变量线性关系

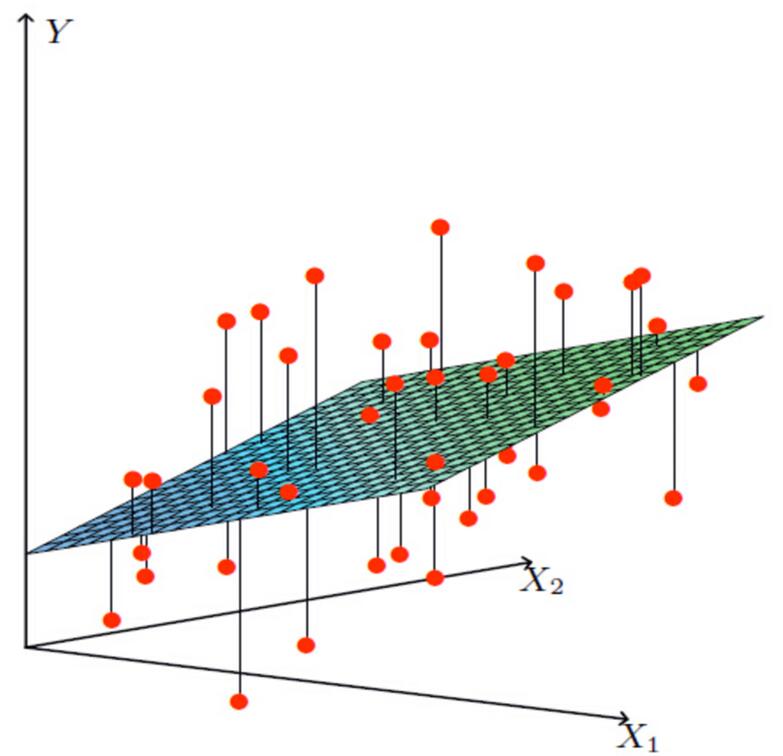
在这里插入图片描述

注释：单特征与目标值的关系呈直线关系，或者两个特征与目标值呈现平面的关系
更高维度的我们不用自己去想，记住这种关系即可

非线性关系

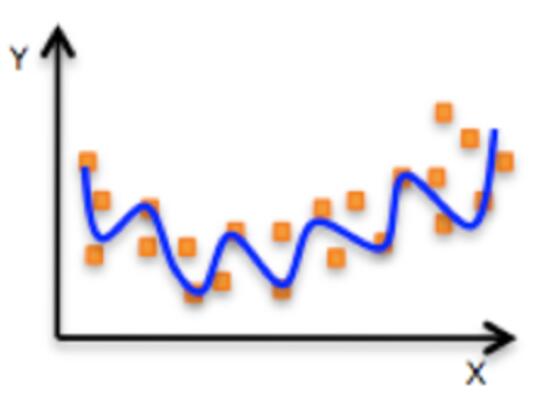
在这里插入图片描述

线性回归的定义
- 利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式
线性回归的分类
- 线性关系
- 非线性关系

2. 线性回归API初步使用

2.1 线性回归API

sklearn.linear_model.LinearRegression()
- LinearRegression.coef_：回归系数

2.2 举例

在这里插入图片描述

2.2.1 步骤分析

1.获取数据集
2.数据基本处理（该案例中省略）
3.特征工程（该案例中省略）
4.机器学习
5.模型评估（该案例中省略）

2.2.2 代码过程

导入模块

from sklearn.linear_model import LinearRegression

构造数据集

x = [[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]

机器学习-- 模型训练

# 实例化API
estimator = LinearRegression()
# 使用fit方法进行训练
estimator.fit(x,y)

estimator.coef_

estimator.predict([[100, 80]])  # 86

3. 数学:求导

3.1 常见函数的导数

在这里插入图片描述

3.2 导数的四则运算

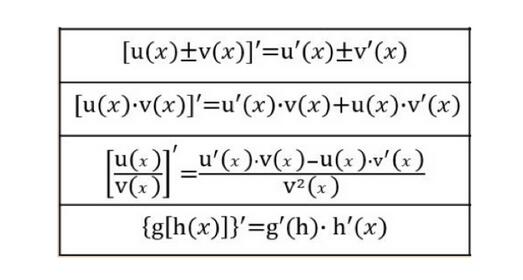
在这里插入图片描述

3.3 练习

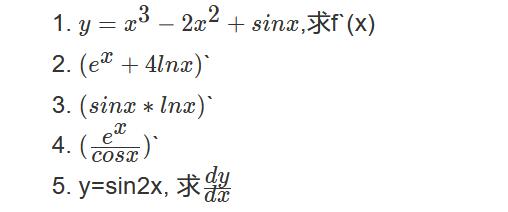
在这里插入图片描述
答案：

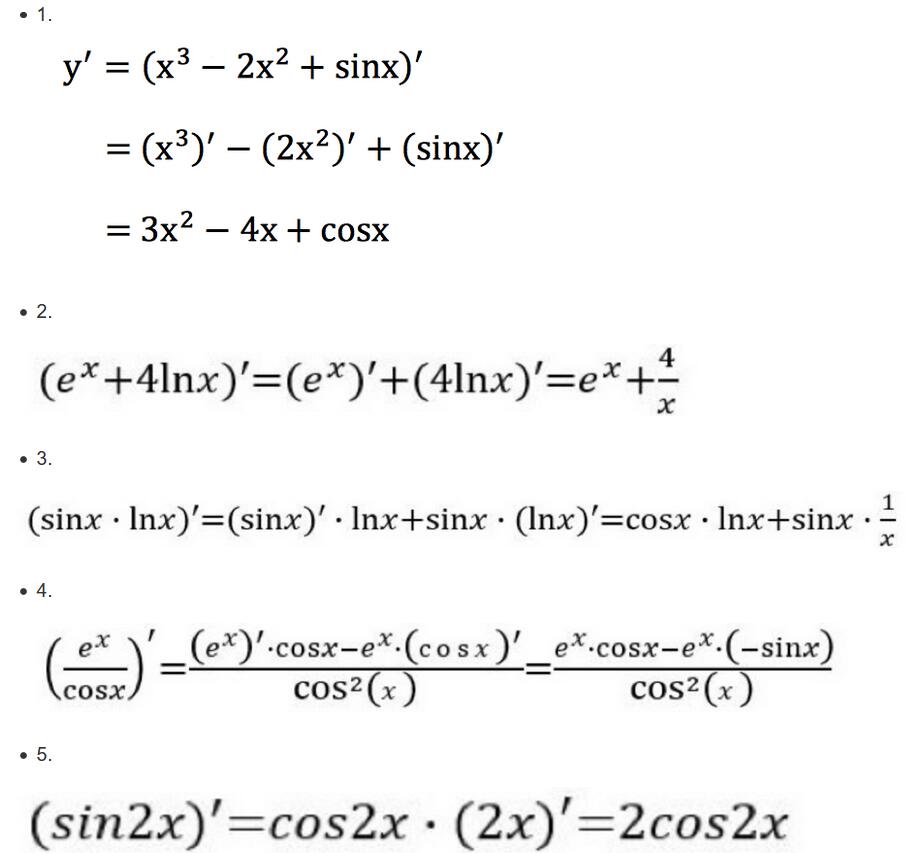
在这里插入图片描述

3.4 矩阵（向量）求导

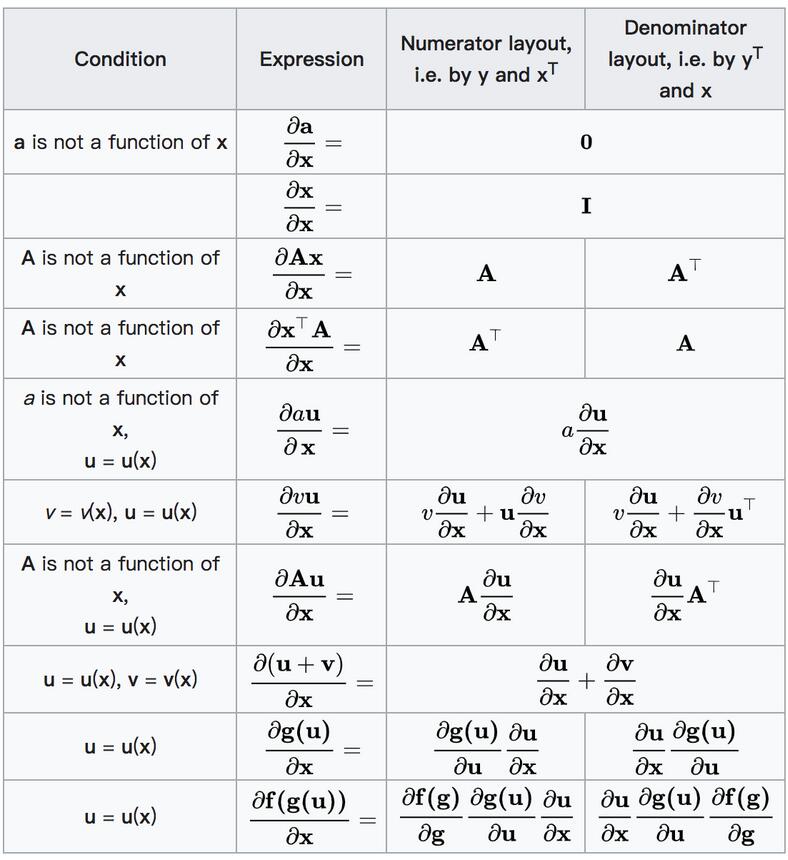
在这里插入图片描述
参考链接：https://en.wikipedia.org/wiki/Matrix_calculus#Scalar-by-vector_identities

4. 线性回归的损失和优化

学习目标

知道线性回归中损失函数
知道使用正规方程对损失函数优化的过程
知道使用梯度下降法对损失函数优化的过程

4.1 损失函数

4.2 优化算法

4.2.1 正规方程

4.2.1 梯度下降

请参考：机器学习】线性回归的损失和优化

5. 梯度下降法介绍

学习目标

知道全梯度下降算法的原理
知道随机梯度下降算法的原理
知道随机平均梯度下降算法的原理
知道小批量梯度下降算法的原理

请参考: 【机器学习】梯度下降法（超详解）

6. 线性回归API再介绍

sklearn.linear_model.LinearRegression(fit_intercept=True)
- 通过正规方程优化
- 参数
  - fit_intercept：是否计算偏置
- 属性
  - LinearRegression.coef_：回归系数
  - LinearRegression.intercept_：偏置
sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)
- SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
- 参数：
  - loss:损失类型
    - loss=”squared_loss”: 普通最小二乘法
  - fit_intercept：是否计算偏置
  - learning_rate : string, optional
    - 学习率填充
    - ‘constant’: eta = eta0
    - ‘optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
    - ‘invscaling’: eta = eta0 /
      - pow(t, power_t)
    - 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
- 属性：
  - SGDRegressor.coef_：回归系数
  - SGDRegressor.intercept_：偏置

sklearn提供给我们两种实现的API，可以根据选择使用

小结

正规方程
- sklearn.linear_model.LinearRegression()
梯度下降法
- sklearn.linear_model.SGDRegressor(）

7. 案例：波士顿房价预测

学习目标

通过案例掌握正规方程和梯度下降法api的使用

请参考:【线性回归】案例：波士顿房价预测

8. 欠拟合和过拟合

学习目标

掌握过拟合、欠拟合的概念
掌握过拟合、欠拟合产生的原因
知道什么是正则化，以及正则化的分类

请参考:【机器学习】欠拟合和过拟合

请参考:【机器学习】维灾难

9. 正则化线性模型

学习目标

知道正则化中岭回归的线性模型
知道正则化中lasso回归的线性模型
知道正则化中弹性网络的线性模型
了解正则化中early stopping的线性模型
Ridge Regression 岭回归
Lasso 回归
Elastic Net 弹性网络
Early stopping

9.1 Ridge Regression (岭回归，又名 Tikhonov regularization)

岭回归是线性回归的正则化版本，即在原来的线性回归的 cost function 中添加正则项（regularization term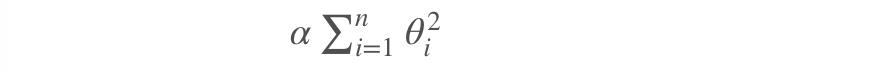）: 在这里插入图片描述

以达到在拟合数据的同时，使模型权重尽可能小的目的,岭回归代价函数:
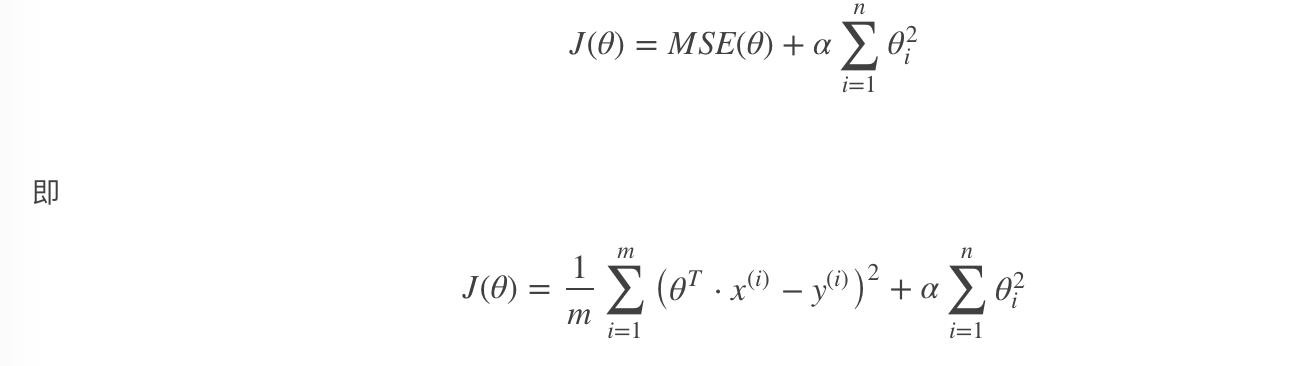
在这里插入图片描述

α=0：岭回归退化为线性回归

9.2 Lasso Regression(Lasso 回归)

Lasso回归是线性回归的另一种正则化版本，正则项为权值向量的ℓ1范数。

Lasso回归的代价函数：

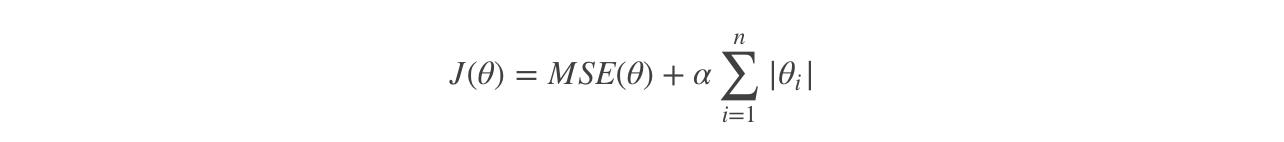
在这里插入图片描述

【注意】

Lasso Regression 的代价函数在 θi=0处是不可导的.
解决方法：在θi=0处用一个次梯度向量(subgradient vector)代替梯度，如下式
Lasso Regression 的次梯度向量

Lasso Regression 有一个很重要的性质是：倾向于完全消除不重要的权重。

例如：当α 取值相对较大时，高阶多项式退化为二次甚至是线性：高阶多项式特征的权重被置为0。

也就是说，Lasso Regression 能够自动进行特征选择，并输出一个稀疏模型（只有少数特征的权重是非零的）。

9.3 Elastic Net (弹性网络)

弹性网络在岭回归和Lasso回归中进行了折中，通过 混合比(mix ratio) r 进行控制：

r=0：弹性网络变为岭回归
r=1：弹性网络便为Lasso回归

弹性网络的代价函数：
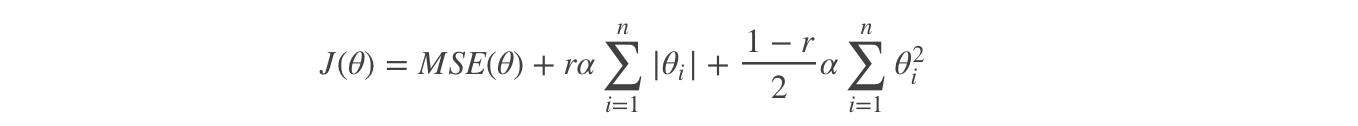
在这里插入图片描述

一般来说，我们应避免使用朴素线性回归，而应对模型进行一定的正则化处理，那如何选择正则化方法呢？

小结：

常用：岭回归
假设只有少部分特征是有用的：
- 弹性网络
- Lasso
- 一般来说，弹性网络的使用更为广泛。因为在特征维度高于训练样本数，或者特征是强相关的情况下，Lasso回归的表现不太稳定。
api:
- from sklearn.linear_model import Ridge, ElasticNet, Lasso

9.4 Early Stopping

Early Stopping 也是正则化迭代学习的方法之一。

其做法为：在验证错误率达到最小值的时候停止训练。

9.5 小结

Ridge Regression 岭回归
- 就是把系数添加平方项
- 然后限制系数值的大小
- α值越小，系数值越大，α越大，系数值越小
Lasso 回归
- 对系数值进行绝对值处理
- 由于绝对值在顶点处不可导，所以进行计算的过程中产生很多0，最后得到结果为：稀疏矩阵
Elastic Net 弹性网络
- 是前两个内容的综合
- 设置了一个r,如果r=0–岭回归；r=1–Lasso回归
Early stopping
通过限制错误率的阈值，进行停止

10. 线性回归的改进-岭回归

10.1 API

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
- 具有l2正则化的线性回归
- alpha:正则化力度，也叫 λ
  - λ取值：0~1 1~10
- solver:会根据数据自动选择优化方法
  - sag:如果数据集、特征都比较大，选择该随机梯度下降优化
- normalize:数据是否进行标准化
  - normalize=False:可以在fit之前调用- - - - preprocessing.StandardScaler标准化数据
- Ridge.coef_:回归权重
- Ridge.intercept_:回归偏置

Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)

sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
- 具有l2正则化的线性回归，可以进行交叉验证
- coef_:回归系数

class _BaseRidgeCV(LinearModel):
    def __init__(self, alphas=(0.1, 1.0, 10.0),
                 fit_intercept=True, normalize=False,scoring=None,
                 cv=None, gcv_mode=None,
                 store_cv_values=False):

10.2 观察正则化程度的变化，对结果的影响？

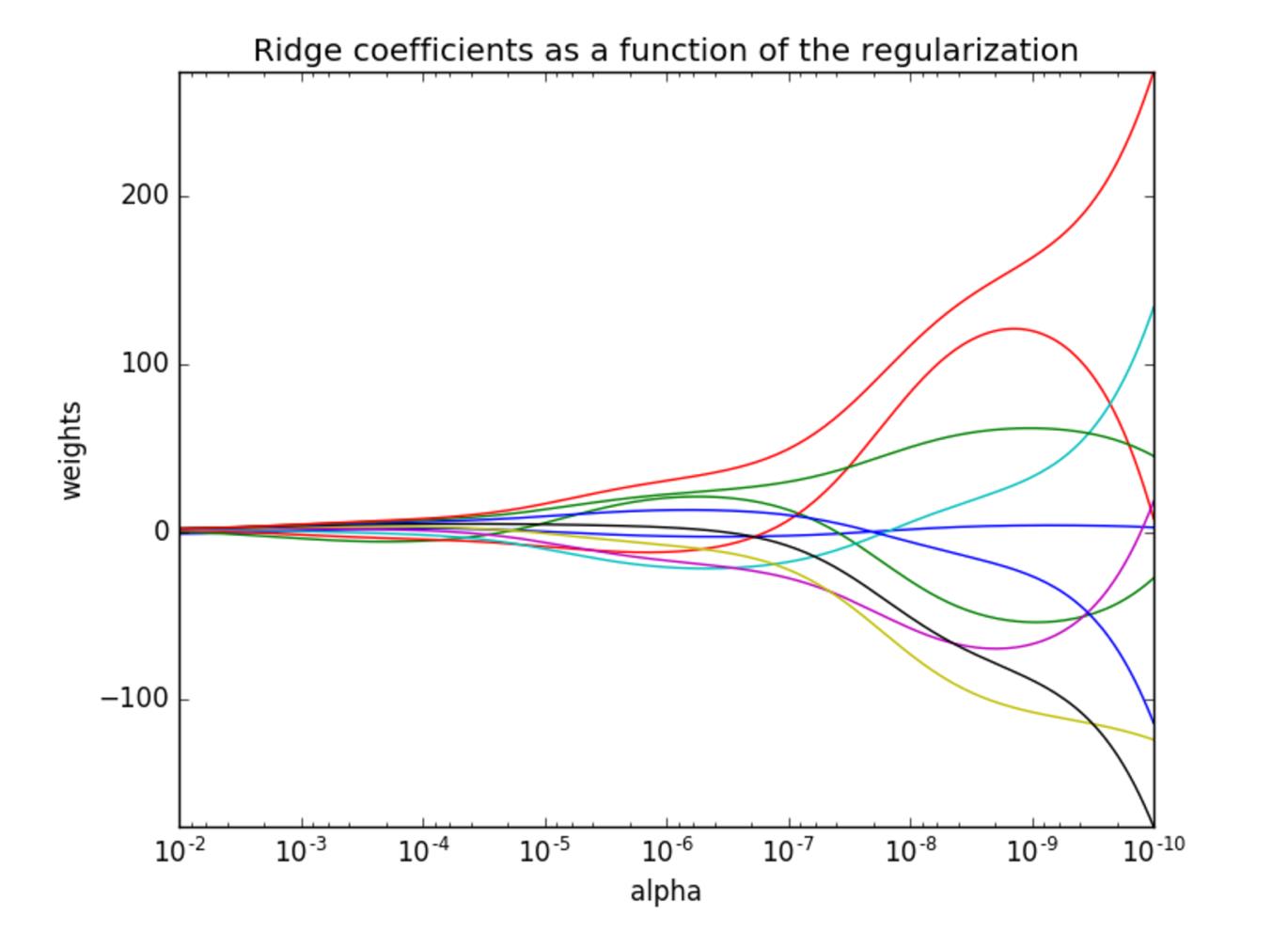
在这里插入图片描述

正则化力度越大，权重系数会越小
正则化力度越小，权重系数会越大

10.3 波士顿房价预测

def linear_model3():
    """
    线性回归:岭回归
    :return:
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(岭回归)
    estimator = Ridge(alpha=1)
    # estimator = RidgeCV(alphas=(0.1, 1, 10))
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\\n", y_predict)
    print("模型中的系数为:\\n", estimator.coef_)
    print("模型中的偏置为:\\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\\n", error)

10.4 小结

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
- 具有l2正则化的线性回归
- alpha – 正则化
  - 正则化力度越大，权重系数会越小
  - 正则化力度越小，权重系数会越大
- normalize
  默认封装了，对数据进行标准化处理

11. 模型的保存和加载

11.1 sklearn模型的保存和加载API

from sklearn.externals import joblib
- 保存：joblib.dump(estimator, ‘test.pkl’)
- 加载：estimator = joblib.load(‘test.pkl’)

高版本的sklearn需要单独安装joblib

11.2 线性回归的模型保存加载案例

def load_dump_demo():
    """
    模型保存和加载
    :return:
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(岭回归)
    # # 4.1 模型训练
    # estimator = Ridge(alpha=1)
    # estimator.fit(x_train, y_train)
    #
    # # 4.2 模型保存
    # joblib.dump(estimator, "./data/test.pkl")

    # 4.3 模型加载
    estimator = joblib.load("./data/test.pkl")

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\\n", y_predict)
    print("模型中的系数为:\\n", estimator.coef_)
    print("模型中的偏置为:\\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\\n", error)

11.3 小结

sklearn.externals import joblib
- 保存：joblib.dump(estimator, 'test.pkl')
- 加载：estimator = joblib.load('test.pkl')
- 注意：
  - 1.保存文件，后缀名是.pkl
  - 2.加载模型是需要通过一个变量进行承接

加油!

感谢!

努力!

以上是关于史诗级干货长文线性回归算法的主要内容，如果未能解决你的问题，请参考以下文章

史诗级干货长文支持向量机

史诗级干货长文集成学习进阶（XGBoost & lightGBM）