jzoj3523NOIP2013模拟11.7A组树上倍增JIH的玩偶(tree)

Posted 2021-08-10 SSL_ZZL

【NOIP2013模拟11.7A组】JIH的玩偶

• 题面
• • Description
  • Input
  • Output
  • Sample Input
  • Sample Output
  • Data Constraint
• 解题思路
• Code

题面

Description

JIH的玩具厂设立以来，发展了一张销售关系网。这张网以玩具厂为总代理（根），构成一颗树。每个节点都代表一个客户，且每个节点都有重要度ai。JIH想将这些客户划成若干类别，当然同一类的客户重要度相差太大总是不妥。所以JIH决定先进行市场调研。JIH会选择两个客户X，从X向根走一共k个节点进行调查。调查的结果是这条路径上重要程度相差最大的两个客户的差值是多少。因为特殊需要，要求重要度大的客户必须在重要度小的客户后面（顺序为X到根，若序列为递减，则输出0，详情见样例）。

Input

第一行一个整数N 表示N个客户
第二行N个整数Ai 表示N个客户的重要程度（工厂是1）
第三行开始 共N-1行 每行2个整数 x,y 表示x的父亲是y
接着一行一个正整数Q，表示Q次调研
接着Q行，每行两个整数X，K。含义见题目表述。

Output

Q行，每行一个正整数，含义见题目描述。

Sample Input

6
5 6 1 7 5 2
2 1
3 1
4 2
5 2
6 3
3
4 3
6 2
6 3

Sample Output

0
0
4

Data Constraint

30% 的数据中N,Q<=1000
100%的数据中N,Q<=200000 Ai<=1000000

---

解题思路

aaaaaaa，我是真的不会树上倍增aaaaa

设[i][j]为第i个节点向上$2^j$步

1. fa[][]表示父亲节点
2. minn[][]表示这一段最小的点
3. maxn[][]表示这一段最大的点
4. ans[][]表示这一段的答案（即最大点 - 最小点）
5. pd[][]表示这一段是否合法（不合法：序列递减，输出0）

先把这几个预处理出来（具体看程序）
然后找答案时倍增往上跳（具体看程序）

（这图很重要）

---

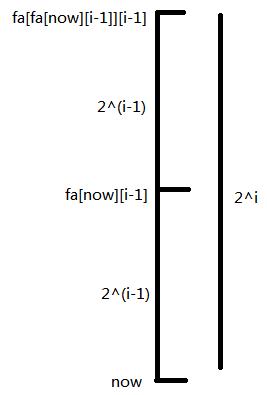
Code

#include <iostream>
#include <cstring>
#include <cstdio>

using namespace std;

struct DT{
	int to, next;
}a[200100];
int n, x, y, m, num, maxn[200100][30], minn[200100][30];
int fa[200100][30], ans[200100][30], pd[200100][30];
int lg[200100], head[200100], dep[200100], s[200100];
void add(int x, int y) {
	a[++num] = (DT){y, head[x]};
	head[x] = num;
}

void init_lg() {
	for(int i = 1; i <= n; i++)
		lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
}

void init_dfs(int now, int f) {
	dep[now] = dep[f] + 1;
	fa[now][0] = f;
	minn[now][0] = min(s[now], s[f]);
	maxn[now][0] = max(s[now], s[f]);
	if(s[now] <= s[f]) {
		pd[now][0] = 1; 
		ans[now][0] = s[f] - s[now];
	}
	for(int i = 1; i <= lg[dep[now]] - 1; i++) {
		fa[now][i] = fa[fa[now][i - 1]][i - 1];
		//2^i的父亲就是上半段的开头节点，具体看图
		minn[now][i] = min(minn[now][i - 1], minn[fa[now][i - 1]][i - 1]);
		//一整段的最小值=min（下半段最小值，上半段最小值）
		maxn[now][i] = max(maxn[now][i - 1], maxn[fa[now][i - 1]][i - 1]);
		//一整段的最大值=max（下半段最大值，上半段最大值）
		
		ans[now][i] = maxn[fa[now][i - 1]][i - 1] - minn[now][i - 1];
		//最大值在上半段，最小值在下半段
		ans[now][i] = max(ans[now][i], ans[fa[now][i - 1]][i - 1]);
		//最大值和最小值在上半段
		ans[now][i] = max(ans[now][i], ans[now][i - 1]);
		//最大值和最小值在下半段
		
		if(pd[now][i - 1] || pd[fa[now][i - 1]][i - 1])
		//只要有一段是不合法的，那么这一整个序列就不是递减的
			pd[now][i] = 1;
	}
	for(int i = head[now]; i; i = a[i].next)
			init_dfs(a[i].to, now); 
}

int work(int x, int k) {
	if(k == 1)return 0;
	int y = dep[x] - k + 1, hew = 0x7fffffff, flag = 0, now = 0;
	while(dep[x] > y) {
		int i = lg[dep[x] - y] - 1;
		if(pd[x][i]) flag = 1;
		now = max(now, ans[x][i]);
		//直接用答案，dep[x] + 2 ^ i ≤ y
		now = max(now, maxn[x][i] - hew);
		//y点并不刚刚好在2^a的地方上，就需要不断更新最小值来求
		hew = min(hew, minn[x][i]);  //更新最小值
		x = fa[x][i];  //不断往上跳
	}
	if(flag) return now;
		else return 0;
}

int main() {
//	freopen("tree.in", "r", stdin);
//	freopen("tree.out", "w", stdout);
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)
		scanf("%d", &s[i]);
	for(int i = 1; i < n; i++) {
		scanf("%d %d", &x, &y);
		add(y, x);
	}
	init_lg();
	init_dfs(1, 0);
	scanf("%d", &m);
	for(int i = 1; i <= m; i++) {
		scanf("%d %d", &x, &y);
		printf("%d\\n", work(x, y));
	} 
}