数学曲面(Mathematical Surfaces)

Posted 2021-08-10 大哥大嫂过年好啊

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数学曲面(Mathematical Surfaces)相关的知识，希望对你有一定的参考价值。

原文 https://catlikecoding.com/unity/tutorials/basics/mathematical-surfaces/

创建一个函数库。

使用委托和枚举

用网格显示2D函数

在3D空间定义表面

Unity 2020.3.6f1.

1. 函数库(Function Library)

1.1 库类(Library Class)

创建一个C#脚本 FunctionLibrary ，将其放到Scripts 文件夹。清空内容并声明一个 FunctionLibrary 类

using UnityEngine;

public class FunctionLibrary {}

这个类不是作为组件的，我们也不会创建一个对象来实例它。我们将其作为一个数学函数的集合，就像Unity的Mathf

在class前写下static关键字，将这个类变为静态类。

public static class FunctionLibrary {}

1.2 功能方法(Function Method)

我们的第一个功能是正弦波形。我们将为其创建一个方法，命名为Wave

public static class FunctionLibrary {

	void Wave () {}
}

默认情况下，方法都是实例方法，也就是说它们必须通过一个实例对象来调用。为了在类这个级别直接调用，我们用static关键字将其声明为静态函数。

static void Wave () {}

用public将其声明为共有的

public static void Wave () {}

这个函数将用来表示 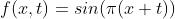$f(x,t) = sin(\\pi (x+t))$ 。这意味着它必须有一个返回值，并且是浮点型。所以讲void替换为为float

public static float Wave () {}

接着我们需要给函数添加两个参数。

public static float Wave (float x, float t) {}

现在我们将计算波形的代码放到里面，使用它的 x 和 t 参数

	public static float Wave (float x, float t) {
		Mathf.Sin(Mathf.PI * (x + t));
	}

最后是指定函数的返回值。我们通过直接返回计算的值来指定返回值。

	public static float Wave (float x, float t) {
		return Mathf.Sin(Mathf.PI * (x + t));
	}

现在可以在Graph.Update中使用这个函数，将position.x 和 time 作为参数。将它的返回值负值给点的Y坐标。

	void Update () {
		float time = Time.time;
		for (int i = 0; i < points.Length; i++) {
			Transform point = points[i];
			Vector3 position = point.localPosition;
			position.y = FunctionLibrary.Wave(position.x, time);
			point.localPosition = position;
		}
	}

1.3 隐式的使用类型(Implicitly using a Type)

我们将在FunctionLibrary 中使用很多Mathf 的函数，最好我们在写这些函数时能够不必写类名。我们可以在FunctionLibrary 文件的顶部添加一个using 声明，在UnityEngine.Mathf 类型前添加一个static关键字。

using UnityEngine;

using static UnityEngine.Mathf;

public static class FunctionLibrary { … }

现在我们可以在代码中省略Mathf.

	public static float Wave (float x, float z, float t) {
		return Sin(PI * (x + t));
	}

1.4 第二个函数(A Second Function)

让我们添加另一个函数。这次我们使用多个正弦来创建一个稍微复杂的函数。首先复制Wave函数并重命名为MultiWave

	public static float Wave (float x, float t) {
		return Sin(PI * (x + t));
	}

	public static float MultiWave (float x, float t) {
		return Sin(PI * (x + t));
	}

我们让然使用目前的正弦函数，但是会加一点东西。我们先将当前的返回值赋值给一个 y 变量，再将其返回。

	public static float MultiWave (float x, float t) {
		float y = Sin(PI * (x + t));
		return y;
	}

一个简单的增加正弦复杂性的方法是让其加一个双倍频率的正弦。也就是说，通过将正弦函数的参数乘以2，它的变化会快两倍。这时，我们也得到了了函数的返回值。正弦的形状保持不变，但是尺寸会减半。

		float y = Sin(PI * (x + t));
		y += Sin(2f * PI * (x + t)) / 2f;
		return y;

现在我们的数学函数是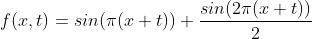 $f(x,t)=sin(\\pi (x+t))+\\frac{sin(2\\pi (x+t))}{2}$ 。由于正弦的正负极限是1 和 -1，新函数的最大和最小值应该是1.5 和 -1.5。为了保证在我们的-1 -- 1区间，我们需要将总值除以1.5

return y / 1.5f;

除法比乘法要耗时，所以通常会用乘法代替除法。

		y += 0.5f * Sin(2f * PI * (x + t));
		return y * (2f / 3f);

现在用这个函数替换掉Graph.Update的Wave函数

			position.y = FunctionLibrary.MultiWave(position.x, time);

Sum of two sine waves.

您可以说较小的正弦波现在跟随较大的正弦波。我们还可以使较小的波浪沿着较大的波浪滑动，例如将较大波浪的时间减半。结果将是一个函数，它不仅会随着时间的推移而滑动，还会改变其形状。现在模式需要四秒钟才能重复。

		float y = Sin(PI * (x + 0.5f * t));
		y += 0.5f * Sin(2f * PI * (x + t));

Morphing wave.

1.5 在编辑器中选择功能(Selecting Functions in the Editor)

接下来我们添加一些代码，以便可以控制Graph 使用哪个方法。我们添加一个滑动条，就像graph的分辨率一样(resolution)。因为我们有两个功能供选择，我们的区间是整型0 - 1。将其命名为 function。

	[SerializeField, Range(10, 100)]
	int resolution = 10;
	
	[SerializeField, Range(0, 1)]
	int function;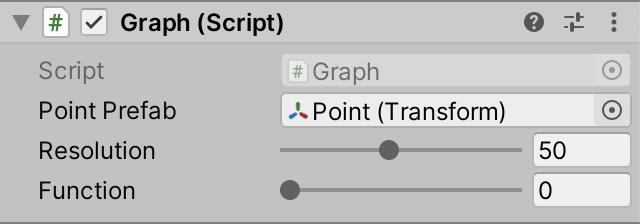

Function slider.

现在我们在Update的循环中判断function，如果是0则显示Wave。

	void Update () {
		float time = Time.time;
		for (int i = 0; i < points.Length; i++) {
			Transform point = points[i];
			Vector3 position = point.localPosition;
			if (function == 0) {
				position.y = FunctionLibrary.Wave(position.x, time);
			}
			point.localPosition = position;
		}
	}

如果不是0则显示MultWave

			if (function == 0) {
				position.y = FunctionLibrary.Wave(position.x, time);
			}
			else {
				position.y = FunctionLibrary.MultiWave(position.x, time);
			}

这样我们就可以通过graph的inspector控制功能了。

1.6 波纹功能(Ripple Function)

让我们为我们的库添加第三个函数，它会产生涟漪效果。我们通过使正弦波远离原点来创建它，而不是始终沿着同意方向。我们可以基于其到中心点的距离来实现它，也就是X的绝对值。我们以仅仅计算这个值作为开始，在一个新的FunctionLibrary.Ripple 函数中，使用Mathf.Abs

	public static float Ripple (float x, float t) {
		float d = Abs(x);
		return d;
	}

为了显示它，将Graph.function 的范围增加到2，并在Update中添加一个代码块。

	[SerializeField, Range(0, 2)]
	…

	void Update () {
		float time = Time.time;
		for (int i = 0; i < points.Length; i++) {
			Transform point = points[i];
			Vector3 position = point.localPosition;
			if (function == 0) {
				position.y = FunctionLibrary.Wave(position.x, time);
			}
			else if (function == 1) {
				position.y = FunctionLibrary.MultiWave(position.x, time);
			}
			else {
				position.y = FunctionLibrary.Ripple(position.x, time);
			}
			point.localPosition = position;
		}
	}

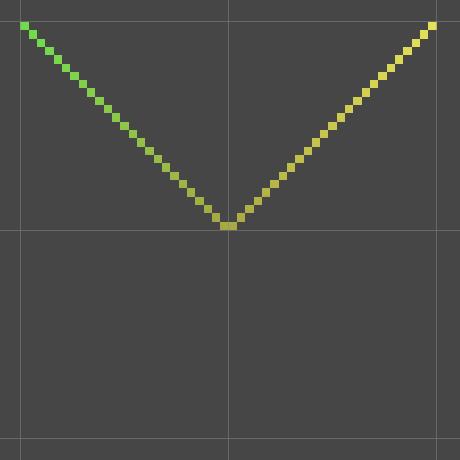
Absolute X.

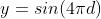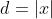回到FunctionLibrary.Ripple，我们使用距离作为正弦函数的输入，并将结果作为输出。我们使用 $y=sin(4\\pi d)$ 同时 d=|x| ，因此波纹会上下波动好几倍。

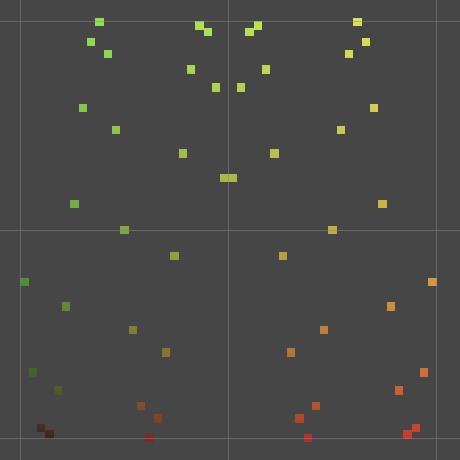
Sine of distance.

这个结果在视觉上难以解释，因为Y的变化太大了。我们可以通过降低振幅来改善它。但是波纹并没有一个固定的振幅，它会随着距离而减小。因此我们将函数改为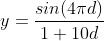 $y=\\frac{sin(4\\pi d)}{1+10d}$

		float y = Sin(4f * PI * d);
		return y / (1f + 10f * d);

完成的曲线应该是一个动态的波纹。为了使其向外波动，我们需要将正弦函数的参数减去时间。让我们使用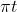 $\\pi t$ ，因此最后的函数是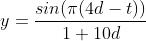 $y=\\frac{sin(\\pi (4d-t))}{1+10d}$

		float y = Sin(PI * (4f * d - t));
		return y / (1f + 10f * d);

Animated ripple.

2 管理函数 (Managing Methods)

一系列条件块适用于两三个函数，但在支持更多函数时变得笨拙。

2.1 委托(Delegates)

使用委托可以得到一个方法的引用。委托是一个特殊的类型，它定义了那种函数可以引用。我们的数学方法没有一个标准的委托类型，但是我们可以自己定义一个。

为创建一个委托，复制Wave函数，重命名为Function并将其代码块替换成分号。将static关键字替换为delegate我们就创建了一个委托。

public static class FunctionLibrary {
	
	public delegate float Function (float x, float t);
	
	…
}

现在我们可以引进一个GetFunction函数，它使用if-else返回一个给定索引的函数。

	public delegate float Function (float x, float t);
	
	public static Function GetFunction (int index) {
		if (index == 0) {
			return Wave;
		}
		else if (index == 1) {
			return MultiWave;
		}
		else {
			return Ripple;
		}
	}

接着，我们在Graph.Update的开始使用这个方法来获取一个函数的委托，基于function，并存储在一个变量里。

	void Update () {
		FunctionLibrary.Function f = FunctionLibrary.GetFunction(function);
		…
	}

然后在在循环中调用这个委托变量

		for (int i = 0; i < points.Length; i++) {
			Transform point = points[i];
			Vector3 position = point.localPosition;
			//if (function == 0) {
			//	position.y = FunctionLibrary.Wave(position.x, time);
			//}
			//else if (function == 1) {
			//	position.y = FunctionLibrary.MultiWave(position.x, time);
			//}
			//else {
			//	position.y = FunctionLibrary.Ripple(position.x, time);
			//}
			position.y = f(position.x, time);
			point.localPosition = position;
		}

2.2 一个委托数组(An Array of Delegates)

我们已经简化了一些Graph.Update，但是我们只是将if-esle代码移到了FunctionLibrary.GetFunction里。我们可以通过使用数组完全的拜托这些。首先在FunctionLibrary中添加一个静态的functions 数组。这个数组只在内部使用，所以不添加public。

	public delegate float Function (float x, float t);

	static Function[] functions;

	public static Function GetFunction (int index) { … }

将我们的方法按顺序填充数组

	static Function[] functions = { Wave, MultiWave, Ripple };

现在GetFunction函数可以简单的通过索引返回委托。

	public static Function GetFunction (int index) {
		return functions[index];
	}

2.3 枚举(Enumerations)

一个整型滑动条是有用的，但是并不像用0代表wave函数那样显而易见。如果我们有一个函数名的下拉框会更清晰。我们可以使用枚举来完成这些。

枚举可以通过定义一个enum 类型来实现。我们再次在FunctionLibrary 中做这些，这次命名为FunctionName。我们可以直接复制数组的元素。注意他们只是标签，不代表任何东西。

	public delegate float Function (float x, float t);

	public enum FunctionName { Wave, MultiWave, Ripple }

	static Function[] functions = { Wave, MultiWave, Ripple };

现在将GetFunction的索引参数替换为FunctionName的一个名字。这表示参数必须是一个有效的函数名。

	public static Function GetFunction (FunctionName name) {
		return functions[name];
	}

枚举可以被看作是语法糖。默认情况下，每个枚举的标签代表一个整型。第一个标签等于0，第二个是1，如此类推。所以我们可以使用他们的名字作为数组下标。然而编译器并不会自动的将枚举解释为整型，因此我们需要显式转换。

		return functions[(int)name];

最后一步是将Graph.function的类型改为FunctionLibrary.FunctionName 并且移除Range 属性。

	//[SerializeField, Range(0, 2)]
	[SerializeField]
	FunctionLibrary.FunctionName function;

Function dropdown list.

3 添加另一个维度(Adding Another Dimension)

目前为止我们的图形只包含一条线。我们将一维值映射到其他一维值，但如果把时间考虑在内其实是把二维值映射到一维值。所以我们已经将高维输入映射到一维值。就像我添加时间，我们可以添加额外的空间维度。

当前，我们使用X维度作为函数的空间输入。Y维度是用来显示输出。这就留下了Z作为第二个可以用作输入的空间维度。添加Z作为输入来升级我们的线到方格。

3.1 3维颜色(3D Colors)

既然Z不在是常量，更改我们的Point Surface 着色器，以便它也可以修改蓝色反射率部分

			surface.Albedo = saturate(input.worldPos * 0.5 + 0.5);

调整我们的Point URP 着色器，使Z被视为与X和Y一样。

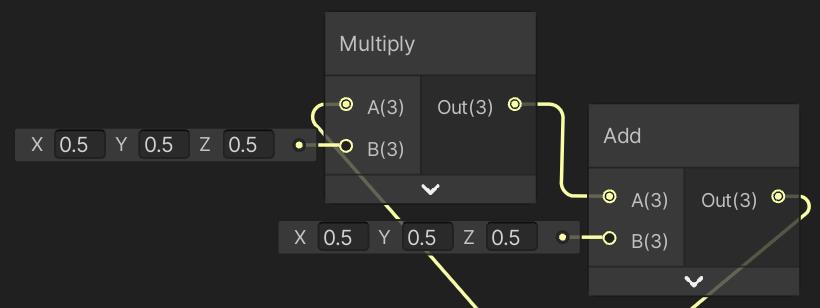
Adjusted Multiply and Add node inputs.

3.2 更新函数(Upgrading the Functions)

为了让我们的函数支持第二个非时间输入，在FunctionLibrary.Function 委托的x参数之后添加一个z参数。

	public delegate float Function (float x, float z, float t);

我们也需要在我们的三个函数中添加参数。

	public static float Wave (float x, float z, float t) { … }
	
	public static float MultiWave (float x, float z, float t) { … }
	
	public static float Ripple (float x, float z, float t) { … }

同时在Graph.Update.调用函数时添加position.z 作为参数。

			position.y = f(position.x, position.z, time);

3.3 创建点的网格(Creating a Grid of Points)

为了显示Z维度，我们需要将我们的线转成网格。我们可以通过创建多条线来实现，每条线沿着Z轴偏移一步。我们的Z将使用和X一样的区间，因此我们将创建我们当前点一样多的线。

		points = new Transform[resolution * resolution];

考虑到第二个维度我们必须调整循环。

首先，让我们明确的追踪X坐标。在for循环中，i变量的旁边声明一个x变量并使其自增长。

		points = new Transform[resolution * resolution];
		for (int i = 0, x = 0; i < points.Length; i++, x++) {
			…
		}

每次当一行结束时我们需要重设x为0。当x等于resolution时一行就结束了，所以我们可以在循环的顶部使用if块来实现。然后使用x替换i来计算x坐标。

		for (int i = 0, x = 0; i < points.Length; i++, x++) {
			if (x == resolution) {
				x = 0;
			}
			Transform point = points[i] = Instantiate(pointPrefab);
			position.x = (x + 0.5f) * step - 1f;
			…
		}

接下来，每一行都要沿着z维度偏移。我们可以通过给for循环增加一个z变量来实现。这个变量不可以每次迭代都递增。反而，只有当我们移动到下一行时，也就是在if块中，才增加。然后像X坐标一样设置Z坐标，使用z代替x。

		for (int i = 0, x = 0, z = 0; i < points.Length; i++, x++) {
			if (x == resolution) {
				x = 0;
				z += 1;
			}
			Transform point = points[i] = Instantiate(pointPrefab);
			position.x = (x + 0.5f) * step - 1f;
			position.z = (z + 0.5f) * step - 1f;
			…
		}

我们现在创建了一个点的网格，而不再是一条线。

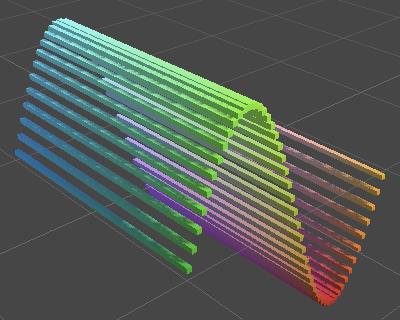
Graph grid.

3.4 更好的视觉效果(Better Visuals)

由于我们的图形现在是3D，从现在起我将用透视图观察它，在game窗口中。为了快速的选择一个好的摄像机位置，你可以在play模式的scene窗口中选择一个好的视角，退出play模式然后将game的摄像机匹配那个视角。你可以通过选择 GameObject / Align With View with Main Camera 来实现。

除此之外，我们可以稍微调整阴影质量。在使用默认渲染管线时，阴影可能已经看起来是可以接收的，但是他们被配置为可以看到很远而我们只是近距离观看我们的图形。

你可以在Quality project settings 为默认渲染管线选择质量级别

Quality levels.

我们可以通过在Shadows部分，减少Distance到10，设置Shadow Cascades为 No Cascades 来调整性能和阴影的精度。默认的设置会渲染阴影多次，这对我们来说太过了。

Shadow settings for default render pipeline.

URP不使用这些设置，它的阴影使用过我们URP资源的inspector配置的。它默认已经只渲染平行光阴影一次，但可以把Shadows / Max Distance 减到10。同时为了匹配默认渲染管线的Ultra质量，开启 Shadows / Soft Shadows 并将 Lighting 下的 Lighting / Main Light / Shadow Resolution 增加到4096。

Shadows settings for URP.

最后，你可能注意到了play模式时的撕裂。可以通过启动VSync (Game view only) 来防止这种情况，VSync 在Game窗口工具栏左侧的第二个下拉菜单。启动后，新帧的呈现和显示刷新的频率同步。这仅在没有scene窗口显示时才工作。可以通过quality settings的Other部分为独立程序设置Vsync。

VSnyc enabled for game window.

3.5 合并Z(Incorporating Z)

最简单的在Wave函数中使用Z的方式是使用X和Z的和替换X。这将创建一个对角波。

	public static float Wave (float x, float z, float t) {
		return Sin(PI * (x + z + t));
	}

最直接的改变MultiWave的方式是使每个波使用一个独立的维度。让最小的那个使用Z。

	public static float MultiWave (float x, float z, float t) {
		float y = Sin(PI * (x + 0.5f * t));
		y += 0.5f * Sin(2f * PI * (z + t));
		return y * (2f / 3f);
	}

Two waves in different dimensions.

我们还可以添加第三个波使其沿着XZ轴移动。让我们使用与Wave相同的波，除了将时间减慢四分之一。然后将结果除以2.5以使其在-1 -- 1 的区间内。

		float y = Sin(PI * (x + 0.5f * t));
		y += 0.5f * Sin(2f * PI * (z + t));
		y += Sin(PI * (x + z + 0.25f * t));
		return y * (1f / 2.5f);

注意，第一个波和第三个波会在固定间隔相互抵消。

Triple wave.

最后，为了使波纹在XZ平面的所有方向扩散，我们需要计算两个维度的距离。我们可以说会用勾股定理来计算，使用Mathf.Sqrt 方法。

	public static float Ripple (float x, float z, float t) {
		float d = Sqrt(x * x + z * z);
		float y = Sin(PI * (4f * d - t));
		return y / (1f + 10f * d);
	}

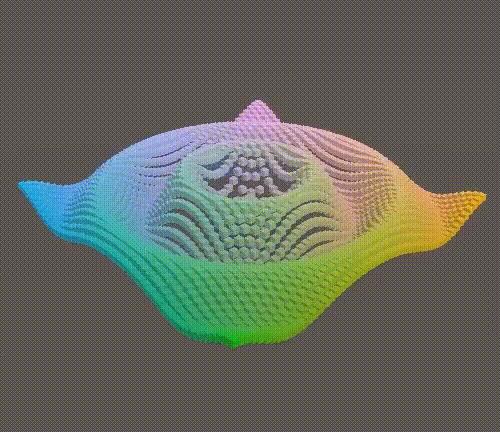
Ripple on XZ plane.

4 离开网格(Leaving the Grid)

通过使用X和Z来定义Y，我们可以创建定义各种各样表面的函数，但是它们总和XZ平面有关联。没有两个点在Y坐标不同时有同样的X和Z坐标。也就是说我们的曲面是有限的。它们的斜率不可能是垂直的并且它们不可能向后折叠。

4.1 三维函数(Three-Dimensional Functions)

如果我们的函数输出3D位置而不是1D值，我们可以用它们创建任意表面。比如，函数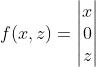 $f(x,z)=\\begin{vmatrix} x\\\\ 0\\\\ z \\end{vmatrix}$ 描述了XZ平面，而函数 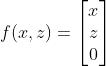$f(x,z)=\\begin{bmatrix} x\\\\ z\\\\ 0 \\end{bmatrix}$ 描述了XY平面。

因为函数的输入参数不在和最终的X和Z坐标一致，将它们命名为x和z就不在恰当了。它们被用来创建参数表面，通常被命名为 u 和 v。所以我们的函数像这样

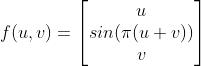
$f(u,v)=\\begin{bmatrix} u\\\\ sin(\\pi (u+v))\\\\ v \\end{bmatrix}$

调整我们的Function 委托以支持这个新的方式。需要做的修改仅仅是将float 替换为 Vector3，同时让我们修改参数名。

	public delegate Vector3 Function (float u, float v, float t);

我们还需要相应的修改我们的函数。我们直接用 U 和 V 替换 X 和 Z 。并非必须修改参数名--只需它们的类型与委托相匹配--但是让我们也这么做以保持一致。

先从Wave开始，在它的开始声明一个Vector3 变量，然后设置它的组件，然后返回它。

	public static Vector3 Wave (float u, float v, float t) {
		Vector3 p;
		p.x = u;
		p.y = Sin(PI * (u + v + t));
		p.z = v;
		return p;
	}

然后是MultiWave 和 Ripple

	public static Vector3 MultiWave (float u, float v, float t) {
		Vector3 p;
		p.x = u;
		p.y = Sin(PI * (u + 0.5f * t));
		p.y += 0.5f * Sin(2f * PI * (v + t));
		p.y += Sin(PI * (u + v + 0.25f * t));
		p.y *= 1f / 2.5f;
		p.z = v;
		return p;
	}

	public static Vector3 Ripple (float u, float v, float t) {
		float d = Sqrt(u * u + v * v);
		Vector3 p;
		p.x = u;
		p.y = Sin(PI * (4f * d - t));
		p.y /= 1f + 10f * d;
		p.z = v;
		return p;
	}

因为点的X和Z坐标不在是恒定的，我们也可以不在依赖于它们在Graph.Update 中的初始值。我们可以使用Awake中的循环来替换Update中的循环，除了我们现在可以直接用函数返回值赋值给点的位置。

	void Update () {
		FunctionLibrary.Function f = FunctionLibrary.GetFunction(function);
		float time = Time.time;
		float step = 2f / resolution;
		for (int i = 0, x = 0, z = 0; i < points.Length; i++, x++) {
			if (x == resolution) {
				x = 0;
				z += 1;
			}
			float u = (x + 0.5f) * step - 1f;
			float v = (z + 0.5f) * step - 1f;
			points[i].localPosition = f(u, v, time);
		}
	}

注意我们只需要在z改变时重新计算v。这需要我们在循环开始前设置它的初始值。

		float v = 0.5f * step - 1f;
		for (int i = 0, x = 0, z = 0; i < points.Length; i++, x++) {
			if (x == resolution) {
				x = 0;
				z += 1;
				v = (z + 0.5f) * step - 1f;
			}
			float u = (x + 0.5f) * step - 1f;
			//float v = (z + 0.5f) * step - 1f;
			points[i].localPosition = f(u, v, time);
		}

我们不必再Awake中初始化位置，所以我们可以让它简单一点。

	void Awake () {
		float step = 2f / resolution;
		var scale = Vector3.one * step;
		//var position = Vector3.zero;
		points = new Transform[resolution * resolution];
		for (int i = 0; i < points.Length; i++) {
			//if (x == resolution) {
			//	x = 0;
			//	z += 1;
			//}
			Transform point = Instantiate(pointPrefab);
			//position.x = (x + 0.5f) * step - 1f;
			//position.z = (z + 0.5f) * step - 1f;
			//point.localPosition = position;
			point.localScale = scale;
			point.SetParent(transform, false);
			points[i] = point;
		}
	}

4.2 创建一个球体(Creating a Sphere)

为了证明我们确实不在局限于每个(X,Z)坐标对一个点，让我们创建一个球体函数。为FunctionLibrary创建一个 Sphere 方法。同样也在FunctionName 枚举和 functions 数组为其创建入口。

	public enum FunctionName { Wave, MultiWave, Ripple, Sphere }

	static Function[] functions = { Wave, MultiWave, Ripple, Sphere };

	…

	public static Vector3 Sphere (float u, float v, float t) {
		Vector3 p;
		p.x = 0f;
		p.y = 0f;
		p.z = 0f;
		return p;
	}

创建球体的第一步是创建一个圆，平躺在XZ平面。我们使用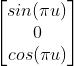 $\\begin{bmatrix} sin(\\pi u)\\\\ 0\\\\ cos(\\pi u) \\end{bmatrix}$

		p.x = Sin(PI * u);
		p.y = 0f;
		p.z = Cos(PI * u);

A circle.

我们现在有了多个圆，它们完美的重叠在一起。我们可以基于v将它们沿着Y挤出，我们得到一个没有盖子的圆柱体。

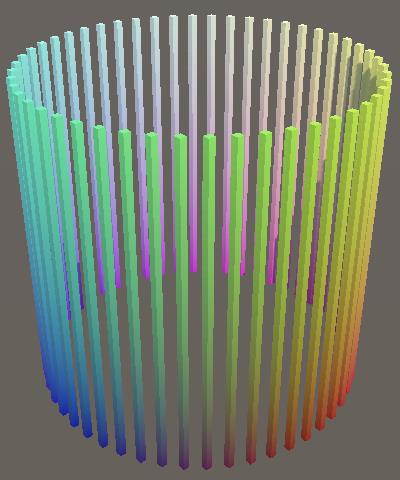
A cylinder.

我们可以调整圆柱的半径r，通过缩放X 和 Z。如果我们使用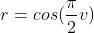 $r=cos(\\frac{\\pi}{2}v)$ 那么圆柱的顶部和底部会收缩到一个点。

		float r = Cos(0.5f * PI * v);
		Vector3 p;
		p.x = r * Sin(PI * u);
		p.y = v;
		p.z = r * Cos(PI * u);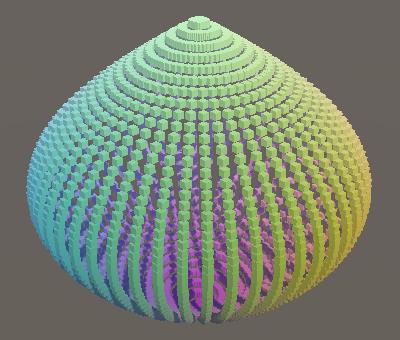

A cylinder with collapsing radius.

现在我们很接近一个球体了，但是圆柱半径的下降还不是圆形。因为圆形是由正弦和余弦组成，我们只使用了余弦。等式的另一部分是Y，目前仅仅是与v相等。为了完成圆我们需要使用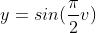 $y=sin(\\frac{\\pi}{2}v)$

p.y = Sin(PI * 0.5f * v);

A sphere.

结果是一个球体，用通常称为uv球体的模式创建。

4.3 扰乱球体(Perturbing the Sphere)

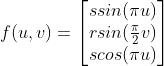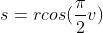让我们修改球体的表面让它更有趣。为此我们要修改我们的公式。我们使用 $f(u,v)=\\begin{bmatrix} s sin(\\pi u)\\\\ r sin(\\frac{\\pi}{2}v)\\\\ s cos(\\pi u) \\end{bmatrix}$ 同时 $s = r cos(\\frac{\\pi}{2}v)$ ，r 是半径。这可以时半径动起来。例如我们可以使用 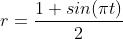$r = \\frac{1+sin(\\pi t)}{2}$ 使其基于时间缩放。

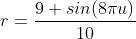
$r=\\frac{9+sin(8\\pi u)}{10}$

Scaling sphere.

我们不必使用一个统一的半径。我们可以基于u改变它，比如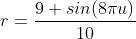 $r=\\frac{9+sin(8\\pi u)}{10}$

		float r = 0.9f + 0.1f * Sin(8f * PI * u);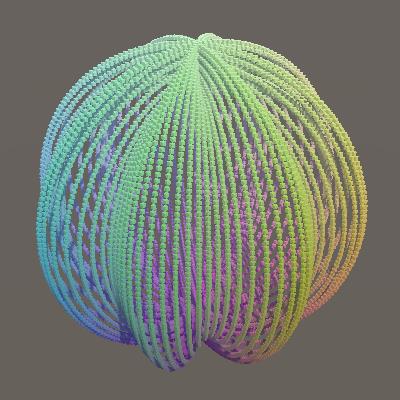

Sphere with vertical bands; resolution 100.

这使球体具有垂直带的外观。我们可以通过使用v代替u来切换到水平带。

		float r = 0.9f + 0.1f * Sin(8f * PI * v);

Sphere with horizontal bands.

两者同时使用给我们带来扭曲带。让我们也用时间使其旋转起来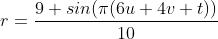， $r=\\frac{9+sin(\\pi (6u+4v+t))}{10}$

		float r = 0.9f + 0.1f * Sin(PI * (6f * u + 4f * v + t));

Rotating twisted sphere.

4.4 创建一个花环(Creating a Torus)

让我们给FunctionLibrary.添加一个花环表面。复制Sphere，重命名为Torus并将它的半径设为1。

	public enum FunctionName { Wave, MultiWave, Ripple, Sphere, Torus }

	static Function[] functions = { Wave, MultiWave, Ripple, Sphere, Torus };

	…

	public static Vector3 Torus (float u, float v, float t) {
		float r = 1f;
		float s = r * Cos(0.5f * PI * v);
		Vector3 p;
		p.x = s * Sin(PI * u);
		p.y = r * Sin(0.5f * PI * v);
		p.z = s * Cos(PI * u);
		return p;
	}

我们可以通过将其垂直的半圆相互拉开并将它们变成完整的圆来将我们的球体变形为环面。

		float s = 0.5f + r * Cos(0.5f * PI * v);

Sphere pulled apart.

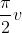
我们得到了半个花环，只有它环的外部。为了完成花环我们需要使用v来描述整个圆环。为此我们可以在s 和 y 中使用 $\\pi v$ 替换 $\\frac{\\pi}{2}v$

		float s = 0.5f + r * Cos(PI * v);
		Vector3 p;
		p.x = s * Sin(PI * u);
		p.y = r * Sin(PI * v);
		p.z = s * Cos(PI * u);

A self-intersecting spindle torus.

因为我们已经将球体分开了半个单位，这会产生一个自相交的形状，称为纺锤体环面。如果我们将它拉开一个单位，我们就会得到一个不自相交但也没有孔的环面，这被称为角环面。因此，我们将球体拉开的距离会影响环面的形状。具体来说，它定义了圆环的主半径。另一个半径是小半径，决定了环的厚度。让我们定义主半径为 r1 并将另一个重命名为 r2 因此。使用0.75为主半径，0.25位小半径，使点在-1 -- 1区间内。

		//float r = 1f;
		float r1 = 0.75f;
		float r2 = 0.25f;
		float s = r1 + r2 * Cos(PI * v);
		Vector3 p;
		p.x = s * Sin(PI * u);
		p.y = r2 * Sin(PI * v);
		p.z = s * Cos(PI * u);

A ring torus.

现在我们可以使用两个半径来制作有趣的圆环。例如我们可以使用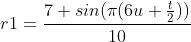 $r1=\\frac{7+sin(\\pi (6u+\\frac{t}{2}))}{10}$ 来将它转换成旋转的星星，同时用 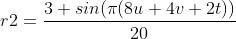$r2=\\frac{3+sin(\\pi(8u+4v+2t))}{20}$ 来扭曲环。

		float r1 = 0.7f + 0.1f * Sin(PI * (6f * u + 0.5f * t));
		float r2 = 0.15f + 0.05f * Sin(PI * (8f * u + 4f * v + 2f * t));

Twisting torus.

以上是关于数学曲面(Mathematical Surfaces)的主要内容，如果未能解决你的问题，请参考以下文章

数学曲面(Mathematical Surfaces)

CodeForces - 1584A Mathematical Addition数学计算

[中英双语] 数学缩写列表 (List of mathematical abbreviations)

HDU 1017 A Mathematical Curiosity (数学)