复盘动态规划（线性）7.10

Posted 2021-08-10 karshey

从题目中学习。

A - 数塔

来源：HDU 2084

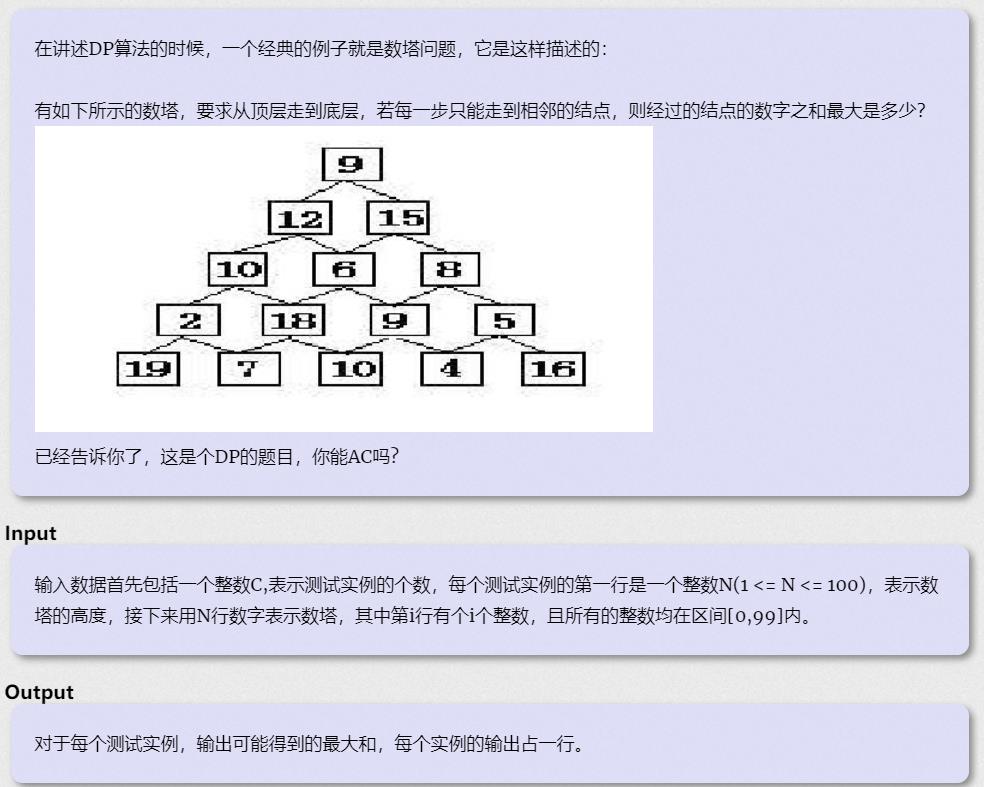
输入：

1
5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

输出：

30

从下往上加取最大值即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105;
int a[N][N];

int main()
{
	int t;cin>>t;
	while(t--)
	{
		int n;cin>>n;
		memset(a,0,sizeof(a));
		
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=i;j++)
			{
				cin>>a[i][j];
			}
		}
		
//		//输出数塔 
//		for(int i=1;i<=n;i++)
//		{
//			for(int j=1;j<=i;j++)
//			{
//				cout<<a[i][j]<<" ";
//			}
//			cout<<endl;
//		}
//		//
		for(int i=n;i>1;i--)
		{
			for(int j=1;j<i;j++)
			{
				a[i-1][j]+=max(a[i][j],a[i][j+1]);
			}
		}
		cout<<a[1][1]<<endl;
	}
	return 0;
}

B - Super Jumping! Jumping! Jumping!

来源：HDU 1087


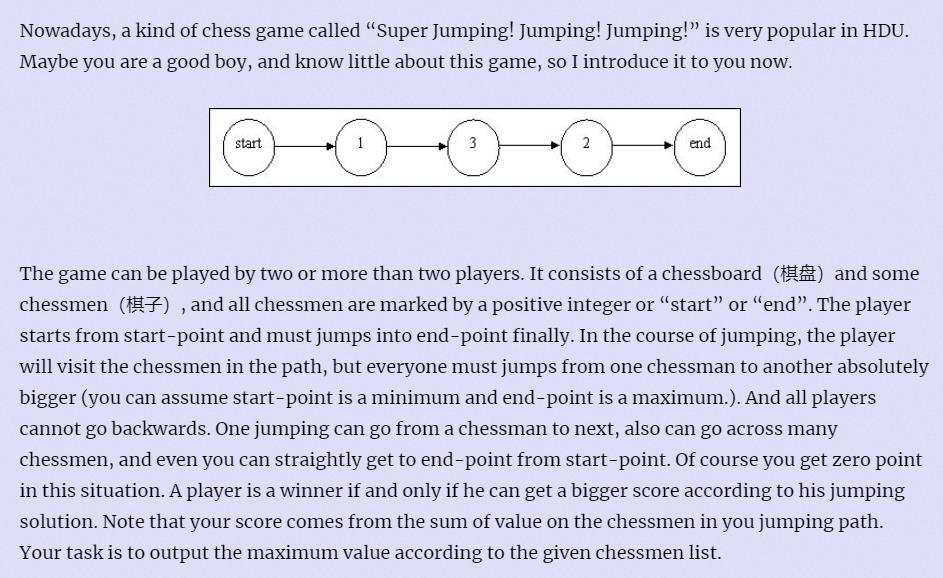
输入：

3 1 3 2
4 1 2 3 4
4 3 3 2 1
0

输出：

4
10
3

题意：
从start开始，到end结束，经过的每一个数字都只能严格从小到大，不可返回，求经过之和的最大值。
方程：dp[i]是第i位置的最大值。
dp[i]=max(dp[i],dp[j]+a[j]);直接跳到i，或者通过j更新i（从j跳到i）。
求最大值要全初始化为0.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
int a[N];
int main()
{
	int n;
	while(cin>>n&&n)
	{
		memset(a,0,sizeof(a));
		for(int i=0;i<n;i++) 
		{
			cin>>a[i];			
		}
		
		int dp[N];
		memset(dp,0,sizeof(dp));
		dp[0]=a[0];		
		
		for(int i=1;i<n;i++)
		{
			dp[i]=a[i];
			for(int j=0;j<i;j++)
			{
				if(a[j]<a[i])
				{
					dp[i]=max(dp[i],dp[j]+a[i]);
				}
			}
			dp[i]=max(dp[i],a[i]);
		}
		int ans=-1;
		for(int i=0;i<n;i++)
		{
			ans=max(ans,dp[i]);
		}
		cout<<ans<<endl;
	}
	return 0;
}

C - 免费馅饼

来源：HDU 1176

输入：

6
5 1
4 1
6 1
7 2
7 2
8 3
0

输出：

4

可以转化为类似数塔的模型，如：

          5
        4 5 6 
      3 4 5 6 7 
    2 3 4 5 6 7 8   
  1 2 3 4 5 6 7 8 9 
0 1 2 3 4 5 6 7 8 9 10

然后从下往上叠加：

a[i][j]+=max(a[i+1][j-1],max(a[i+1][j],a[i+1][j+1]));

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int a[N][15];

int main()
{
	int n;
	while(scanf("%d",&n)&&n)
	{
		memset(a,0,sizeof(a));
		int m=0;
		while(n--)
		{
			int x,t;scanf("%d%d",&x,&t);
			a[t][x]++;
			if(t>m) m=t;
		}
		
		//第一个是时间，第二个是位置 
		for(int i=m-1;i>=0;i--)
		{
			for(int j=0;j<=10;j++)
			{
				a[i][j]+=max(a[i+1][j],max(a[i+1][j+1],a[i+1][j-1]));
			}
		}
		
		cout<<a[0][5]<<endl;				
	}
	return 0;
}

D - Common Subsequence

来源：HDU 1159

输入：

abcfbc abfcab
programming contest 
abcd mnp

输出：

4
2
0

注意：dp[i][0],dp[0][j]都是0.
dp[i][j]代表a的前i个和b的前j个中的最大子序列。
如：abd acd中dp[1][1]即a a 所以为1.

方程：
如果比较的字符相同，dp[i][j]=dp[i-1][j-1]+1;
如果不同，dp[i][j]=max(dp[i-1][j],dp[i][j-1]);之前的最大的。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
int dp[N][N];
int main()
{
	string a,b;
	while(cin>>a>>b)
	{
		int len1=a.size(),len2=b.size();
		memset(dp,0,sizeof(dp));
		dp[0][0]=0;
		for(int i=0;i<=len1;i++)
		{
			for(int j=0;j<=len2;j++)
			{
				if(i==0||j==0) {dp[i][j]=0;continue;
				}
				
				if(a[i-1]==b[j-1]) dp[i][j]=dp[i-1][j-1]+1;
				else dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
			}
		}
		cout<<dp[len1][len2]<<endl;
	}
	return 0;
}

E - 搬寝室

来源：HDU 1421

输入：

2 1
1 3

输出：

4

注：数据量是n=2000，n^2 为1e6，1000ms（1e7）可以过。相当于这个数据量是在暗示我们开二维数组和双重循环。

dp方程：dp[i][j]代表拿了i个东西，j对的最小疲劳值。

dp[i][j]=min(dp[i-1][j],dp[i-2][j-1]+(a[i]-a[i-1])*(a[i]-a[i-1]));
//第一个是没拿，所以状态和上一个是一样的；
//第二个是拿了，拿的是i和i-1，要加上i-2的状态.

范围：i从2–n，因为方程中有i-2；j是1-k，题中2<=2*k,故j从1开始。
因为求最小值，所以dp[i][j]要初始化为INF，dp[i][0]即一对都没有拿初始化为0.

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2005;const ll inf=0x3f3f3f3f;
int a[N];
int dp[N][N];
int main()
{
	int n,k;
	while(cin>>n>>k)
	{
		for(int i=1;i<=n;i++)
		{
			cin>>a[i];
		}
		a[0]=0;
		sort(a+1,a+n+1);
		
		for(int i=0;i<=n;i++)
		{
			for(int j=1;j<=k;j++)
			{
				dp[i][j]=inf;
			}
		}
		for(int i=0;i<=n;i++)
		{
			dp[i][0]=0;
		}
		for(int i=2;i<=n;i++)
		{
			for(int j=1;j<=k;j++)
			{
				dp[i][j]=min(dp[i-2][j-1]+(a[i-1]-a[i])*(a[i-1]-a[i]),dp[i-1][j]);
			}
		}
		cout<<dp[n][k]<<endl;
	}
	
	return 0;
}