[树形dp] aw3760. 最大剩余油量(树的直径+树形dp+aw周赛007_3)

Posted 2021-08-09 Ypuyu

文章目录

• • 1. 题目来源
  • 2. 题目解析

1. 题目来源

链接：3760. 最大剩余油量

2. 题目解析

树的直径，两遍 dfs 或者树形 dp，或者。

树形结构，两点间的边为无向边，点的权值为正，边的权值为负。本题相当于求树中一条边权和最大的路径，就是求树的直径。

不太熟这个知识点，可以两遍 dfs，也可以直接使用树形 dp。

---

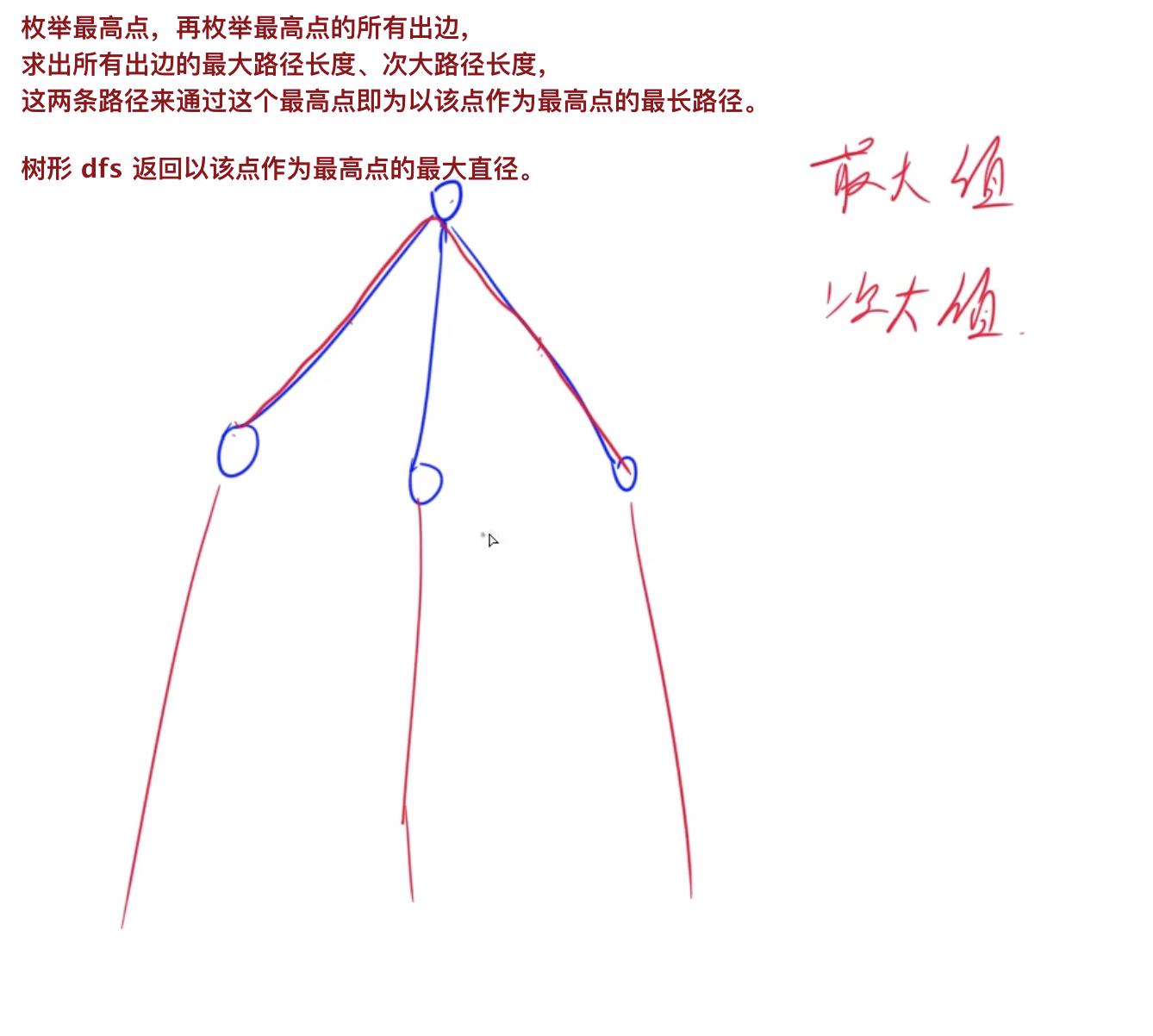
树形 dp 思路：

• 枚举路径中，树的最高点。
• 整个树的直径中，经过这个最高点，一定是由这个点的两个出边经过，无向边，方向无所谓。
• 树形 dfs 返回以该点作为最高点的最长路径。
• 枚举所有点，都作为最高点，全局维护答案 res 最长路径即可。
• 由于本树是连通的，从任一点开始枚举即可，dfs 会以出边将所有点作为最高点枚举到它的最长路径。
• 无向树，记录上一个点，避免重复访问。

笔记：

最长路径的话，使用虚拟源点+spfa 求最长路，按理说是正确的。但实际操作会出错，因为可能出现正环，spfa 无法处理正环问题。使用 dijkstra 可能是对的，但时间会多个 $O(logn)$，容易超时。

---

时间复杂度：$O(n)$

空间复杂度：$O(n)$

---

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 3e5+5, M = N * 2;

int n;
int h[N], e[M], w[M], ne[M], idx;
int cost[N];
LL res;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

LL dfs(int u, int father) {
    LL d1 = 0, d2 = 0;              // 最大值、次大值，若只有一条边向下走的情况下，边权为 0 即可
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        LL d = dfs(j, u);           // 返回出边作为最高点向下走的最大剩余油量，即向下的最大长度
        if (d < w[i]) continue;     // 如果走不上去的话，油量不足
        
        // 更新最大值、次大值
        d -= w[i];                  // 向上走的话，需要减去该边上的权值，此时 d 就是到达最高点 u 的最大剩余油量
        if (d >= d1) d2 = d1, d1 = d;  // 维护各个出边点到最高点的最大剩余油量，选择最大值、次大值
        else if (d > d2) d2 = d;
    }
    
    res = max(res, d1 + d2 + cost[u]);
    
    return d1 + cost[u];
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i ++ )  cin >> cost[i];
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ ) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }
    
    res = max(res, dfs(1, -1));
    cout << res << endl;
    
    return 0;
}