算法入门双指针（中等 - 第一题）LeetCode 3

Posted 2021-08-09 英雄哪里出来

🙉饭不食，水不饮，题必须刷🙉
还不会C语言，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？上简单题！ 🧡《C语言入门100例》🧡
LeetCode 太简单？大神盘他！ 🌌《夜深人静写算法》🌌

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识

一、题目

1、题目描述

  给定一个长度为 $n(1\le n\le 10^7)$ 的字符串 $s$，求一个最长的满足所有字符不重复的子串的长度。
  样例："$abcabcbbg$"，输出 $3$

2、基础框架

• c++ 版本给出的基础框架代码如下：

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
    }
};

• 其中 string是 C++ 的 STL 中的模板类，可以用来做字符串的各种操作；
  

3、原题链接

LeetCode 3. 无重复字符的最长子串

二、解题报告

1、思路分析

• 我们考虑一个子串以 $s_i$ 为左端点，$s_j$ 为右端点，且 $s[i:j-1]$ 中不存在重复字符，$s[i:j]$ 中存在重复字符（换言之，$s_j$ 和 $s[i:j-1]$ 中某个字符相同）。如图所示：
  
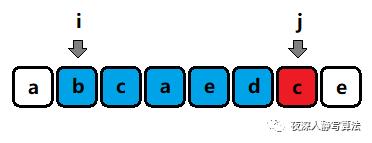
• 那么我们没必要再去检测 $s[i:j+1]$，$s[i:j+2]$，$s[i:n-1]$ 这几个字符串的合法性，因为当前情况 $s[i:j]$ 是非法的，而这些字符串是完全包含 $s[i:j]$ 的，所以它们必然也是不合法的。
• 那么我们可以把枚举的左端点自增，即： $i=i+1$，这时，按照朴素算法的实现，右端点需要重置，即 $j=i$，实际上这里的右端点可以不动。
• 可以这么考虑，由于 $s_j$ 这个字符和 $s[i:j-1]$ 中的字符产生了重复，假设这个重复的字符的下标为 $k$，那么 $i$ 必须满足 $i>k$，换言之， $i$ 可以一直自增，直到 $i=k+1$，如图所示：
  
• 这个问题是 双指针 问题的原题，详细的算法可以参考：夜深人静写算法（二十八）- 尺取法。

2、时间复杂度

• 两个指针都只会递增各一次，所以时间复杂度为 $O(n)$。

3、代码详解

class Solution {
    int hash[257];

public:
    int lengthOfLongestSubstring(string s) {
        memset(hash, 0, sizeof(hash));
        int maxLen = 0;
        int i = 0, j = -1;             // (1)
        int len = s.length();          // (2)
        while(j++ < len - 1) {
            ++hash[ s[j] ];            // (3)
            while(hash[ s[j] ] > 1) {  // (4)
                --hash[ s[i] ];        // (5)
                ++i;
            }
            if(j - i + 1 > maxLen) {   // (6)
                maxLen = j - i + 1;
            }
        }
        return maxLen;
    }
};

• $(1)$ 代表一开始是空串；
• $(2)$ 之所以要这么做，是因为s.length()是无符号整型，当 j == -1的情况为无符号整型的最大值，永远都无法进入下面的while(j++ < len - 1)这个循环；
• $(3)$ 尝试向右移动 右指针；
• $(4)$ 合法性判定：所有字符个数不超过1；
• $(5)$ 尝试向右移动 左指针；
• $(6)$ 更新最大合法长度；

---

三、本题小知识

无符号整型在进行判断的时候，如果赋值为 -1，就有可能导致变成整数最大值导致逻辑错误；

---