数字出现次数问题刷题篇——2

Posted 2021-08-08 林慢慢i

文章目录

• • 前言：
  • • 刷题前先提一下类似Leetcode和牛客网这类在线OJ的两种类型：接口型和IO型。
  • 正文：
  • • 1.只出现一次的数字
    • • • 思路实现：
    • 2.数组中数字出现的次数
    • • 2.1 找出两个只出现一次的数（其余数字均出现两次）
      • • 思路实现：
      • 2.2 找出一个只出现一次的数（其余数字均出现三次）
      • • 思路实现：
    • 3.消失的数字
    • • • 思路二实现(0~n计算等差数列和-数组中所有值相加)
        • 思路三实现(异或)

前言：

刷题前先提一下类似Leetcode和牛客网这类在线OJ的两种类型：接口型和IO型。

接口型：测试用例和结果一般是通过参数接口函数的参数和返回值交互的。IO型：测试用例通过IO输入来的，结果通过IO输出给的，需要自己写头文件、main函数，自己写输入获取测试用例。这两种类型对于OJ本质都是一样的，都是通过网络协议传送到网站的后台服务器，后台服务器会去运行所写的程序，通过测试用例检测正确性（批评下牛客网，程序出错不报测试用例给你，Leetcode就会报所有测试用例）。

正文：

1.只出现一次的数字

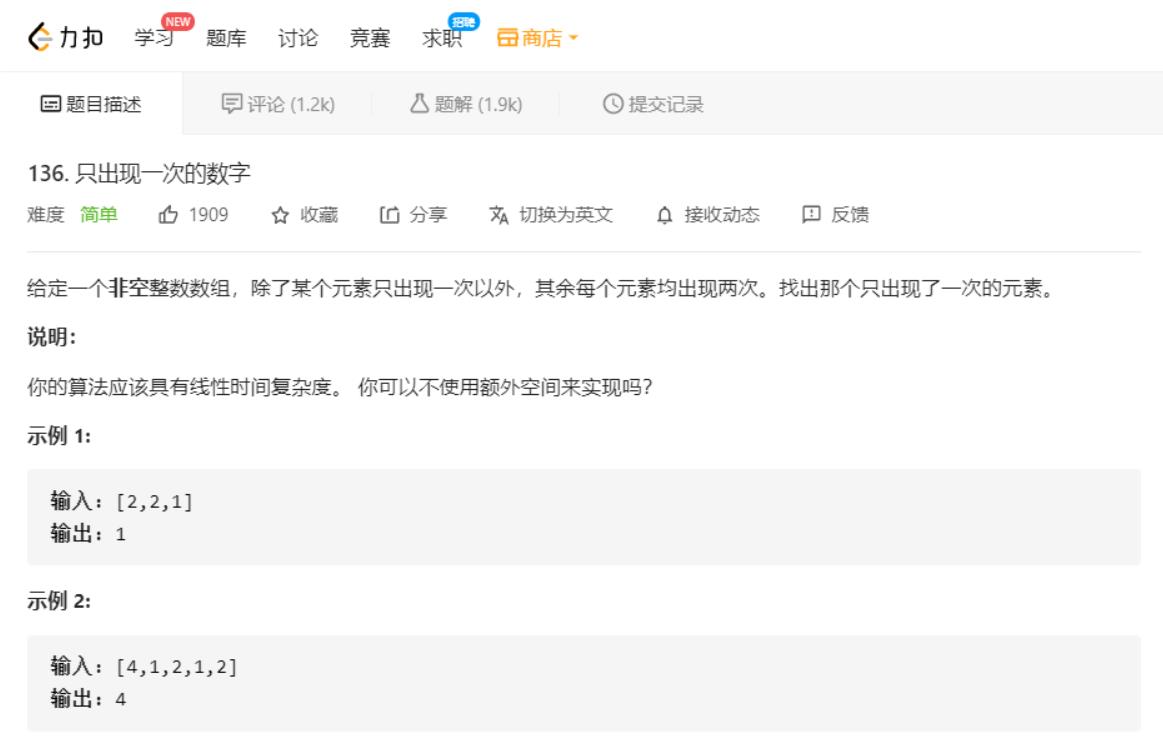
思路：

直接对数组所有元素进行异或，出现两次的数都会被抵消，最终结果就是只出现一次的数。

思路实现：

int singleNumber(int* nums, int numsSize){
    int ans = nums[0];
    for (int i = 1; i < numsSize; ++i) {
        ans ^= nums[i];
    }
    return ans;
}

2.数组中数字出现的次数

2.1 找出两个只出现一次的数（其余数字均出现两次）

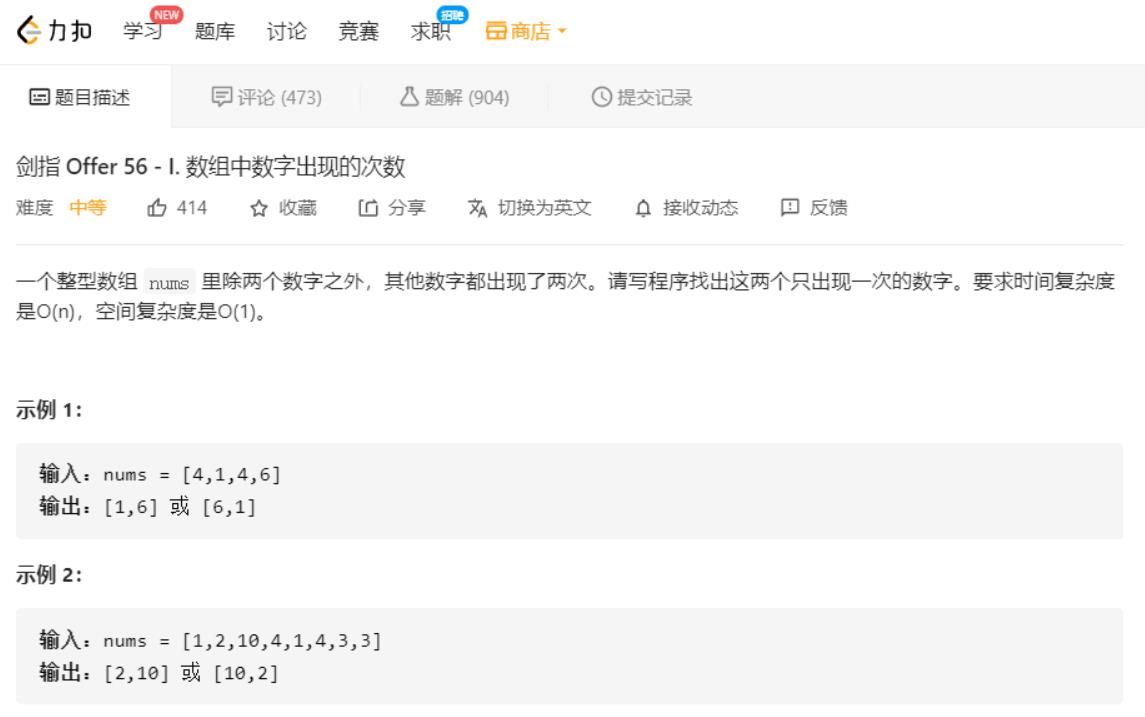
分析：

考虑异或操作的性质：对于两个操作数的每一位，相同结果为 00，不同结果为 11。那么在计算过程中，成对出现的数字的所有位会两两抵消为 00，最终得到的结果就是那个出现了一次的数字。

那么这一方法如何扩展到找出两个出现一次的数字呢？

如果我们可以把所有数字分成两组，使得：

两个只出现一次的数字在不同的组中；

相同的数字会被分到相同的组中。

那么对两个组分别进行异或操作，即可得到答案的两个数字。

思路（分组异或）：

第一步：引入ret=0，将数组中所有数都跟ret异或一下，假设出现一次的两个数是x和y，ret就是x^y

第二步：找ret里面随便一个为1的位（假设这位是第n位），说明x和y在第n位有一个为0且另一个为1

第三步：分组，把原数组中的数，第n位为1的分成一组，第n位为0的分成一组（这操作很秒！这样分刚好出现两次的数也必然被分到同一组）

第四步：分别对分好的两组各自进行组内所有数字的异或，即可分别得出数字

思路实现：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* singleNumbers(int* nums, int numsSize, int* returnSize){
    int ret = 0;
    for(int i=0;i<numsSize;++i)
    {
        ret^=nums[i];
    }
    //寻找ret里面一个为1的位j
    int j=0;
    for(;j<32;++j)
    {
        if(ret>>j&1)
        break;
    }
    //分组，异或
    int x=0,y=0;
    for(int k=0;k<numsSize;++k)
    {
        if(nums[k]>>j&1)
        {
            x^=nums[k];
        }
        else
        {
            y^=nums[k];
        }
    }
    int *arr=(int*)malloc(sizeof(int)*2);
    arr[0]=x;
    arr[1]=y;
    *returnSize=2;
    return arr;
}

2.2 找出一个只出现一次的数（其余数字均出现三次）

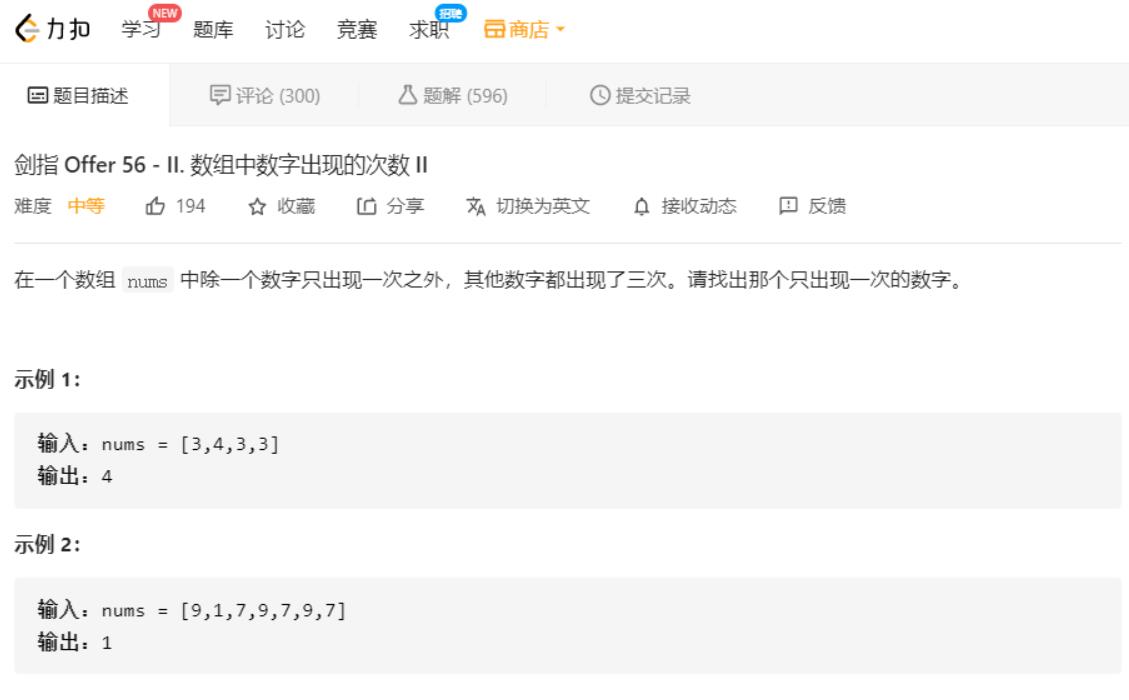
思路：

第一步：统计出数组中所有的数，第0位合计有多少个1，第1位合计有多少个1…第31位合计有多少个1。

第二步：0-31位统计出的1的个数%3，找出余数为1的那些位，这些位的组合就是出现一次的这个数。

从二进制的角度来看，int 类型占 32 个 bit 位，并且每个位，只可能是 1 或 0。
那么从 二进制 角度来看相同的数，二进制的 bit 位也是一样的，如：

7 : 0B0111
7 : 0B0111
7 : 0B0111
^^^
|||
出现数 333 // 从上向下，可以发现[3个7]每位都出次了 3 次

那这样时再增加一个数。
7 : 0B0111
7 : 0B0111
7 : 0B0111
4 : 0B0100
^^^
|||
出现数 433 // 从上向下，只有第 3位bit 出现了 4次
%%%
333 // 接下来，把现各个位出现的次数，按 3取余
‖‖‖
100 // 取余结果

从二进制的角度来看 100 也就对应的 10进制的 4
再来看一个例子：

7 : 0B0111
7 : 0B0111
7 : 0B0111
5 : 0B0101
4 : 0B0100
5 : 0B0101
5 : 0B0101
^^^
|||
出现数 736
%%%
333
‖‖‖
100 // 取余结果

该算法的逻辑，也就是通过统计所有数，每个 bit位 出现的 次数。
再把每个位的 次数 % 3，也就算出，只出现 1次数 的bit位。
最后再各个 bit 位拼接起来，就得到了只出现 1次 的数

思路实现：

int singleNumber(int* nums, int numsSize){
    int i;
    int ret = 0;
    for (i = 0; i < 32; i++) {
        int tmp = 0;
        int j;
        for (j = 0; j < numsSize; j++) {
            tmp += (nums[j] >> i) & 1;
        }

        if ((tmp % 3) != 0) {
            ret += 1 << i;
        }
    }

    return ret;
}

3.消失的数字

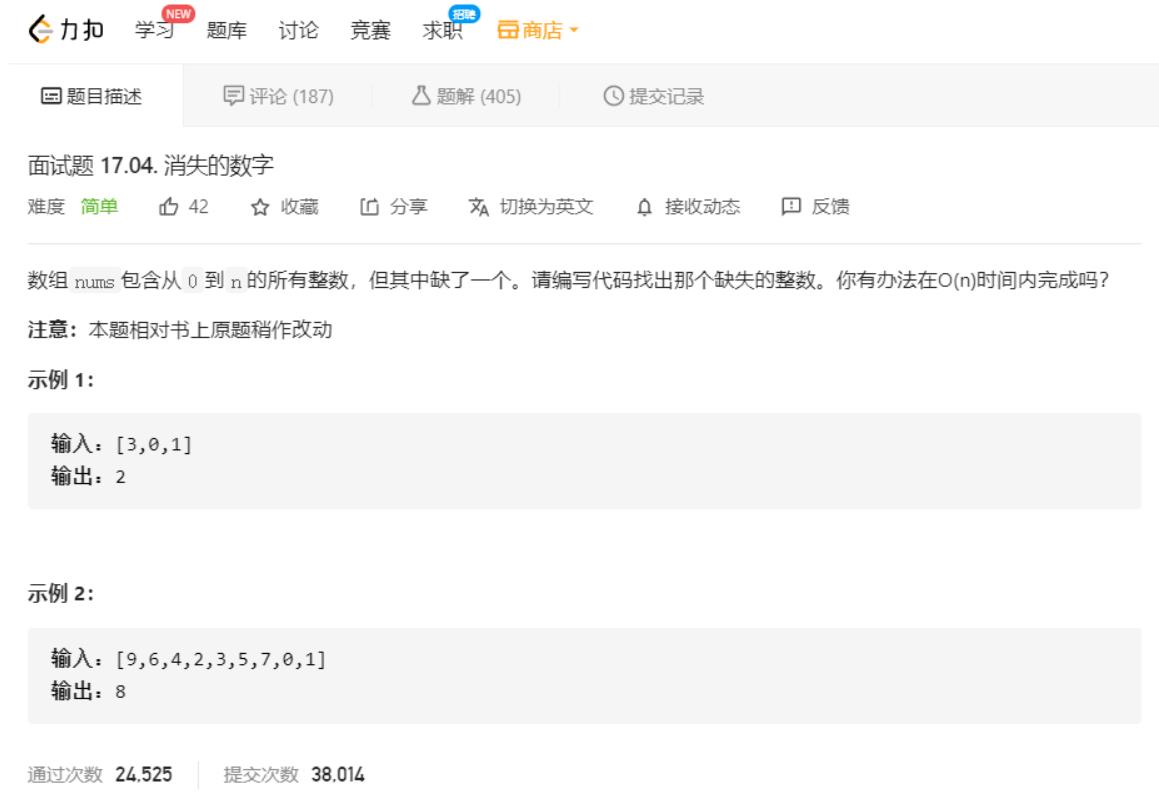
思路一（不合要求，抛弃）：

冒泡排序或qsort快排，但是由于存在时间复杂度的限制，放弃冒泡排序和qsort快排的方法。

思路二：

0~n计算等差数列和-数组中所有值相加。

思路三：

异或，把0~n的数字和数组中所有值进行一次异或，结果就是缺失的数字。（挺好理解的，一个数字出现两次，相互进行异或就变成0了，最终异或结果就只能是那个缺失的数字）

思路二实现(0~n计算等差数列和-数组中所有值相加)

int missingNumber(int* nums, int numsSize){
    int n=numsSize+1;
    int ret1=0;
    //0~n之间所有数累加
    for(int i=0;i<n;++i)
    {
        ret1+=i;
    }
    int ret2=0;
    //数组中所有数求和
    for(int j=0;j<numsSize;++j)
    {
        ret2+=nums[j];
    }
    return ret1-ret2;
}

思路三实现(异或)

int missingNumber(int* nums, int numsSize){
    int x=0;
    for(int i=0;i<numsSize+1;++i)
    {
        x^=i;
    }
    for(int j=0;j<numsSize;++j)
    {
        x^=nums[j];
    }
    return x;
}

如果内容对你有帮助的话，记得给我三连（点赞、收藏、关注）——做个手有余香的人。