C++二叉搜索树（BST）

Posted 2021-08-08 桃陉

一.基本介绍

特征：

二叉搜索树，也被称为二叉查找树、有序二叉树或者排序二叉树。
$\bullet$ 一般来说输入的第一个数作为根结点，当继续输入数时，小于根结点的放在根结点左边，大于根结点的放在根结点右边。
$\bullet$ 不只是根结点，每个子节点也符合左小右大的规律。
$\bullet$ 如下图所示，输入数据8、3、10、1、6、14、4、7、13，得到下面的二叉搜索树。

二叉查找树插入时间复杂度较低，为O(logn)，查找时间复杂度最坏为O(n)。

---

下面我们来介绍BST的构成成分：

$\bullet$ 首先我们需要实现两个类：一个是BSTNode类（节点类）、一个为BST类（二叉查找树类）。

$\bullet$ BSTNode类含有节点值 it 、左节点指针 lc、右节点指针 rc等私有变量，取值修改值、取节点修改节点、判断节点是否为叶子结点等公有函数。

$\bullet$ BST类含有根节点 root、节点个数 nodecount等私有变量，清空BST、插值、删除最小值、找到最小值、删除指定值、查找指定值、打印BST等函数。

$\bullet$ 需要注意的是我们采用了泛型编程来实现BST，这样在实际应用中应用更广。

---

在主函数中我们还实现了求和、找出小于指定值的数、找出位于两数之间的数等操作函数。具体实现过程见下面的代码。

二.代码实现

分为三个文件：

BSTNode.h:

#ifndef _BSTNODE_H_
#define _BSTNODE_H_
#include<iostream>
using namespace std;

/*
    采用泛型编程实现BST节点类，方便使用
*/
template<typename E> class BSTNode
 {
    private:
        E it;  //value
        BSTNode *lc;  //left node
        BSTNode *rc;  //right node
    public:
        //构造函数
        BSTNode() {lc=rc=NULL;}
        BSTNode(E e,BSTNode *l=NULL,BSTNode<E> *r=NULL){this->it=e;this->lc=l;this->rc=r;}
        //析构函数
        ~BSTNode(){}

        //取值
        E& element() {return it;}
        //修改值
        void setElement(const E& e) {it=e;}

        //取出左\\右结点
        inline BSTNode* left() const {return lc;}
        inline BSTNode* right() const {return rc;}
        //修改左右结点
        void setleft(BSTNode<E> *b) {lc=b;}
        void setright(BSTNode<E> *b) {rc=b;}

        //判断是否为叶结点
        bool isLeaf() {return (lc==NULL)&&(rc==NULL);}
};
#endif

BST.h：

#include<iostream>
#include<cstdlib>
#include"BSTNode.h"
using namespace std;
template<typename E>
class BST
{
    private:
        //根结点
        BSTNode<E>* root;
        int nodecount; //结点个数

        //清空BST树操作
        void clearhelp(BSTNode<E>* root)
        {
            if(root==NULL) return ;
            clearhelp(root->left());
            clearhelp(root->right());
            delete root;
        }

        //插入e到合适的位置
        BSTNode<E>* inserthelp(BSTNode<E>* root,const E&e)
        {
            if(root==NULL) return new BSTNode<E>(e,NULL,NULL);
            if(e<root->element())  root->setleft(inserthelp(root->left(),e));
            else root->setright(inserthelp(root->right(),e));
            return root;
        }

        //删除最小值，并将其他数排好序
        BSTNode<E>* deletemin(BSTNode<E>* rt)
        {
            if(rt->left()==NULL) return rt->right();
            else {
                rt->setleft(deletemin(rt->left()));
                return rt;
            }
        }

        //获得最小值
        BSTNode<E>* getmin(BSTNode<E>* rt)
        {
            if(rt->left()==NULL) return rt;
            else return getmin(rt->left());
        }

        //删除指定值
        BSTNode<E>* removehelp(BSTNode<E>* rt,const E& e)
        {
            if(rt==NULL) return NULL;
            else if(e<rt->element()) rt->setleft(removehelp(rt->left(),e));
            else if(e>rt->element()) rt->setright(removehelp(rt->right(),e));
            else 
            {
                BSTNode<E>* temp=rt;
                if(rt->left()==NULL)
                {
                    rt=rt->right();
                    delete temp;
                }else if(rt->right()==NULL)
                {
                    rt=rt->left();
                    delete temp;
                } else 
                {
                    BSTNode<E>* temp=getmin(rt->right());
                    rt->setElement(temp->element());
                    rt->setright(deletemin(rt->right()));
                    delete temp;
                }
            }
            return rt;
        }

        //寻找指定值
        E findhelp(BSTNode<E>* root,const E&e) const
        {
            if (root==NULL) return NULL;
            if(e<root->element()) return findhelp(root->left(),e);
            else if(e>root->element()) return findhelp(root->right(),e);
            else return root->element();
        }

        //打印BST树
        void printhelp(BSTNode<E>* root,int level) const
        {
            if(root==NULL) return ;
            printhelp(root->right(),level+1);
            for(int i=0;i<level;i++)
                cout<<"  ";
            cout<<root->element()<<"\\n";
            printhelp(root->left(),level+1);
        }

    public:
        BST(){root=NULL;nodecount=0;}
        ~BST(){clearhelp(root);}

        BSTNode<E>* getRoot() {return this->root;}
        void insert(const E& e)
        {
            root=inserthelp(root,e);
            nodecount++;
        }

        E remove (const E&e)
        {
            E temp=findhelp(root,e);
            if (temp!=NULL)
            {
                root=removehelp(root,e);
                nodecount--;
            }
            return temp;
        }

        //删除根结点
        E removeAny()
        {
            if(root!=NULL)
            {
                E temp=root->element();
                root=rempvehelp(root,root->element());
                nodecount--;
                return temp;
            }
            else return NULL;
        }

        E find(const E&e) const {return findhelp(root,e);}
        int size() {return nodecount;}

        void print() const
        {
            if (root==NULL) cout<<"The BST is empty.\\n";
            else printhelp(root,0);
        }    
};

main.cpp:

#include"BST.h"
#include"BSTNode.h"
#include<iostream>
#include<cstdlib>
using namespace std;
//求所有结点之和
int sum(BSTNode<int>* root,int &num)
{
    if(root==NULL) return -1;
    num+=root->element();
    sum(root->left(),num);
    sum(root->right(),num);
    return num;
}
//寻找所以比指定值小的所有的数
int findSmallCount(BSTNode<int>* root,int k,int &count)
{
    if(root==NULL) return 0;
    if(k>=root->element()) count++;
    findSmallCount(root->left(),k,count);
    if(k<root->element()) return count;
    findSmallCount(root->right(),k,count);
    return count;
}
//寻找在两数之间的数
void print(BSTNode<int>* root,int min,int max)
{
    if(root==NULL) return ;
    print(root->left(),min,max);
    if(root->element()<max && root->element()>min) cout<<root->element()<<" ";
    print(root->right(),min,max);
}

int main()
{
    int n=0;
    cout<<"Please input the number of BST:"<<endl;
    BST<int> bst;
    cin>>n;
    cout<<"Please input the BSTNode:"<<endl;
    while(n)
    {
        int m=0;
        cin>>m;
        bst.insert(m);
        n--;
    }
    //打印BST
    bst.print();
    int num=0;
    BSTNode<int>* root=bst.getRoot();
    cout<<"sum = "<<sum(root,num)<<endl;

    int count=0;
    int k=0;
    cout<<"Please input the k:"<<endl;
    cin>>k;
    cout<<"There are "<<findSmallCount(root,k,count)<<" numbers which are lower than "<<k<<endl;


    int min=0,max=0;
    cout<<"Please enter a minimum value and then a maximum value:"<<endl;
    cin>>min>>max;
    print(root,min,max);
    system("pause");
    return 0;
}

三.结果展示

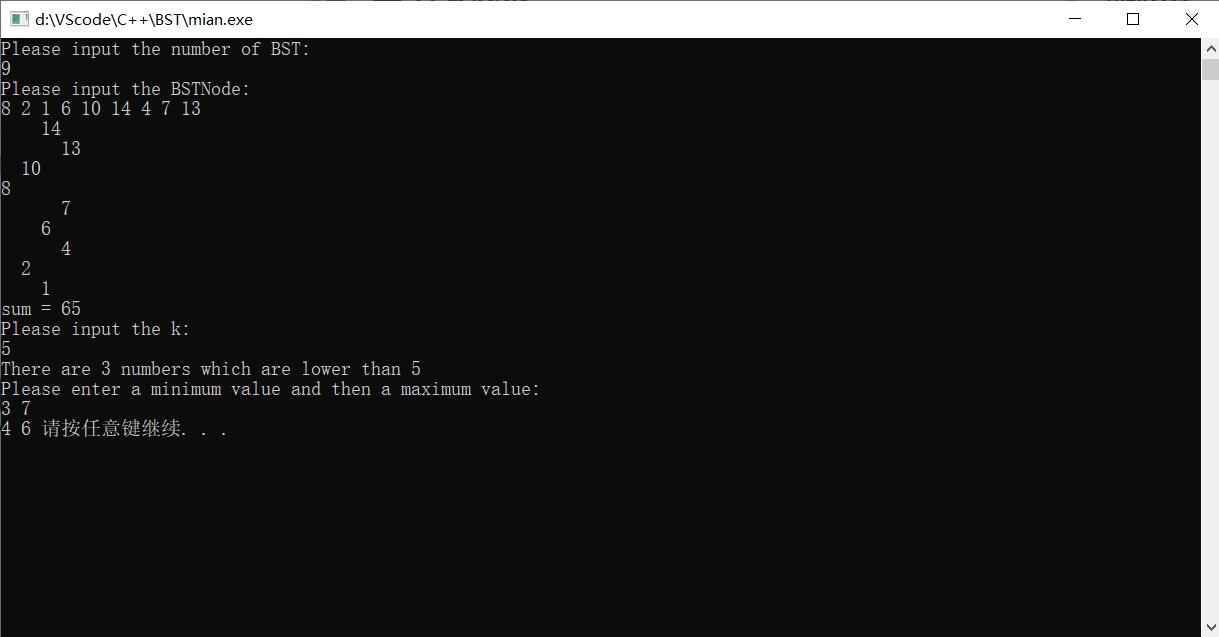
将打印出来的BST顺时针旋转90°就可以看到标准的BST，在主函数中依次实现了建树、打印树、求和、查找小于k的数的个数、查找位于两个数之间的数。

其他比如删除、查找等操作大家可以自行实现！