C++图(邻接矩阵实现+必要算法)
Posted 桃陉
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C++图(邻接矩阵实现+必要算法)相关的知识,希望对你有一定的参考价值。
一.基础知识
说起图来大家都很容易理解,图就是由若干顶点以及连接顶点的边所构成的图形。如下图所示:
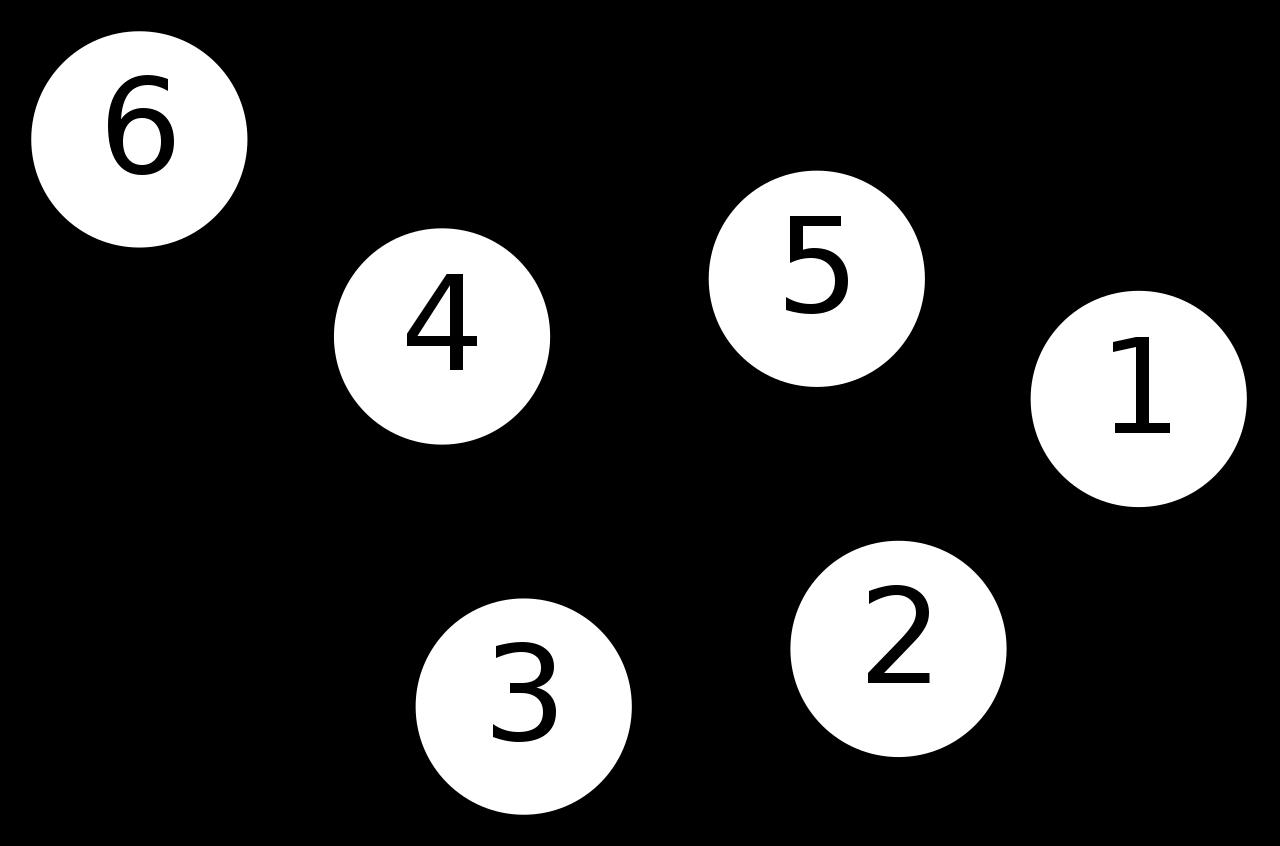
接下来我们介绍一些图中的基本概念:
∙ \\bullet ∙ 顶点(Vertex):自面意思,比如说上图的1、2、3、4、5、6
∙ \\bullet ∙ 边(edge):自面意思,连接两个顶点的线条
∙ \\bullet ∙ 权重(weight):每条边上所赋的一个值
∙ \\bullet ∙ 无向图:顶点之间没有连接方向,我们重点讨论的就是无向图。(拓扑排序中使用有向图)
∙ \\bullet ∙ 路径:路径就是从一个节点到另一个节点所经过线路,比如说从1到6有两条路径(针对无向图)分别为:1-5-4-6、1-2-3-4-6。
图的表示方式一共有两种:
∙
\\bullet
∙ 邻接矩阵表示:使用二维矩阵,用行row中的一个数表示一个顶点,列col中的一个数表示另一个顶点。对应的值为它们连线的权重,如果没有连接,那么置为0或者无穷大。在具体实现中我将矩阵多增加了一行一列,这样操作时可以使下标从1开始,这里我们将权重都先记为1,上图的邻接矩阵如下:

很容易可以发现,邻接矩阵是对称矩阵。
∙ \\bullet ∙ 邻接表表示:使用链表数组,每个顶点引出取一条链表,每个节点包含它们的下标值、权重与下一个节点地址。类似于我之前说的 哈希表的链表数组实现,只是需要多加一个权重而已。
下面简略提一下我们所实现的图中的一些算法:
| 函数名称 | 作用 |
|---|---|
| 深度优先搜索DFS算法 | 对图进行遍历 |
| 广度优先搜索BFS算法 | 对图进行遍历 |
| 单源最短路径Dijkstra算法 | 从一个点出发到各个点的最短路径 |
| 最小生成树Prim算法 | 用n-1条边连接n个顶点,使得总体权重最小 |
下面我们会详细的介绍每个算法的实现!
二.分步实现代码
定义的一些常量:
VISITED表示该顶点已访问,UNVISITED表示该顶点未经访问,INF用来模拟上面所说的无穷大,也就是表示这里没有边连接。
const int VISITED=1;
const int UNVISITED=0;
const int INF = 10000;
图的虚类表示一些图中需要实现的基本函数:
//图的虚类
class Graph
{
private:
void operator = (const Graph&) {} //赋值
Graph(const Graph&) {} //拷贝函数
public:
Graph(){}
virtual ~Graph(){}
virtual void Init(int n)=0; //初始化
virtual int n()=0; //返回图的顶点数
virtual int e()=0; //返回图的边数
virtual int first(int v)=0; //返回第一个
virtual int next(int v,int w)=0; //返回下一个
virtual void setEdge(int val,int v2,int wght)=0; //给两个点之间的边来设计权重
virtual void delEdge(int v1,int v2)=0; //删掉两点之间的边
virtual bool isEdge(int i,int j)=0; //判断是否为存在的边
virtual int weight(int v1,int v2)=0; //取权重
virtual int getMark(int v)=0; //取出标记
virtual void setMark(int v,int val)=0; //进行标记
};
边的结构体:
struct edge
{
int start; //起始点
int end; //终点
int wt; //权重
};
图中承接虚类的基本函数实现:
//使用邻接矩阵进行存储
class Graphm: public Graph
{
private:
int numVertex,numEdge; //点数、边数
int **matrix; //邻接矩阵
int *mark; //指向存放有无访问该点的数组
bool ishui; //判断是否为回路
public:
//构造函数
Graphm(int numVert){Init(numVert);}
//析构函数
~Graphm()
{
delete []mark;
for(int i=0;i<numVertex;i++)
delete []matrix[i];
delete matrix;
}
//初始化函数
void Init(int n)
{
int i;
numVertex=n;
numEdge=0;
mark=new int[n];
//开始都标记为为访问
for (i=0;i<numVertex;i++)
mark[i]=UNVISITED;
matrix=(int**) new int*[numVertex];
for (i=0;i<numVertex;i++)
matrix[i]=new int[numVertex];
for(i=0;i<numVertex;i++)
for(int j=0;j<numVertex;j++)
matrix[i][j]=0;
ishui=true;
}
//取出图中顶点数
int n(){return numVertex;}
//取出图中的边数
int e(){return numEdge;}
//返回v的第一个邻居
int first(int v)
{
for(int i=0;i<numVertex;i++)
if(matrix[v][i]!=0) return i;
return numVertex; //如果不存在,就返回n
}
//返回v在w之后的第一个邻居
int next(int v,int w)
{
for (int i=w+1;i<numVertex;i++)
if(matrix[v][i]!=0) return i;
return numVertex;
}
//设置v1和v2之间的边权重为wt
void setEdge(int v1,int v2,int wt)
{
if(matrix[v1][v2]==0) numEdge++; //如果没有边,则增加一条
matrix[v1][v2]=matrix[v2][v1]=wt;
}
//删除v1和v2之间的边
void delEdge(int v1,int v2)
{
if(matrix[v1][v2]!=0) numEdge--;
matrix[v1][v2]=0;
}
//判断v1和v2间是否有边
bool isEdge(int v1,int v2)
{
return matrix[v1][v2]!=0;
}
int weight(int v1,int v2) {return matrix[v1][v2];}
int getMark(int v) {return mark[v];}
void setMark(int v,int val) {mark[v]=val;}
void initMark(){for(int i=0;i<numVertex;i++) mark[i]=UNVISITED;}
//打印邻接矩阵
void print()
{
for (int i=0;i<numVertex;i++){
for (int j=0;j<numVertex;j++)
cout<<matrix[i][j]<<" ";
cout<<endl;
}
}
};
深度优先搜索遍历图:
给定了图以及开始的顶点v,如果顶点v没有被访问过,那么我们输出v并计数加1,然后将顶点v置为已访问。然后以v为顶点开始寻找一条路径进行搜索,搜索到底时退后一步寻找其他路径,直到所有顶点都被访问为止。
在下面代码中的具体实现就是使用了for循环,递归调用函数。
void DFS(Graphm* G,int v)
{
if(G->getMark(v)==UNVISITED)
{
if(num==G->n()-2) cout<<v;
else cout<<v<<" ";
num++;
}
G->setMark(v,VISITED);
for(int w=G->first(v);w<G->n();w=G->next(v,w))
if(G->getMark(w)==UNVISITED)
DFS(G,w);
}
广度优先搜索遍历图:
使用了队列这一数据结构,同样是给定图以及开始顶点start,我们想将start存入队列进行访问后,将start出队并将其所有相邻顶点入队,重复此操作直到所有顶点访问完成为止。
注意:在代码最后我们加了一个判断图中是否存在为访问顶点的判断,当存在时说明图中有环。
void BFS(Graphm* G,int start)
{
int v,w;
queue<int>q;
int cnt=0;
q.push(start);
G->setMark(start,VISITED);
while (!q.empty())
{
v=q.front();
if(cnt==G->n()-2) cout<<v;
else cout<<v<<" ";
q.pop();
for (w=G->first(v);w<G->n();w=G->next(v,w))
if(G->getMark(w)==UNVISITED)
{
G->setMark(w,VISITED);
q.push(w);
}
cnt++;
}
//BFS搜索后判断是否有未访问的点
for(int i=1;i<numVertex;i++)
{
if(G->getMark(i)==UNVISITED) {ishui=false;break;}
}
}
求单源最短路径:
给定图以及存放路径长度的数组D、开始顶点s、存放具体路径的字符串数组n。先挑选一条从s出发的边,然后比较是直接连接更近还是走其他的边更近,经过比较后选出两点间最短的路径。
void Dijkstra(Graph* G,int *D,int s,string n[])
{
int v,i,w;
for(i=0;i<G->n();i++)
{
v=minVertex(G,D);
if(D[v]==INF) return;
G->setMark(v,VISITED);
for(w=G->first(v);w<G->n();w=G->next(v,w))
{
if(D[w]>(D[v]+G->weight(v,w)))
{
D[w]=D[v]+G->weight(v,w);
n[w]=n[v]+" "+ std::to_string(w);
}
}
}
}
//取最小
int minVertex(Graphm* G,int* D)
{
int i,v=-1;
for (i=0;i<G->n();i++)
if(G->getMark(i)==UNVISITED) {v=i;break;}
for (i++;i<numVertex;i++)
if((G->getMark(i)==UNVISITED) && (D[i]<D[v]))
v=i;
return v;
}
求最小生成树:
给定图以及开始顶点s、开始顶点s与各点距离数组D、表示边的数组e。首先开始添加连接顶点s的一条最短边,然后将这两个顶点作为一个整体,添加连接它们的一条最短边,一直进行扩充直到包含所有顶点为止。
void Prim(Graphm* G,int *D,int s,struct edge e[])
{
int *V=NULL;
V = new int[G->n()];
// int V[G->n()]={0};
int ans=0;
int i,w;
for(i=1;i<G->n();i++)
{
int v=minVertex(G,D);
G->setMark(v,VISITED);
if(v!=s)
{
// cout<<V[v]<<" "<<v<<" "<<G->weight(v,V[v])<<endl;
if(V[v]<v) {e[ans].start=V[v],e[ans].end=v,e[ans].wt=G->weight(V[v],v);}
else
{e[ans].end=V[v],e[ans].start=v,e[ans].wt=G->weight(V[v],v);}
ans++;
}
if(D[v]==INF) return;
for(w=G->first(v);w<G->n();w=G->next(v,w))
{
if(D[w]>G->weight(v,w))
{
D[w]=G->weight(v,w);
V[w]=v;
}
}
}
}
int minVertex(Graphm* G,int* D)
{
int i,v=-1;
for (i=0;i<G->n();i++)
if(G->getMark(i)==UNVISITED) {v=i;break;}
for (i++;i<numVertex;i++)
if((G->getMark(i)==UNVISITED) && (D[i]<D[v]))
v=i;
return v;
}
三.完整代码
Graph.h:
#ifndef _GRAPH_H_
#define _GRAPH_H_以上是关于C++图(邻接矩阵实现+必要算法)的主要内容,如果未能解决你的问题,请参考以下文章