PRML 1.3 模型选择 1.4 维度灾难

Posted 2021-08-08 Real&Love

PRML 1.3 模型选择 1.4 维度灾难

在我们的模型选择中，我们可以通过交叉验证的方法来训练模型。但是交叉验证的缺点也很明显，随着训练次数随“分割”的增加，训练时间也是很大的消耗。而且随着模型参数的每一次修改，这些分割的模型也会再一次修改。PRML书上还讲述了一种方法。

1.3.1 AIC(赤池信息准则)

赤池信息量准则（英语：Akaike information criterion，简称AIC）是评估统计模型的复杂度和衡量统计模型“拟合”资料之优良性（英语：Goodness of Fit，白话：合身的程度）的一种标准，是由日本统计学家赤池弘次创立和发展的。赤池信息量准则建立在信息熵的概念基础上
$$AIC=2K-2ln(L)$$
其中：k是参数的数量，L是似然函数

结论

• 参数越少，AIC值越小，模型越好
• 样本数越多，AIC值越小，模型越好

1.3.2 BIC(贝叶斯信息准则)

BIC的惩罚项比AIC的大，考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高
$$BIC=kln(n)-2ln(L)$$

说明： 此书后面第4章会更详细的将AIC和BIC。

下面时sklearn中的例子节选

import time

import numpy as np
import matplotlib.pyplot as plt

from sklearn.linear_model import LassoCV, LassoLarsCV, LassoLarsIC
from sklearn import datasets

diabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target

rng = np.random.RandomState(42)
X = np.c_[X, rng.randn(X.shape[0], 14)]  # add some bad features

# normalize data as done by Lars to allow for comparison
X /= np.sqrt(np.sum(X ** 2, axis=0))

# #############################################################################
# LassoLarsIC: least angle regression with BIC/AIC criterion

model_bic = LassoLarsIC(criterion='bic')
t1 = time.time()
model_bic.fit(X, y)
t_bic = time.time() - t1
alpha_bic_ = model_bic.alpha_

model_aic = LassoLarsIC(criterion='aic')
model_aic.fit(X, y)
alpha_aic_ = model_aic.alpha_

def plot_ic_criterion(model, name, color):
    alpha_ = model.alpha_
    alphas_ = model.alphas_
    criterion_ = model.criterion_
    plt.plot(-np.log10(alphas_), criterion_, '--', color=color,
             linewidth=3, label='%s criterion' % name)
    plt.axvline(-np.log10(alpha_), color=color, linewidth=3,
                label='alpha: %s estimate' % name)
    plt.xlabel('-log(alpha)')
    plt.ylabel('criterion')

plt.figure()
plot_ic_criterion(model_aic, 'AIC', 'b')
plot_ic_criterion(model_bic, 'BIC', 'r')
plt.legend()
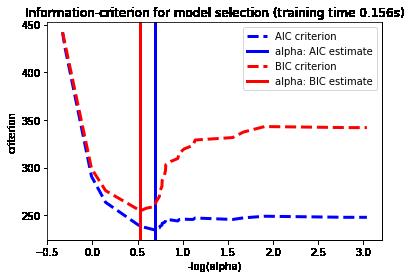
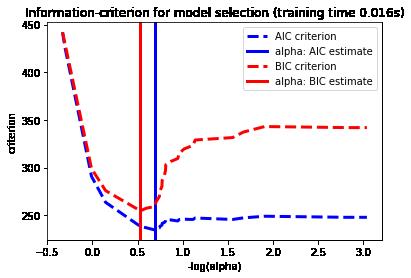
plt.title('Information-criterion for model selection (training time %.3fs)'
          % t_bic)
plt.show()

1.4 维度灾难

---

1.4.1 什么是维度灾难

维度也就是数据集的特征，如果遵循奥卡姆剃刀原则， 数据的特征越简单越好。当维度很高时，某些重要的特征便会隐藏在一些无关的特征中；另一方面，训练数据时，对时间复杂度，和参数估计也是一种考验； 而且如果不对特征维度进行处理，那么一些具有相关性的特征，我们不做处理，模型的效果肯定是不好的。（例如：回归问题中的多重共线性）

1.4.2 解决方法

• 主成分分析法PCA
• 线性判别法LDA
• 奇异值分解简化数据
• 拉普拉斯特征映射
• Lassio缩减系数法
• 小波分析法