PRML 1.5 决策论
Posted Real&Love
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了PRML 1.5 决策论相关的知识,希望对你有一定的参考价值。
PRML 1.5 决策论
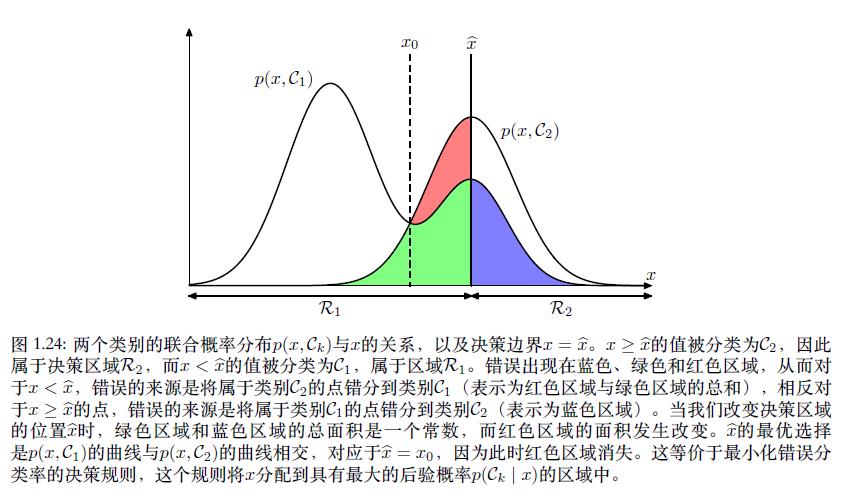
1.5.1 最小化错误分类率(Minimizing the misclassification rate)
对监督学习中的分类问题来讲,我们需要一个“规则”,把每一个
x
x
x分到合适的类别中去。这个“规则”会把输入空间分成不同的区域,这种区域叫做决策区域(decision region),而决策区域的边界叫做决策边界或者叫决策面。如上图所示,如果我们将属于
C
1
C_1
C1类的值分到了
C
2
C_2
C2类中,那么我们就犯了一个错误。这种发生的概率如下:
p
(
m
i
s
t
a
k
e
)
=
p
(
x
∈
R
1
,
C
2
)
+
p
(
x
∈
R
2
,
C
1
)
=
∫
R
1
p
(
x
,
C
2
)
d
x
+
∫
R
2
p
(
x
,
C
1
)
d
x
p(mistake) = p(x\\in R_1, C_2)+p(x\\in R_2, C_1)=\\int_{R_1}p(x,C_2)\\mathrm{d} x+\\int_{R_2}p(x,C_1)\\mathrm{d} x
p(mistake)=p(x∈R1,C2)+p(x∈R2,C1)=∫R1p(x,C2)dx+∫R2p(x,C1)dx
我们当然希望将错误降到最小,即最小化
p
(
m
i
s
t
a
k
e
)
p(mistake)
p(mistake)。根据乘积规则,
p
(
x
,
C
k
)
=
p
(
C
k
∣
x
)
p
(
x
)
p(x, C_k)=p(C_k|x)p(x)
p(x,Ck)=p(Ck∣x)p(x)
对最小化
p
(
x
,
C
k
)
p(x, C_k)
p(x,Ck),那么需要最小化
p
(
C
k
∣
x
)
p(C_k|x)
p(Ck∣x)。
对于更⼀般的K类的情形,最大化正确率会稍微简单⼀些,即最大化下式
p
(
correct
)
=
∑
k
=
1
K
p
(
x
∈
R
k
,
C
k
)
=
∑
k
=
1
K
∫
R
k
p
(
x
,
C
k
)
dx
p ( \\text{correct} ) =\\sum_{k=1}^Kp ( \\text{x}\\in\\mathcal{R}_k,\\mathcal{C}_k ) =\\sum_{k=1}^K\\int_{\\mathcal{R}_k} p ( \\text{x},\\mathcal{C}_k ) \\text{dx}
p(correct)=k=1∑Kp(x∈Rk,Ck)=k=1∑K∫Rkp(x,Ck)dx
1.5.2 最小化期望损失(Minimizing the expected loss)
书中举了一个对癌症病人分类的例子,我这里简单阐述一下。分类问题我们都会出现两种错误。一,给没有患癌症的病人错误地诊断为癌症,二、给患了癌症的病人诊断为健康。我们给出如下混淆矩阵:

接着,我们引出损失矩阵(loss matrix),例如癌症这个例子,作者自己定义了一个损失矩阵,如下所示
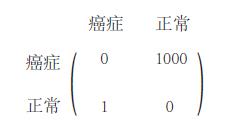
如上图所示,我们将正常人诊断为癌症的错误损失记为1,而将癌症诊断为正常的错误损失记为1000。常见的损失函数如下所示
(1) 0-1损失函数
L
(
Y
,
f
(
X
)
)
=
{
1
,
Y
≠
f
(
X
)
0
,
Y
=
f
(
X
)
L(Y,f(X))=\\left\\{ \\begin{array}{c}1, Y\\neq f(X) \\\\0, Y= f(X)\\end{array}\\right.
L(Y,f(X))={1,Y=f(X)0,Y=f(X)
(2) 平方损失函数
L
(
Y
,
f
(
X
)
)
=
(
Y
−
f
(
X
)
)
2
L(Y,f(X))=(Y-f(X))^2
L(Y,f(X))=(Y−f(X))2
(3) 绝对损失函数
L
(
Y
,
f
(
X
)
)
=
∣
Y
−
f
(
X
)
∣
L(Y,f(X))=|Y-f(X)|
L(Y,f(X))=∣Y−f(X)∣
(4)对数损失函数
L
(
Y
,
P
(
Y
∣
X
)
)
=
−
l
o
g
P
(
Y
∣
X
)
L(Y,P(Y|X))=-logP(Y|X)
L(Y,P(Y∣X))=−logP(Y∣X)
1.5.3 拒绝选项(The reject option)
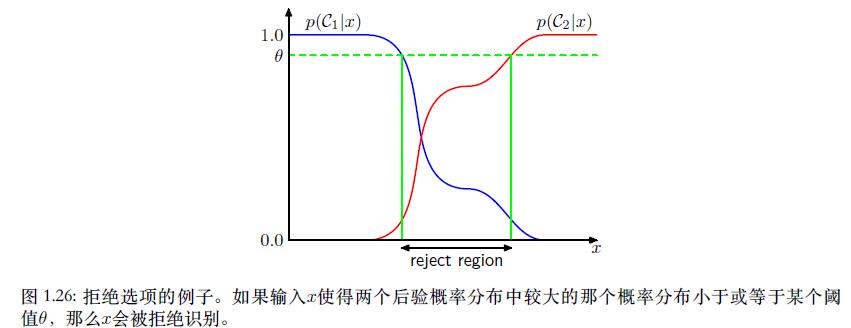
例如,在我们假想的医疗例⼦中,⼀种合适的做法是,使⽤⾃动化的系统来对那些⼏乎没有疑问的X光片进行分类,然后把不容易分类的X光片留给医学专家。为了达到这个目的,我们引入一个阈值 θ \\theta θ拒绝后验概率 p ( C k ∣ x ) p(C_k|x) p(Ck∣x)的最大值小于等于 θ \\theta θ的那些样本。
1.5.4 推断和决策
接着下面讲了生成式模型(generative models)、判别式模型(discriminative models)、异常检测(novelty detection)
(a) 生成式模型(generative models)
常见的生成式模型有:
- 朴素贝叶斯
- 隐马尔科夫模型
比如对训练集来讲,我们通过训练得到此数据集的分布,在根据决策论来确定新数据的类别。生成式模型就是生成数据分布的模型。也就是说我们需要对输入和输出进行“建模”。
(b) 判别式模型(discriminative models)
常见的判别式模型如下:
- kNN
- 决策树
- 逻辑回归
- SVM
判别式模型我们需要确定 p ( C k ∣ x ) p(C_k|x) p(Ck∣x),接着用决策论来对新的输入 x x x进行分类。
1.5.5 回归问题中的损失函数
在回归问题中, 损失函数的一个通常的选择是平方损失,
L ( Y , f ( X ) ) = ( Y − f ( X ) ) 2 L(Y,f(X))=(Y-f(X))^2 L(Y,f(X))=(Y−f(X))2
那么期望损失函数可以写成
E
[
L
]
=
∬
{
y
(
x
)
−
t
}
2
p
(
x
,
t
)
d
x
d
t
E[L]=\\iint\\left \\{y(x)-t \\right \\}^2p(x,t)dxdt
E[L]=∬{y(x)−t}2p(x,t)dxdt
一般我们的目标是寻找一个
y
(
x
)
y(x)
y(x)来最小化我们的
E
[
L
]
E[L]
E[L]函数,所以我们用变分法,求解
y
(
x
)
y ( \\text{x} )
y(x) 的最优解
那么有
∂
E
[
L
]
∂
y
(
x
)
=
2
∫
{
y
(
x
)
−
t
}
p
(
x
,
t
)
d
t
=
0
\\frac{\\partial E[L]}{\\partial y(x)}=2\\int\\left \\{y(x)-t \\right\\}p(x,t)dt=0
∂y(x)∂E[L]=2∫{y(x)−t}p(x,t)dt=0
利用加和规则和乘积规则,求解
y
(
x
)
y ( \\text{x} )
y(x) 的最优解
y
(
x
)
=
∫
t
p
(
x
,
t
)
d
t
p
(
x
)
=
∫
t
p
(
t
∣
x
)
d
t
=
E
t
[
t
∣
x
]
y(x)=\\frac{\\int tp(x,t)dt}{p(x)}=\\int tp(t|x)dt=E_t[t|x]
y(x)=以上是关于PRML 1.5 决策论的主要内容,如果未能解决你的问题,请参考以下文章