PRML 1.6 信息论
Posted Real&Love
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了PRML 1.6 信息论相关的知识,希望对你有一定的参考价值。
PRML 1.6 信息论
信息内容的度量以来于某个概率分布
p
(
x
)
p(x)
p(x)。为了表达我们接受到的信息,我们寻找一个函数
h
(
x
)
h(x)
h(x),它是概率
p
(
x
)
p(x)
p(x)的单调函数。如果我们有两个不相关的事件
x
x
x和
y
y
y那么我们观察到两个事件同时发生接收到的信息之和为
h
(
x
,
y
)
=
h
(
x
)
+
h
(
y
)
h(x,y)=h(x)+h(y)
h(x,y)=h(x)+h(y)
而两个事件的概率关系:
p
(
x
,
y
)
=
p
(
x
)
p
(
y
)
p(x, y) = p(x)p(y)
p(x,y)=p(x)p(y)
可以看出概率关系和信息量的多少有一定的对数关系,因此:
h
(
x
)
−
l
o
g
2
p
(
x
)
h(x)-log_2p(x)
h(x)−log2p(x)
其中负号保证了信息为正数或者是零。不难看出,概率越低(不确定性越大)信息量越多(大),
h
(
x
)
h(x)
h(x)的单位是比特(bit,binary digit)
接着,我们用熵来评价整个随机变量x平均的信息量,而平均最好的量度就是随机变量的期望,即熵的定义如下:
H
[
x
]
=
−
∑
x
p
(
x
)
l
o
g
2
p
(
x
)
H[x]=-\\sum_{x}p(x)log_2p(x)
H[x]=−x∑p(x)log2p(x)
| header 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 随机变量 | a | b | c | d | e | f | g | h | |
| 状态 | 1/2 | 1/4 | 1/8 | 1/16 | 1/64 | 1/64 | 1/64 | 1/64 |
根据公式可以计算出熵为2bit
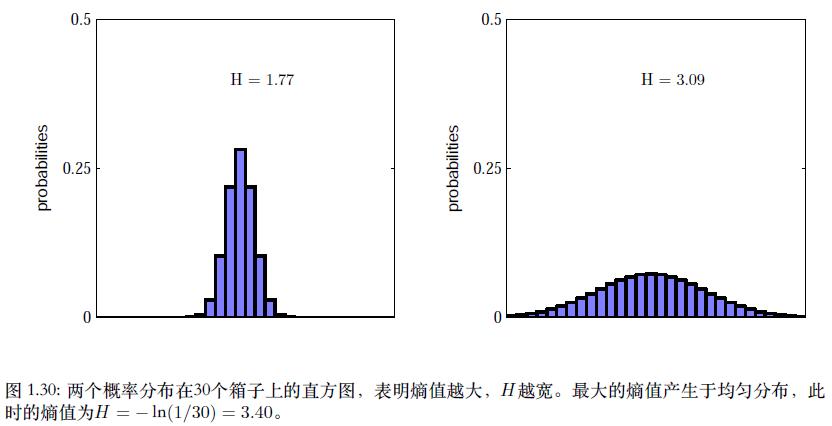
从现在开始,我们会将熵的定义中的对数变成自然对数,这种情况下,熵的度量的单位是nat,而不是bit。两者的差别是⼀个ln 2的因子。
如上图所示,如果分布 p ( x i ) p(x_i) p(xi)在几个值周围有尖锐的峰值,熵就会相对降低,如果相对平稳地跨过许多值,那么熵就会很高。
1.6.1 相对熵和互信息
我们已经知道了,信息熵是衡量随机变量或者整个系统的不确定性,不确定性越大,熵越大,呈正相关关系。
每一个系统都会有一个真实的概率分布,我们根据真实的概率分布找到一个最优的策略,以最小的代价消除系统的不确定性,这个"大小"就是信息熵。而如果我们以非真实的分布来选择策略来消除系统的不确定性,这个"大小"就是交叉熵。
∑
k
=
1
N
p
k
log
2
1
q
k
\\sum_{k=1}^Np_k\\log_2\\frac{1}{q_k}
k=1∑Npklog2qk1
其中 p k p_k pk表示真实分布,而 q k q_k qk表示非真实分布。交叉熵越低,则策略越好,所以在机器学习中,我们需要最小化交叉熵,这样我们的策略才会越接近最优策略。
我们又如何去衡量不同策略之间的差异呢?相对熵,顾名思义,相对熵是用来衡量两个取值为正的函数或概率分布之间的差异
K
L
(
p
∣
∣
q
)
=
−
∫
p
(
x
)
ln
q
(
x
)
d
x
−
(
−
∫
p
(
x
)
ln
p
(
x
)
d
x
)
K
L
(
p
∣
∣
q
)
=
−
∫
p
(
x
)
ln
{
q
(
x
)
p
(
x
)
}
d
x
KL(p||q)=-\\int p(x)\\ln q(x) \\mathrm{d}x - (-\\int p(x)\\ln p(x) \\mathrm{d}x) \\\\\\\\ KL(p||q)= -\\int p(x)\\ln\\{\\frac{q(x)}{p(x)}\\}\\mathrm{d}x
KL(p∣∣q)=−∫p(x)lnq(x)dx−(−∫p(x)lnp(x)dx)KL(p∣∣q)=−∫p(x)ln{p(x)q(x)}dx
这被称为分布p(x)和分布q(x)之间的相对熵(relative entropy),或者叫KL散度(Kullback and Leibler, 1951)。相对熵不是一个对称量,即
K
L
(
p
∣
∣
q
)
≠
K
L
(
q
∣
∣
p
)
KL(p||q) \\neq KL(q||p)
KL(p∣∣q)=KL(q∣∣p)
- 先介绍凸函数(convex function)的概念
如果⼀个函数具有如下性质:每条弦都位于函数图像或其上⽅(如下图所⽰),那么我们说这个函数是凸函数。
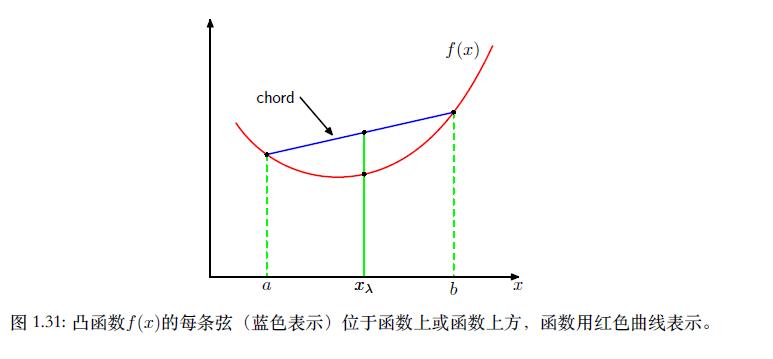
如图所示,我们可以将位于 [ a , b ] [a, b] [a,b]之间的任何一个 x x x的值都可以写成 λ a + ( 1 − λ ) b \\lambda a+(1-\\lambda)b λa+(1−λ)b,其中 0 ≤ λ ≤ 1 0\\leq \\lambda \\leq 1 0≤λ≤1,弦上对应的点可以写成 λ f ( a ) + ( 1 − λ ) f ( b ) \\lambda f(a)+(1-\\lambda)f(b) λf(a)+(1−λ)f(b)。函数对应的值可以写为 f ( λ a + ( 1 − λ ) b ) f(\\lambda a + (1-\\lambda)b) f(λa+(1−λ)b)。所以凸函数具有以下的性质:
f ( λ a + ( 1 − λ ) b ) ≤ λ a + ( 1 − λ ) b f(\\lambda a + (1-\\lambda)b)\\leq\\lambda a+(1-\\lambda)b f(λa+(1−λ)b)≤λa+(1−λ)b
典型的凸函数有: x 2 x^2 x2, x ln x ( x > 0 ) x\\ln x (x>0) xlnx(x>0)
现在要证明, K L KL KL散度满足 K L ( p ∣ ∣ q ) ≥ 0 KL(p||q)\\geq0 KL(p∣∣q)≥0,并且当且仅当 p ( x ) = q ( x ) p(x)=q(x) p(x)=q(x)时等号成立。
使用归纳法,可以证明凸函数满足:
f ( ∑ i = 1 M λ i x i ) ≤ ∑ i = 1 M λ i f ( x i ) f(\\sum^M_{i=1}\\lambda_i x_i)\\leq \\sum^M_{i=1}\\lambda_if(x_i) f(i=1∑Mλixi)≤i=1∑Mλif(xi)
如果将 λ i \\lambda_i λi看成取值为 x i {x_i} xi的离散变量 x x x的概率分布,那么上面的公式可以写成:
f ( E [ x ] ) ≤ E [ f ( x ) ] f(E[x])\\leq E[f(x)] f(E[x])≤E[f(x)]
就是Jensen不等式,即函数的期望大于期望的函数。
对连续变量,Jensen不等式的形式为
f
(
∫
x
p
(
x
)
d
x
)
≤
∫
f
(
x
)
p
(
x
)
d
x
f(\\int xp(x)\\mathrm {d}x) \\leq \\int f(x)p(x)\\mathrm {d}x
f(∫xp(x)dx)≤∫f(x)p(x)dx
那么对 K L KL KL散度,我们有:
K L ( p ∣ ∣ q ) = − ∫ p ( x ) ln q ( x ) p ( x ) d x ≥ − ln ∫ q ( x ) d x = 0 KL(p||q)=-\\int p(x)\\ln{\\frac{q(x)}{p(x)}}\\mathrm{d}x \\geq -\\ln \\int q(x) \\mathrm{d}x=0 KL(p∣∣q)=−∫p(x)lnp(x)以上是关于PRML 1.6 信息论的主要内容,如果未能解决你的问题,请参考以下文章