三点定圆原理与C++实现
Posted 借我十斤肉
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了三点定圆原理与C++实现相关的知识，希望对你有一定的参考价值。
1 原理
根据我们小学二年级就学过的三点定圆定理：
不 共 线 的 三 个 点 可 唯 一 确 定 一 个 圆 不共线的三个点可唯一确定一个圆 不共线的三个点可唯一确定一个圆
且，不共线的三点相互连接必然构成一个三角形，这个三角形称为圆的内接三角形，这个圆称为三角形的外接圆。三角形三边垂直平分线的交点即为三角形外接圆的圆心。
有了以上知识，由不共线的三个点确定一个圆就非常easy了
已知平面中不共线的三点
A
(
x
1
,
y
1
,
z
1
)
A(x_1,y_1,z_1)
A(x1,y1,z1)，
B
(
x
2
,
y
2
,
z
2
)
B(x_2,y_2,z_2)
B(x2,y2,z2)，
C
(
x
3
,
y
3
,
z
3
)
C(x_3,y_3,z_3)
C(x3,y3,z3)，互相连接构成三角形 ΔABC，
L
a
b
L_{ab}
Lab，
L
b
c
L_{bc}
Lbc，
L
a
c
L_{ac}
Lac 分别为三条边的垂直平分线，且相交于一点
O
O
O，该交点即为外接圆圆心。
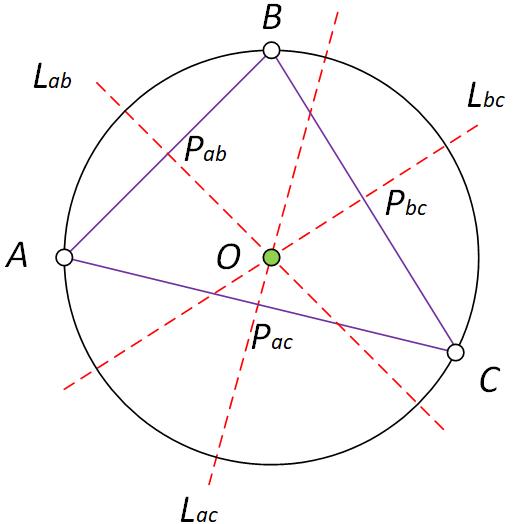
三角形三边斜率：
{
k
a
b
=
y
2
−
y
1
x
2
−
x
1
k
b
c
=
y
3
−
y
2
x
3
−
x
2
k
a
c
=
y
3
−
y
1
x
3
−
x
1
\\begin{cases} k_{ab}=\\cfrac {y_2-y_1}{x_2-x_1}\\\\ k_{bc}=\\cfrac {y_3-y_2}{x_3-x_2}\\\\ k_{ac}=\\cfrac {y_3-y_1}{x_3-x_1}\\\\ \\end{cases}
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧kab=x2−x1y2−y1kbc=x3−x2y3−y2kac=x3−x1y3−y1
三边中点:
P
a
b
(
x
1
+
x
2
2
，
y
1
+
y
2
2
)
,
P
b
c
(
x
2
+
x
3
2
，
y
2
+
y
3
2
)
,
P
a
c
(
x
1
+
x
3
2
，
y
1
+
y
3
2
)
P_{ab}(\\cfrac {x_1+x_2}{2}，\\cfrac {y_1+y_2}{2}), P_{bc}(\\cfrac {x_2+x_3}{2}，\\cfrac {y_2+y_3}{2}), P_{ac}(\\cfrac {x_1+x_3}{2}，\\cfrac {y_1+y_3}{2})
Pab(2x1+x2，2y1+y2),Pbc(2x2+x3，2y2+y3),Pac(2x1+x3，2y1+y3)
根据直线的点斜式方程，可求三条垂直平分线方程如下：
{
L
a
b
=
y
−
y
1
+
y
2
2
+
1
k
a
b
(
x
−
x
1
+
x
2
2
)
=
0
L
b
c
=
y
−
y
2
+
y
3
2
+
1
k
b
c
(
x
−
x
2
+
x
3
2
)
=
0
L
a
c
=
y
−
y
1
+
y
3
2
+
1
k
a
c
(
x
−
x
1
+
x
3
2
)
=
0
\\begin{cases} L_{ab}=y-\\cfrac {y_1+y_2}{2}+\\cfrac {1}{k_{ab}}(x-\\cfrac {x_1+x_2}{2})=0\\\\ L_{bc}=y-\\cfrac {y_2+y_3}{2}+\\cfrac {1}{k_{bc}}(x-\\cfrac {x_2+x_3}{2})=0\\\\ L_{ac}=y-\\cfrac {y_1+y_3}{2}+\\cfrac {1}{k_{ac}}(x-\\cfrac {x_1+x_3}{2})=0\\\\ \\end{cases}
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Lab=y−2MATLAB 四点定球及三点定圆(完整代码)