PRML 2.1 二元变量

Posted 2021-08-08 Real&Love

PRML 2.1 二元变量

---

2.1.1 伯努利分布 Bernoulli

考虑抛一个损坏的硬币的实验， 如果抛正面为1， 抛反面为0， 那么有如下二元随机变量 x ∈ { 0 , 1 } x\\in\\{0,1\\} x∈{0,1}。因为硬币是损坏的，所以抛正反面的概率不一定相同，现在我们假设抛正面的概率是$\mu$，即$x=1$的概率为$\mu$。因此有：
$$p(x=1|\mu )=\mu p(x=0|\mu )=1-\mu$$
所以$x$的概率分布可以写成：
$$Bern(x|\mu )={\mu }^x(1-\mu {)}^{1-x}$$
这就是最简单的伯努利分布（0-1分布），x只能取0或者1

• 期望：
  $$E[X]=\mu$$

• 方差：
  $$Var[x]=\mu (1-\mu )$$

---

2.1.2 二项分布

现在我们假设有个$x$的观测集$D=x_1,...,x_N$，假设每次构造都是从$p(x|\mu )$中独立地抽取。构造$\mu$的似然函数如下：
$$p(D|\mu )=\prod _{n=1}^{N}p(x_n|\mu )=\prod _{n=1}^N{\mu }^{x_n}(1-\mu {)}^{1-x_n}$$

等式两边取对数有：
ln ⁡ p ( D ∣ μ ) = ∑ n = 1 N ln ⁡ p ( x n ∣ μ ) = ∑ n = 1 N { x n ln ⁡ μ + ( 1 − x n ) ln ⁡ ( 1 − μ ) } \\ln p(D|\\mu)=\\sum ^N_{n=1}\\ln p(x_n|\\mu)=\\sum ^N_{n=1}\\{x_n\\ln \\mu + (1-x_n)\\ln (1-\\mu)\\} lnp(D∣μ)=n=1∑N​lnp(xn​∣μ)=n=1∑N​{xn​lnμ+(1−xn​)ln(1−μ)}

另上式关于$\mu$的导数为零，那么得到最大似然的估计值：(建议自己推导一下)
$${\mu }_{ML}=\frac{1}{N}\sum _{n=1}^N{x}_n$$

如果我们把正面朝上（$x=1$）的观测的数量记为$m$，那么上述公式为:
$${\mu }_{ML}=\frac{m}{N}$$
因为我们只有$0,1$取值，所以就为$\frac{m}{N}$
$x=1$的观测出现$m$的概率分布，这被称为二项分布，在N此抛硬币的过程中，我们需要把所有获得$m$个正面朝上的方式加起来，那么得到：
$$Bin(m|N,\mu )=(\genfrac{}{}{0ex}{}{N}{m}){\mu }^m(1-{\mu }^{N-m})$$

• 期望
  $$E[m]=\sum _{m=0}^{N}mBin(m|N,\mu )=N\mu$$

• 方差
  $$Var[m]=\sum _{m=0}^N(m-E[m]{)}^{2}Bin(m|N,\mu )=N\mu (1-\mu )$$
  除了求和，我们也可以用积分的形式来证明

  下图给出了$N=10$,$\mu =0.25$的示意图

---

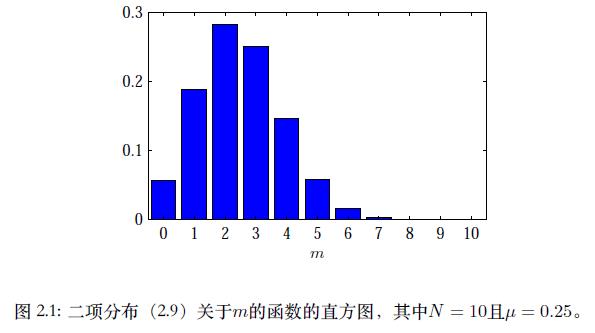
2.1.3 Beta分布

在书中，提出了这样一个问题，现假设我们抛3次硬币，碰巧三次都是正面朝上，那么依据二项分布${\mu }_{ML}=1$，这种情况下，最大似然的结果预测所有未来的观测都是正面朝上，对这种小规模的数据集比较容易出现过拟合，此时我们需要利用贝叶斯的观点来看待这个问题。

我们需要引入一个先验分布$Beta$分布
$$Beta(\mu |a,$$

PRML 学习: Polynomial Curve Fitting

PRML 学习: Polynomial Curve Fitting

PRML中文版（马春鹏）勘误表

PRML - Chapter 1: Introduction

PRML 1.2 概率论