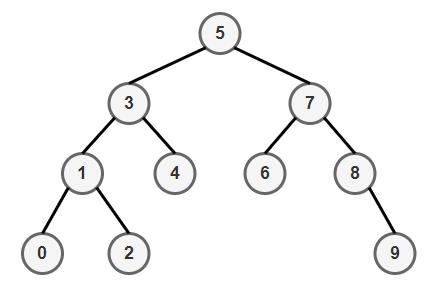
二叉搜索树(BST)的具体实现

Posted 2021-08-08 It‘s so simple

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二叉搜索树(BST)的具体实现相关的知识，希望对你有一定的参考价值。

1. BST树概念

二叉搜索树又称二叉排序树，它或者是一颗空树，或者具有以下的性质的二叉树：

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值。
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。
它的左右子树也分别为二叉搜索树。

对一颗二叉搜索树进行中序遍历，就可以按照从小到大的顺序，将各节点关键码排列起来，所以被称为二叉排序树。

BST的结构如下：


template<typename T>
class bstTree;

template<typename T>
class bstNode
{
	friend bstTree<T>;
    public:
    	explicit bstNode():left_(nullptr),right_(nullptr)
    	{}

        bstNode(T data) : data_(data),left_(nullptr),right_(nullptr)
    	{}
    	
        ~bstNode() {}

    private:
        T val_;
        bstNode* left_;
        bstNode* right_;
};

template<typename T>
class bstTree
{
    public:
        bstTree() : root_(nullptr)
        {}
        bstTree(vector<T> iv) : root_(nullptr)
        {
            for(const auto &e : iv)
                _Insert(root_,e);
        }
        ~bstTree() {}
        T& Max() const
        {
            return _Max(root_);
        }
        T& Min() const
        {
            return _Min(root_);
        }
        bstTree<T>* Search(const T& val) const
        {
            return _Search(root_,val);
        }
        bool Insert(const T& val)
        {
            return _Insert(root_,val);
        }
        bool Remove(const T& val)
        {
            return _Remove(root_,val);
        }
        
    protected:
        bool _Remove(bstTree<T>*& pos,const T& value);
        bool _Insert(bstNode<T>*& pos,const T& value);
        bstTree<T>* _Search(bstTree<T>*& pos,const T& value);
        T& _Min(bstNode<T>* pos);
        T& _Max(bstNode<T>* pos);

        
    private: 
        bstNode<T>* root_; 
};

2. BST接口的实现

2.1 寻找BST树中的结点（Search）

bstTree<T>* _Search(bstTree<T>*& pos,const T& value);

代码实现：

template<typename T>
bstTree<T>* bstTree<T>::_Search(bstTree<T>*& pos,const T& value)
{
	assert(pos != nullptr);

	if(val == pos->val_)
		return pos;
	else if(pos->val_> val)
		return Search(pos->left_,value);
	else
		return Search(pos->right_,value);
}

2.2 BST树中最大结点和最小结点

T& _Max(bstNode<T>* pos);

T& _Min(bstNode<T>* pos);

代码如下：

template<typename T>
T bstTree<T>::Max()
{
	assert(root_);
	bstNode<T>* cur = root_;
	while (cur->right_)
		cur = cur->right_;

	return cur->val_;
}

template<typename T>
T bstTree<T>::Min()
{
	assert(root_);
	bstNode<T>* cur = root_;
	while (cur->left_)
		cur = cur->left_;

	return cur->val_;
}

2.3 BST树的插入方法

bool _Insert(bstNode<T>*& pos,const T& value);

递归实现

template<typename T>
bool bstTree<T>::_Insert(bstNode<T>*& pos, const T& value)
{
	if (pos == nullptr)
	{
		pos = new bstNode<T>(value);
		return true;
	}

	if (pos->data_ > pos)
		_Insert(pos->left_, value);
	else if (pos->data_ < pos)
		_Insert(pos->right_, value);

	return false;
}

非递归实现

template<typename T>
bool bstTree<T>::_Insert(bstNode<T>*& pos, const T& value)
{
	bstNode<T>* cur = pos;
	bstNode<T>* parent = nullptr;

	while (cur)
	{
		parent = cur;
		if (cur->val_ == value)
			return false;
		if (cur->val_ < value)
			cur = cur->right_;
		else
			cur = cur->left_;
	}

	cur = new bstNode<T>(value);
	if (parent == nullptr)
		pos = cur;
	else
	{
		if (parent->val_ > value)
			parent->left_ = cur;
		else
			parent->right_ = cur;
	}

	return true;

}

2.4 BST树的删除方法

bool _Remove(bstTree<T>*& pos,const T& value);

递归实现

template<typename T>
bool bstTree<T>::_Remove(bstTree<T>*& pos,const T& value)
{
	if (pos == nullptr)
		return false;
	else if (pos->val_ < value)
		return _Remove(pos->right_, value);
	else if (pos->data_ > value)
		return _Remove(pos->left_, value);
	else
	{
		if (pos->left_ && pos->right_)
		{
			auto tmp = pos->left_;
			while (tmp->right_ != nullptr)
				tmp = tmp->right_;
			pos->val_ = tmp->val_;
			_Remove(pos->left_, pos->val_);
		}
		else
		{
			auto tmp = pos;
			if (pos->left_ != nullptr)
				pos = pos->left_;
			else
				pos = pos->right_;

			delete tmp;
			return true;
		}
	}
}

非递归实现

template<typename T>
bool bstTree<T>::_Remove(bstTree<T>*& pos,const T& value)
{
	if (pos == nullptr)
		return false;
	bstNode<T>* cur = pos;
	bstNode<T>* parent = nullptr;
	while (cur != nullptr && cur->val_ != value)
	{
		parent = cur;
		if (cur->val_ > value)
			cur = cur->left_;
		else
			cur = cur->right_;
	}

	if (cur == nullptr)
		return false;

	bstNode<T>* tmp;

	if (cur->left_ && cur->right_)
	{
		parent = cur;

		tmp = cur->left_;

		while (tmp->right_)
		{
			parent = tmp;
			tmp = tmp->right_;
		}

		cur->val_ = tmp->val_;

		cur = tmp;
	}

	if (cur->left_ == nullptr && cur->right_ == nullptr)
	{
		if (parent->val_ > cur->val_)
			parent->left_ = nullptr;
		else
			parent->right_ = nullptr;
		delete cur;
		return true;
	}

	if (cur->left_ != nullptr)
		tmp = cur->left_;
	else
		tmp = cur->right_;

	if (parent == nullptr)
	{
		delete pos;
		pos = nullptr;
		return true;
	}

	if (parent->val_ > tmp->val_)
		parent->left_ = tmp;
	else
		parent->right_ = tmp;

	delete cur;
	return true;
}