重学数据结构栈与队列

Posted 2021-08-08 adventure.Li

一、基本框架

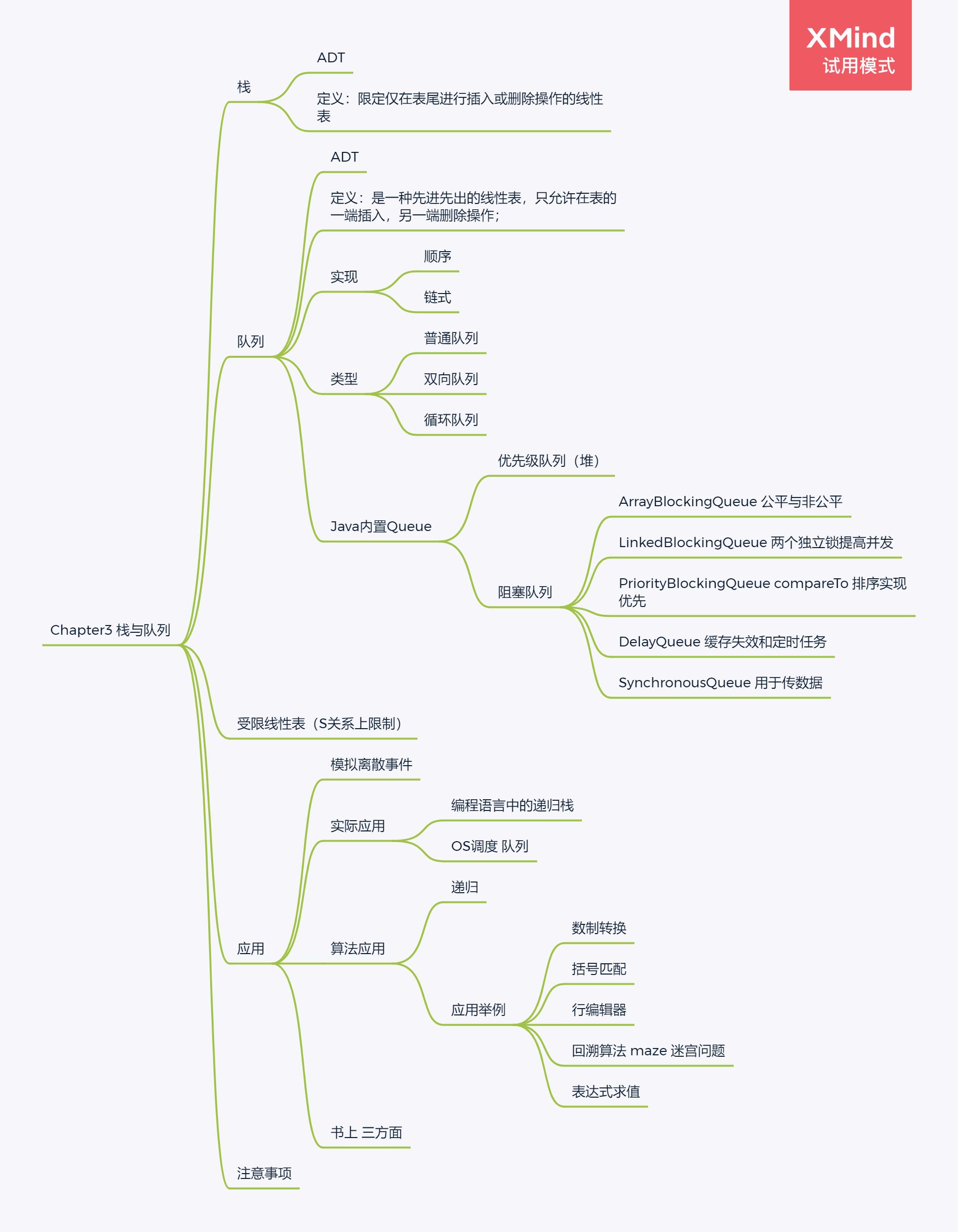
二、基础代码实现

1. Stack

（1）基本概念

Stack的定义：只允许尾部插入或删除操作的线性表。
PS：
堆栈是一个特定的存储区或寄存器，它的一端是固定的，另一端是浮动的 。堆这个存储区存入的数据，是一种特殊的数据结构。所有的数据存入或取出，只能在浮动的一端（称栈顶）进行，严格按照“先进后出”的原则存取，位于其中间的元素，必须在其栈上部（后进栈者）诸元素逐个移出后才能取出。在内存储器（随机存储器）中开辟一个区域作为堆栈，叫软件堆栈；用寄存器构成的堆栈，叫硬件堆栈。

（2）基本操作

template <class Type> class Stack {	
public:
     Stack ( int sz = 10 );	    //构造函数
     void Push (Type x);           //进栈
     int Pop (Type& x);            //出栈
     int GetTop (Type& x);      //取栈顶元素
     void MakeEmpty ( );          //置空栈
     int IsEmpty ( ) const;         //判栈空否
     int IsFull ( ) const;             //判栈满否
}

顺序表实现：

//
// Created by LYF on 2021/7/7.
//
//C++模板类实现编译错误： Error:undefined reference to
//https://blog.csdn.net/Cold_Sun_/article/details/100584418
#ifndef CBASE_SEQSTACK_H
#define CBASE_SEQSTACK_H

template<class T>
class SeqStack {
public:
    SeqStack(int size=10);//Init
    void MakeEmpty();
    bool IsEmpty();
    int GetLength();
    T GetTop();
    void Push(T e);//add a element
    void Pop();//delete the element of top
private:
    T *element;
    int Max_Size=10;
    int base=0,top=0;//栈底,栈顶指针
};

template <class T> //<T>
bool SeqStack<T>::IsEmpty() {
    return top-base==0? true:false;
}

template <class T> //<T>
SeqStack<T>::SeqStack(int size) {
    element=new T[size];
}

// 获取栈顶元素
template<class T>
T SeqStack<T>::GetTop() {
//    if(top==base)
//        return;// 为空
    return element[top-1];
}

// 压栈
template<class T>
void SeqStack<T>::Push(T e) {//<T>
    element[top++]=e;
    if(top>Max_Size-1){
        // C的写法
        element=(T *)realloc(element,10);
        Max_Size+=10;//扩容
    }
}

//
template<class T>
void SeqStack<T>::Pop() {//<T>
    if(top==base)
        return;//为空
    top--;
    //free(element[top--]);//数组是连续的内存，不能中间拿掉某一块。
}

template<class T>
int SeqStack<T>::GetLength() {//<T>
    return top - base;
}
#endif //CBASE_SEQSTACK_H

简单测试：

// 实现栈的基本操作检测
void BaseFunTest(){
    SeqStack<int> stack;//<int>
    for(int i=0;i<12;i++)
    {
        int val = rand()%50+1;
        cout<<"random push val:"<<val<<endl;
        stack.Push(val);
    }
    cout<<"get the attributes of the stack"<<endl;
    cout<<"len:"<<stack.GetLength()<<"top:"<<stack.GetTop()<<endl;
}

Java版：

栈的实现，既可以链表，也可以顺序实现；而Java中源码采用extends（拓展）vector（基于数组存储数据）实现，具有扩容机制。

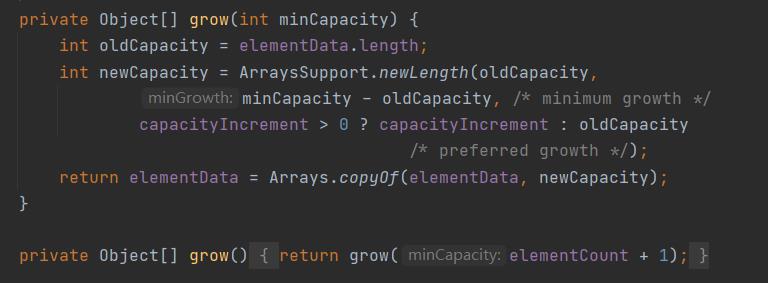
（3）JVM中的堆栈

JVM是运行在OS之上的虚拟计算机，分为 运行数据部分 方法区、堆栈等，其中栈主要用于存储数据基本类型和引用，在函数调用方面起到了重要实现。

（4）算法应用

栈：在算法中应用实际思维层面并不难，但可能比较繁琐（比如说表达式求值，需要处理字符串到数值的转换问题）。主要好处是进行逆置回退（而回退是递归中重要部分，也是回溯算法或者深搜穷举的关键步骤，）
队列：应用主要在调度处理作业队列，以及消息中间件（生产者、消费者问题）。进行存储转发、阻塞。

1. 数制转换

// 1.进制转换问题
int ScaleChange(int n,int scale)
{
    SeqStack<int> s;
    while(n){
        s.Push(n%scale);
        n/=scale;
    }
    cout<<"rs:"<<endl;
    while(!s.IsEmpty()){
        cout<<s.GetTop();
        s.Pop();
    }
    return 1;
}

（2）括号匹配

// 2.括号匹配问题
// 思路: stack进行存储字符,当出现匹配的符号就消掉，直到最后，若栈为空则符号否则不符合
void IsRight(){
    string str;
    cout<<"Please enter strings:"<<endl;// (())[]{}
    int i=0;
    while(i++<10){
        getline(cin,str);
        cout<<str<<endl;
        SeqStack<char> stack;
        for(int i=0;i<str.length();i++){
            if(stack.IsEmpty()){
                stack.Push(str[i]);
            }else{
                // 判断
                char tmp =stack.GetTop();
                if(tmp==')'||tmp==']'||tmp=='}'){
                    cout<<"Not Right"<<endl;
                    break;
                    //return false;
                }else{
                    switch (tmp) {
                        case '(': if(str[i]!=')')stack.Push(str[i]);else stack.Pop();break;
                        case '[': if(str[i]!=']')stack.Push(str[i]);else stack.Pop();break;
                        case '{': if(str[i]!='}')stack.Push(str[i]);else stack.Pop();break;
                    }
//                    stack.Pop();//另外可以进行打表记录,优先级问题
                }
            }
        }


        if(stack.IsEmpty()){
            cout<<"Right!"<<endl;
        }else{
            cout<<"Not Right!"<<endl;
        }
    }
}

（3）迷宫问题（）BFS

// 5.利用栈实现迷宫BFS问题
#define size 8
int maze[size][size]={
    0,1,1,1,1,1,0,0,
    0,0,0,1,1,1,0,0,
    0,1,0,1,1,1,0,0,
    1,1,0,0,1,0,0,0,
    0,1,1,0,1,0,1,0,
    0,1,1,0,0,0,1,0,
    0,1,1,1,1,1,0,0,
    0,1,1,1,1,1,0,0
};
int dir[2][4] ={
        {1,0,-1,0},
        {0,1,0,-1}
};
struct node{
    node *pro;//前驱节点
    int level;
    int x,y;
};

// BFS
void mazeProblem(){
    SeqStack<node*> stack;
    node *first;
    first = (node*)malloc(sizeof(node));
    first->pro=NULL;
    first->y=0;
    first->x=0;
    first->level=1;
    stack.Push(first);// 加入起点进行搜索
    int pathLen = 0;// 计算深度（树的），路径即树的路径
    while(!stack.IsEmpty())// 非空就进行搜索
    {
        // 取出一点
        node *tmp = stack.GetTop();
        stack.Pop();
        maze[tmp->y][tmp->x]=1;
        pathLen++;
        if(tmp->y==size-1&&tmp->x==size-1){// 出口
            cout<<"can arrive path is len:"<<tmp->level<<tmp->x<<":"<<tmp->y<<endl;// 通过前驱打印
            node *p = tmp;
            while(p!=NULL){
                cout<<p->y<<";"<<p->x<<endl;
                p=p->pro;
            }
            return;
        }

        // 四个方向进行搜索
        for(int i=0;i<4;i++){
            int tmpX = tmp->x+dir[0][i];
            int tmpY = tmp->y+dir[1][i];
            if(tmpX>=0&&tmpX<size&&tmpY>=0&&tmpY<size&&maze[tmpY][tmpX]!=1){
                node *newNode;
                newNode = (node*)malloc(sizeof(node));//指针就需要内存分配
                newNode->pro = tmp;
                // 内存分配考虑？
                newNode->level=tmp->level+1;
                newNode->x = tmpX;
                newNode->y = tmpY;
                maze[tmpY][tmpX]=1;
                stack.Push(newNode);//加入符合要求的节点（坐标点），
            }
        }
    }
    cout<<"cant arrive !"<<endl;
}