《数据结构与算法》---(哔哩哔哩--王卓老师笔记)史上最详细笔记
Posted 闲言_
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《数据结构与算法》---(哔哩哔哩--王卓老师笔记)史上最详细笔记相关的知识,希望对你有一定的参考价值。
视频地址:
前言
“程序=数据结构+算法”
1.、数据结构基本概念
1.1 数据结构研究内容
通过用计算机解题一个问题的步骤
- 具体问题抽象为数学模型(实质:分析问题、提取操作对象、找出操作对象之间的关系、用数学语言描述) =》数据结构
- 设计算法
- 编程、调式、运行
早期,计算机主要用于数值计算
数据结构出现领域
- 线性结构:图书管理系统、人事管理系统、仓库管理系统、通讯录
- 树形结构:人机对弈、文件系统的系统结构
- 图(网状结构):地图信息处理
1.2 数据、数据元素、数据项和数据对象
1.3 数据结构
1.4 数据类型和抽象数据类型
-
在使用高级程序设计语言编写程序时,必须对程序中出现的每个变量、常量或表达式,明确说明它们所属的数据类型
-
一些最基本数据结构可以用数据类型来实现,如数组、字符串等
-
而另一些常用的数据结构,如栈、队列、树、图,不能直接用数据类型来表示,
。 -
高级语言中的数据类型明显的或者隐含地规定了在程序执行期间变量和表达式的所有可能的取值范围,以及在这些数值范围上所运行进行的操作。
数据类型的作用
- 约束常量或变量的取值范围
- 约束常量或变量的操作。
(1)什么是数据类型?
- 数量类型是一组性质相同的值得集合以及定义于这个值集合上的一组操作的总称。
(2)什么是抽象数据类型?
是指一个数学模型以及定义在此数学模型上的一组操作
-
由用户定义,从问题抽象出数据模型(逻辑结构)
-
还包括定义在数据模型上的一组抽象运算(相关操作)
-
圆:到某个点的距离相等的点的集合
-
运算:构造圆、求面积、求周长
抽象数据类型的形式定义 -
抽象数据类型可用(D,S,P)三元组表示
-
其中:D是数据对象;
-
S 是D上的关系集
-
P是对D的基本操作集
1.5算法与算法分析
对特定问题求解方法和步骤的一种描述,它是指令的有限序列。其中每个指令表示一个或多个操作。
简而言之,算法就是解决问题的方法和步骤
1.5.1算法描述
(1)自然语言:英语、中文
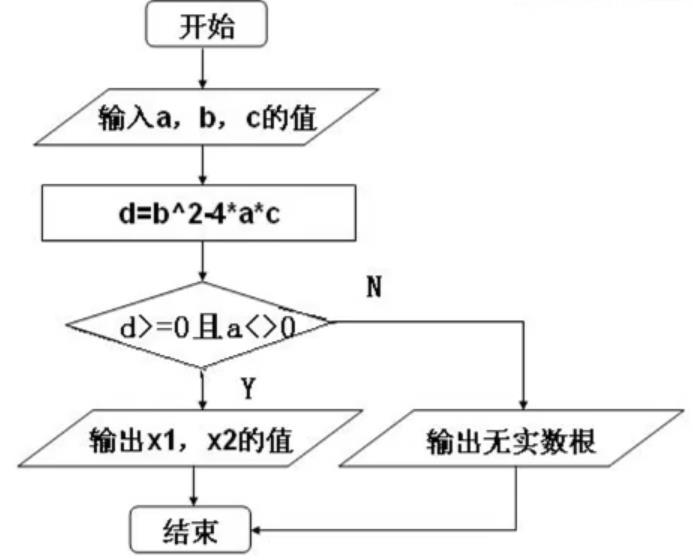
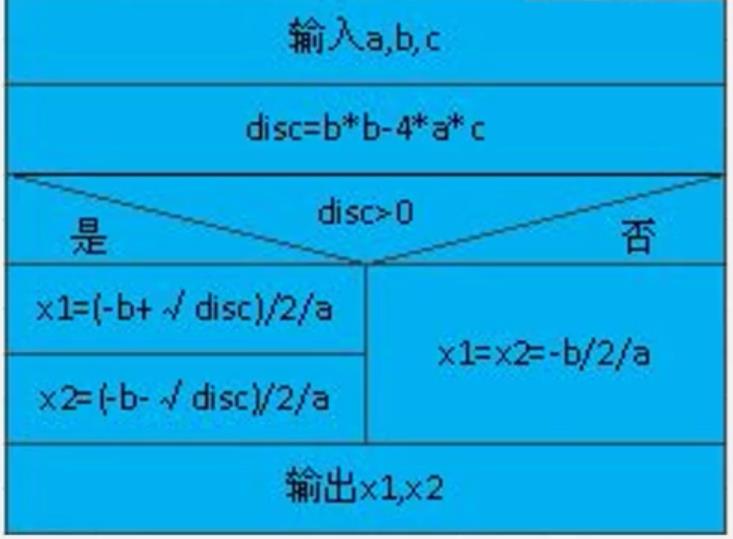
(2)流程图:传统流程图、NS流程图
(3)类语言:类C语言
(4)C语言程序、JAVA语言程序

1.5.2算法描述
算法是解决问题的一种方法或一个过程,考虑如何将输入转换成输出,一个问题可以有多种算法。
程序是用某种程序设计语言的具体实现
程序=数据结构+算法
- 数据结构是通过算法实现操作
- 算法根据数据结构设计程序
1.5.3算法特性
一个算法必须具备以下五个重要特性
- 有穷性:一个算法必须总是在执行又穷之后结束,其每一步都在又穷时间内容完成
- 确定性:算法中的每一条指令都必须有确切的含义,每一二义性,在任何条件下,只有唯一的一条执行路径,即对于相同的输入只能得到相同的输出
- 可行性:算法是可执行的,算法描述的操作可以通过已经实现的基本操作执行有限次来实现
- 输入:一个算法有零个或多个输入
- 输出:一个算法有一个或多个输出
1.5.4算法设计的要求
- 正确性
- 可读性
- 健壮性
- 高效性
一个好的算法首先具备正确性,然后是健壮性,可读性,在几个方面都满足的情况下,主要考虑算法的效率,通过算法的效率高低俩评判不同算法的优劣程度。:
1.时间效率:指的是算法所耗的时间;
2.空间效率:指的是算法执行过程中所耗费的存储空间
时间效率和空间效率有时候是矛盾的。
算法时间效率的度量
- 算法时间效率可以依据该算法编制的程序在计算机上执行所消耗的时间来度量
- 两种度量方法
- (1)事后统计:将算法实现,测算其时间和空间开销。
- (2)事前分析:对算法所消耗资源的一种估算方法。
1.5.5算法时间复杂度
- 最坏时间复杂度:指在最坏情况下,算法的时间复杂度
- 平均时间复杂度:指在所有可能输入实例在等概率出现的情况下,算法的期望运行时间。
- 最好时间复杂度:指在最好情况下,算法的时间复杂度
- 通常只考虑:只考虑最坏和平均时间复杂度。
怎么求算法的时间复杂度?
第一步找出来执行次数最多的语句,怎么找?找嵌套层次最深的。
有的情况下,算法中的基本操作重复执行的次数还随问题的输入数据集不同而不同
1.5.6算法空间复杂度
空间复杂度:算法所需存储空间的度量,
记做:S(n)=O(f(n))
其中n为问题的规模(或大小)
- 算法要占据的空间
- 算法本身要占据的空间,输入\\输出,指令,常量,变量等
- 算法要使用的辅助空间
【例】将一维数组a中的n个数逆序存放到原数值中。
- 算法1(通过临时变量)
- 用了一个变量的空间
- 原地工作
public class Test1{
public static void main(String[] args) {
int[] a = {3, 2, 5, 42, 67, 8, 10};
parintArray(a);
int[] arr = arr(a, 7);
parintArray(a);
}
/**
* 交换方法
*
* @param a
* @param n
* @return
*/
public static int[] arr(int[] a, int n) {
int t;//额外空间
for (int i = 0; i < n / 2; i++) {
//第一个和最后一个进行交换
//交换元素
//交换n次
t = a[i];
a[i] = a[n - i - 1];
a[n - i - 1] = t;
}
return a;
}
/**
* 打印数组
*
* @param a
*/
public static void parintArray(int[] a) {
String arr = "[";
for (int i = 0; i < a.length; i++) {
if (i == a.length - 1) {
arr += a[i] + "]";
} else {
arr += a[i] + ",";
}
}
System.out.println(arr);
}
}
- 算法2(通过临时数组)
- 辅助数组b
public class Test1{
public static void main(String[] args) {
int[] a = {3, 2, 5, 42, 67, 8, 10};
parintArray(a);
int[] arr = arrTwo(a, 7);
parintArray(a);
}
/**
* 交换方法
*
* @param a
* @param n
* @return
*/
public static int[] arrTwo(int[] a, int n) {
//定义b数组
int[] b = new int[a.length];
//将数组a的数据倒数存储到b数组总
for (int i = 0; i < n; i++)
b[i] = a[n - i - 1];
//将b数组的数据存储到a数组中
for (int i = 0; i < n; i++)
a[i] = b[i];
return a;
}
/**
* 打印数组
*
* @param a
*/
public static void parintArray(int[] a) {
String arr = "[";
for (int i = 0; i < a.length; i++) {
if (i == a.length - 1) {
arr += a[i] + "]";
} else {
arr += a[i] + ",";
}
}
System.out.println(arr);
}
}
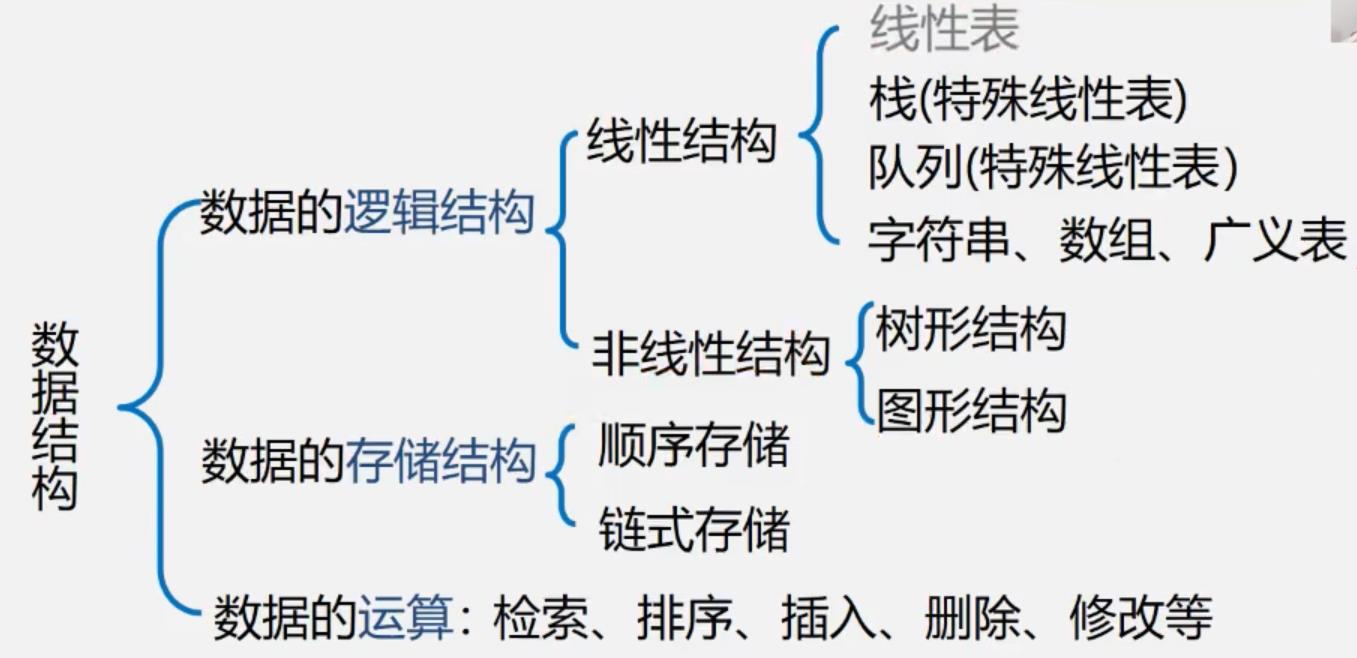
2.、基本的数据结构
2.1、线性结构
2.1.1线性表
(1)线性表的定义和特点
线性表是具有相同特性的数据元素的一个有限序列
(a1,a2,a3,a4...an)
第一个元素称为:线性起点
最后一个元素称为:线性终点
下标,是元素的序号,表示元素在表中的位置
线性表(Liner List):
由n(n>=0)个数据元素(节点)a1,a2,a3…an组成的有限序列。
- 其中数据元素的个数n定义为表的长度
- 当n=0时称为空表
- 将非空的线性表(n>0)记住:(a1,a2,…an)
- 这里的数据元素ai(1<=i<=n)只是一个抽象符合,其具体含义在不同的情况下可以不同
例1:分析由26个英文字母组成的英文表
{A,B,C,D…Z}
数据元素都是字母;元素间关系是线性
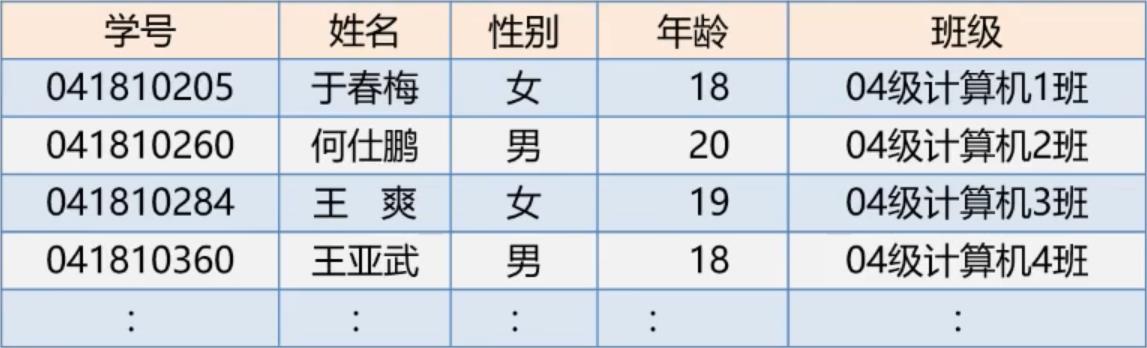
例2:分析学生情况登记表
学号、姓名、性别、年龄、班级,一个数据元素就是一个学生的记录。若干个学生的关系就是一个线性关系
从上面例子可看出线性表的逻辑特征:
- 在非空的线性表,有且仅有一个开始结点a1,它没有直接前驱,而仅有一个直接后继a2;
- 有且仅有一个终端结点an,它没有直接后继,而仅有一个直接前驱an-1
- 其余内部结点ai(2<=i<=n-1)都有且仅有一个直接前驱ai-1和一个直接后继ai+i。
线性表示一种典型的线性结构
总结:同一线性表中的元素必定具有相同特性,数据元素间的关系是线性关系
(2)案例引入
例1:一元多项式的运算:实现两个多项式加,减,乘运算
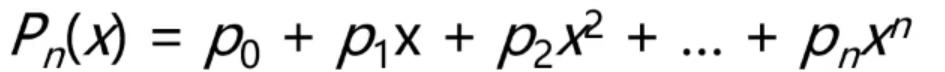
线性表P={P0,P1,P2,…,Pn}
(每一项的指数i隐含在其系数pi的序号中)
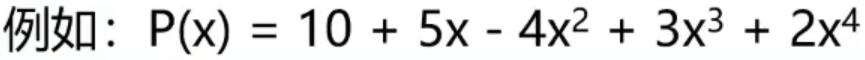
用数组来表示
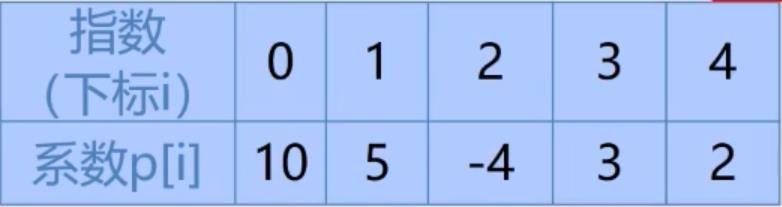
只需要把两个多项式当中的元素,下标为xx的元素与常系数相加接口。
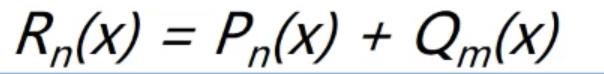
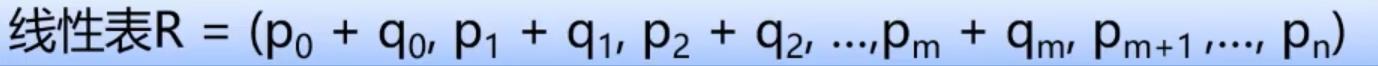
例2:图书信息管理系统
功能需求:
- 查询
- 插入
- 删除
- 修改
- 排序
- 计数
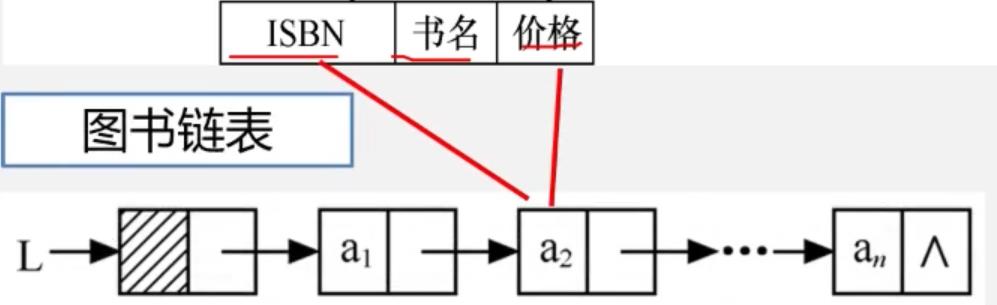
图书表抽象为线性表
表中每本图书抽象线性表中的数据元素
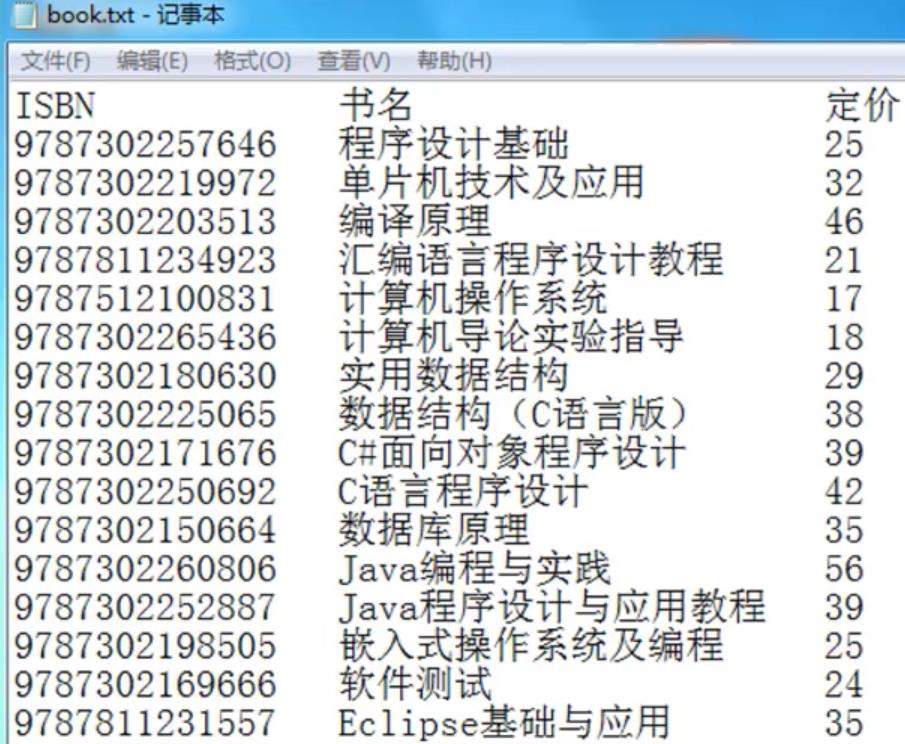
使用数组存储
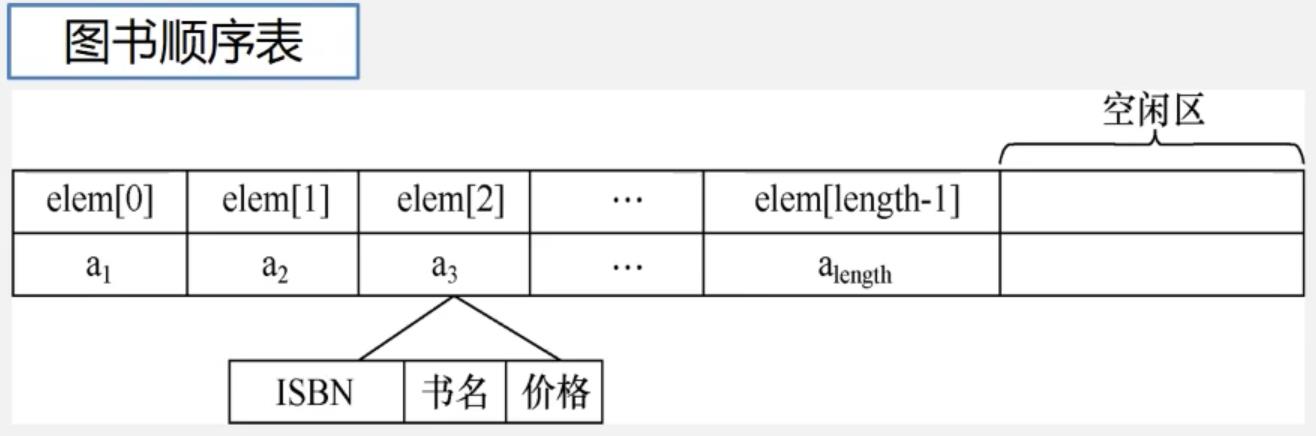
使用链表存储
选择适当的存储结构
实现此存储上的基本操作
利用基本操作完成功能
比较这两种存储方式
总结:
线性表中数据元素的类型可以为 简单类型,也可以为 复杂类型。
许多实际应用问题所涉及的基本操作有很大相似性,不应为每个具体应用单独编写一个程序。
从具体应用中抽象出共性的 逻辑结构和基本操作(抽象数据类型),然后实现其 存储结构和基本操作
(3)线性表类型定义
(4)线性表的顺序表示和实现
(5)线性表的链式表示和实现
(6)顺序表和链表的比较
(7)线性表的应用
(8)案例分析与实现
2.1.2栈和队列
2.1.3串
2.1.4数组和广义表
2.2、非线性结构
(1)树
(2)图
3、基本的数据处理技术
3.2、查找技术
3.2、排序技术
以上是关于《数据结构与算法》---(哔哩哔哩--王卓老师笔记)史上最详细笔记的主要内容,如果未能解决你的问题,请参考以下文章