CF 1529D Kavi on Pairing Duty

Posted 2021-08-08 Jozky86

CF 1529D Kavi on Pairing Duty

题意：

有2 * n个点，现在要求两个点连成线段，每个连法都可以得到n个线段，合法的连接方式为：连接的n个线段，任意两个线段要么长度相等，要么有包含关系
n<=1e6

题解：

思维题+推公式
我们设dp[n]:表示2 * n点时合法的线段个数
题目有两个限制条件，我们先考虑第一个：
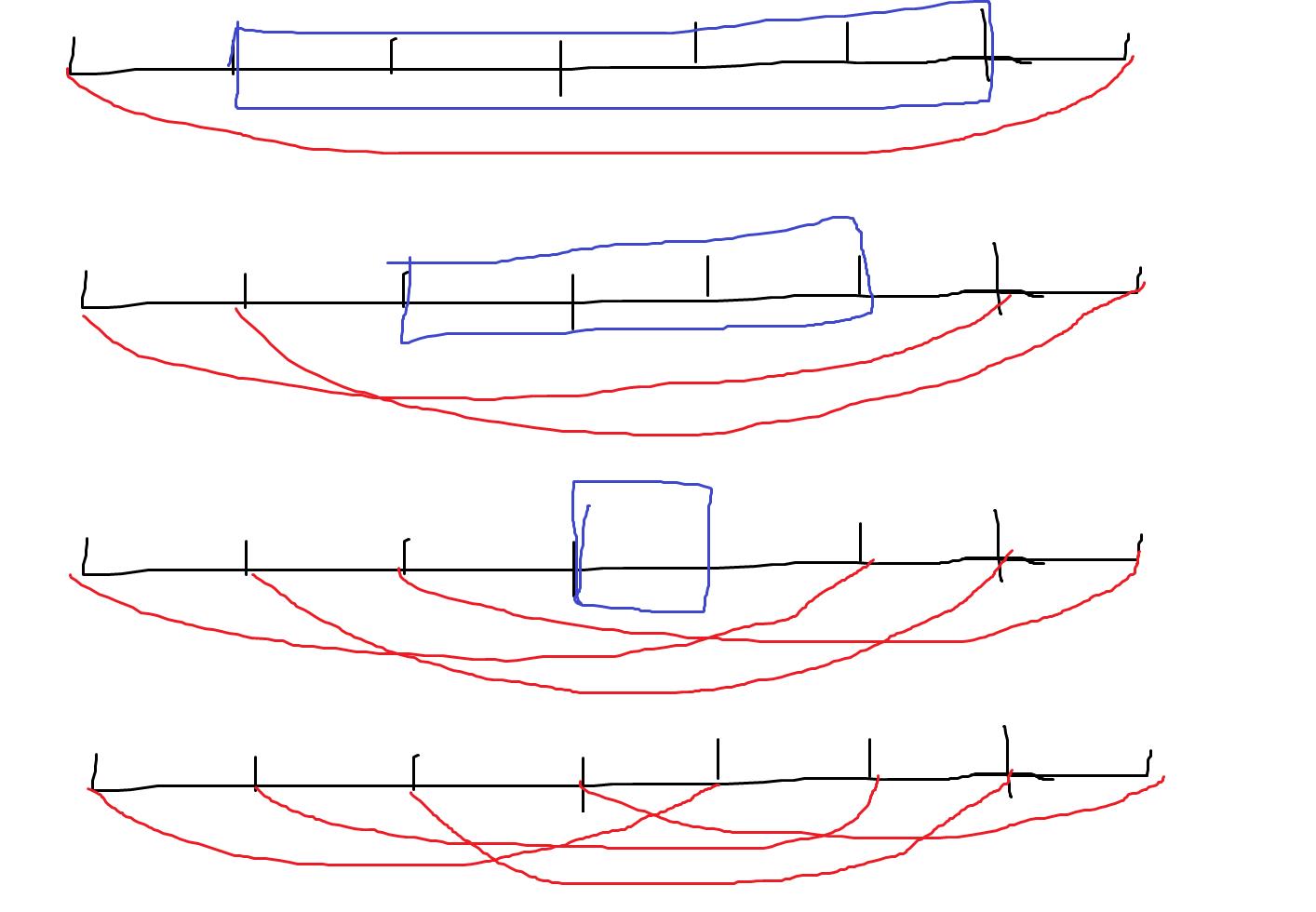
如果有包含关系的话：
如图

1. 连接点1和点2n，得到线段(1,2n)，此时剩下2n-2个点都在这个线段之下，而中2n-2个点的组合与外面这个线段无关，不正是dp[n-1]吗，所以方案数就是 1 * dp[n-1]
2. 连接线段(1,2n-1),(2,2n),此时剩下2n-4个点在这两个线段之下，同上，方案数为dp[n-2]，
3. 以此类推可以得到：存在线段包含的情况下有Σ_i=0^n-1dp[i]
   
   我们考虑所有线段都相等的情况(此时不存在线段包含)：
   如图，图中为n=4的线段都相等不存在包含的情况：
   

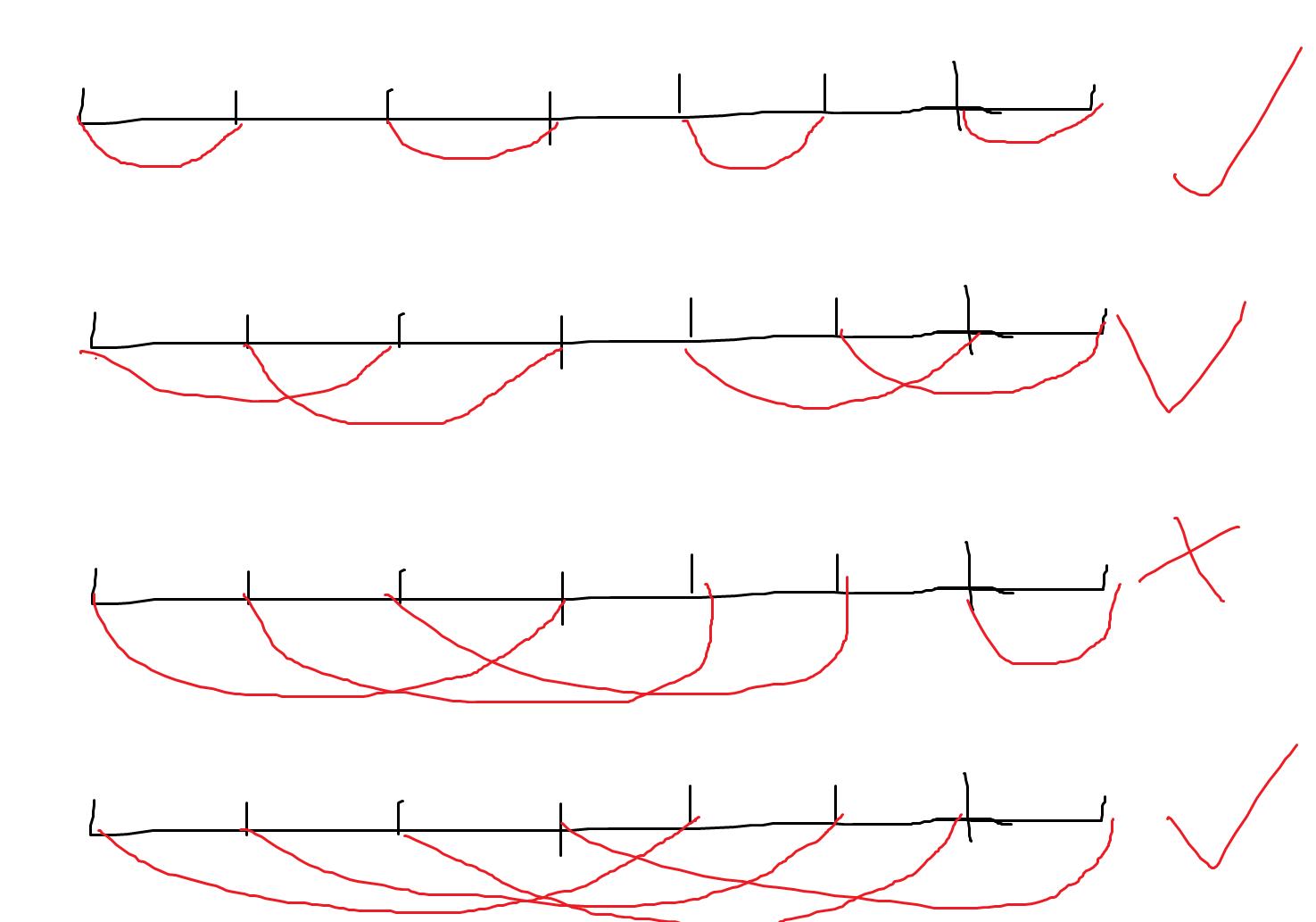
第一个为长度为1，第二个为长度为2，第三个为长度为3，第四个为长度为4，如果再长就超出去了，我们发现第三个是不合法的，通过举例观察就会发现，只有当长度为n的因子时，才是合法的，因为只有因子才能够分配均匀。所以这种情况答案就是n的因子个数，但是这样并不完全对，我们看第二个图的最后一个情况，和第一个图的最后一个情况竟然是一样的，出现了重复，为了去重，所以我们定义第二个情况的答案为n的因子个数-1
约数个数可以用线性筛求，直接求会超时(n最大到1e6)
最终答案为两者相加：

dp[0]=1

代码：

#include<bits/stdc++.h>
#define debug(a,b) printf("%s = %d\\n",a,b);
typedef long long ll;
using namespace std;

inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();//s=(s<<3)+(s<<1)+(ch^48);
   return s*w;
}
const int maxn=1e6+9;
const int mod=998244353;
ll siz[maxn];
ll dp[maxn];
ll sum[maxn];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){//fac[i]表示i的因子的个数 
		for(int j=i;j<=n;j+=i)
		{
			siz[j]=(siz[j]+1)%mod;
		}
	}
	dp[0]=1; 
	sum[0]=1;//sum[i]=a[0]+...+a[i]
	for(int i=1;i<=n;i++){
		dp[i]=(sum[i-1]+siz[i]-1)%mod;
		sum[i]=(sum[i-1]+dp[i])%mod;
	}
	cout<<dp[n];
}