图论基本概念及存储结构遍历方式
Posted 踩踩踩从踩
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图论基本概念及存储结构遍历方式相关的知识,希望对你有一定的参考价值。
前言
图论是数学中的概念,但应用在数据结构与算法学中相当重要的;应用在交通网络中,以及人工智能这些,任务分配的思想,都需要以图为基础,因此研究图论也是非常重要的,本篇文章主要介绍图论一些基本概念、基本性质、存储结构、以及遍历方式、为深层次研究图论打下一个基础。
概念
图是什么,我们需要下个定义,我们从数据结构与算法中可以知道:
图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为 G (V,E) 其中 G 表示一个图
V表示图G中顶点的集合 E表示图G中边的集合
从上面概念来看图是不可能存在空图的,因为至少需要一个顶点但是他们可以没有边,这就是图

以上面图的概念分析 出一个应用,例如两省之间的高速铁路,将两个省进行连接,当然实际生活中两个省之间肯定不只是一条高速铁路,我们用图就能表示两个省之间连接
我们怎么通过河南,以最快的方式达到贵州 这就是图论的应用,是不是感觉生活中就太多应用了,特别是地图这面,我相信各位对图论有个大的概念了,所有与路径有关的都可以用图论解决
图的基本概念
无向图
也就是说边是无向的,若顶点vi到vj之间没有方向,则称这条边为无向边(edge),用无序偶对(vivj)来表示,如果图中任意两个顶点之间的边都是无向边,则称该图为无向图

如上图所表示的,任意两个顶点之间的边都是无向边就是无向图,没有方向的指向;并且 任意两个顶点之间都存在边,则称该图为无向完全图
有向图
依据上面的无向图,推论出,如果两个顶点的边为有向,则为有向图,用有序偶<vi,vj> 来表示,vi称为弧尾,vj称为弧头 ,在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称为有向完全图

图的权
普通两个顶点之间,一般会带入某个信息的,比如距离的长度,向这样的数就是图的权重,这些在

连通图
在无向图中,如果v到v1有路径,则v和v1是连通的,如果对于任意两个顶点都连通,则称为连通图,如果说这样的算法,让我想到了撒,我会想到java虚拟机中 判断 是否回收对象的可达性分析算法,gcroot引用的对象

无向图和有向图,平常我们研究的就是连通图
度
无向图顶点的边数叫度,有向图顶点的边数叫出度和入度;这和树中的度很像,一个顶点上边的集合
对于无向图则
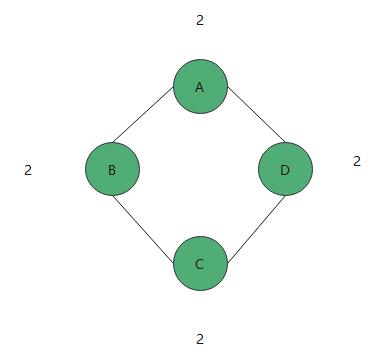
对于有向图的度,则分为入度和出度,这些基本概念我相信大家都明白,我就不画图看了
图的数据存储结构
也正是犹豫图的结构比较复杂,任意两个顶点之间都可能存在联系,因此无法以数据元素在内存中的物理位置来表示元素之间的关系,也就是说图不能用简单的顺序存储结构来表示 ,各种方式
邻接矩阵
考虑到图是由顶点和边或弧两部分组成,合在一起比较困难,那很自然就分两个结构来分别存储,顶点不分大小,主次,所以用一个一维数组来存储;而边或弧是顶点与顶点之间的关系,一维搞不定,那就用二维数组来存储,于是邻接矩阵就是出现了,就是二维数组
图的邻接矩阵存储方式是用两个数组来表示图,一个一维数组存储图中顶点信息,一个二维数组存储图中边的信息
具体的 有向图和无向图,带权的图又是怎么存储的,我们在来看一下
无向图
设图G有n个顶点,则邻接矩阵是一个nxn的方阵,定义为

来看一个实例

上面的无向图用邻接矩阵表示就可以用下面的

这样画的二维数组看起来和数学的还是不太一样 ,大概就是下面一部分的

无向矩阵的边数组是一个对称矩阵
从横向就能算到一个顶点的度,我们是不是直观的体验了
有向图
我们在看有向图,和无向图的存储方式也是一样的,加了方向之后,对于表示方式有一点点不一样,顶点之间有入度和出度的关系,


然后我们在来看看通过二维数组来表示

这是不是一目了然,大家明白树和图论的两种数据结构的表示方式, 图论需要表示出路径,并计算出每个顶点到另一个顶点的路径 最优路径等等

通过邻接矩阵来表示,这其中还有个概念就是顶点的入度和出度的,从横向来看某个顶点的出度,而竖向节点就是顶点的出度,这是根据我们邻接矩阵的存储方式决定的
带权有向图
带权的有向图,是整合了既有方向 又有权重的图,就是带权有向图,比较麻烦的一种图论。
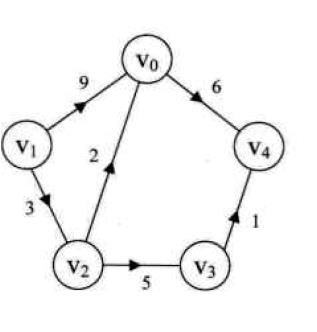
从上面的图,怎么样来表示, 我想大家应该能想到怎么来表示了把,主要是把有向图中的1改变成具体的权重,然后在通过很大的数来表示无法走到 ,相同的顶点则采用0表示,这个我们在继续看图来说明

具体代码实现
首先先把需要的属性给定义好
public int[] vertices;//顶点集
public int[][] matrix;//图的边的信息
public int verticesSize;
public static final int MAX_WEIGHT = Integer.MAX_VALUE;
从上面的带权重的有向图中
- 包括顶点数组(vertices) 以及边的二维数组(matrix),
- 还有需要顶点集合的大小(verticesSize),计算出边的大小
- 当然我们对于无法到达情况的边,定义特殊的值(MAX_WEIGHT)
建立构造方法, 将所有的数组进行初始化,并赋值,为了简单因此还是直接用的i赋值赋值代替顶点
public Graph(int verticesSize) {
this.verticesSize = verticesSize;
vertices = new int[verticesSize];
matrix = new int[verticesSize][verticesSize];
for (int i = 0; i < verticesSize; i++) {
vertices[i] = i;
}
}然后写一些需要计算的方法,包括
- 计算v1到v2的权重, 如果是无穷大,则返回-1,表示这个v1无法直接到达v2 或者无法到达顶点
/**
* 计算v1到v2的权重(路径长度)
*/
public int getWeight(int v1, int v2) {
int weight = matrix[v1][v2];
return weight == 0 ? 0 : (weight == MAX_WEIGHT ? -1 : weight);
}- 获取顶点,则直接返回顶点集就行
/**
* 获取顶点
*/
public int[] getVertices() {
return vertices;
}- 获取入度, 遍历数组 的竖向,带权重的进行相加即可 也就是下面的 图的表示 获取出度,遍历数组 的竖向,带权重的进行相加即可

/**
* 获取出度
*/
public int getOutDegree(int v) {
int count = 0;
for (int i = 0; i < verticesSize; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != MAX_WEIGHT) {
count++;
}
}
return count;
}
/**
* 获取入度
*/
public int getInDegree(int v) {
int count = 0;
for (int i = 0; i < verticesSize; i++) {
if (matrix[i][v] != 0 && matrix[i][v] != MAX_WEIGHT) {
count++;
}
}
return count;
}上面是代码的实现,如果用邻接矩阵来表示 ,直接构造出边数组
Graph graph = new Graph(5);
int[] v0 = new int[]{0, 1, 1, MAX_WEIGHT, MAX_WEIGHT};
int[] v1 = new int[]{MAX_WEIGHT, 0, MAX_WEIGHT, 1, MAX_WEIGHT};
int[] v2 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 0, MAX_WEIGHT, MAX_WEIGHT};
int[] v3 = new int[]{1, MAX_WEIGHT, MAX_WEIGHT, 0, MAX_WEIGHT};
int[] v4 = new int[]{MAX_WEIGHT, MAX_WEIGHT, 1, MAX_WEIGHT, 0};
graph.matrix[0] = v0;
graph.matrix[1] = v1;
graph.matrix[2] = v2;
graph.matrix[3] = v3;
graph.matrix[4] = v4;最简单的方式构造出邻接矩阵 图
图的遍历
深度优先和广度优先,这是图论中的遍历方式,区别于树种 前中后序遍历 层次遍历的方式
深度优先
深度优先的概念,也叫深度优先搜索,它的遍历规则,不断的沿着顶点的深度方向遍历。顶点的深度方向是指它的邻接点方向。
具体点,给定一图G=<v,e> 用visited[i] 表示顶点i的访问情况,则初始情况下所有的visited为false,假设从顶点V0开始遍历,则下一个遍历的顶点是v0的第一个邻结点v1, 接着遍历第一个邻接点vj,直到所有顶点都被访问过。
所谓第一个是指在某种存储结构中(邻接矩阵 邻接表) ,所有邻结点中存储位置最近的,通常指的是下标最小的,遍历的过程中有两种这样的情况
深度优先的展示
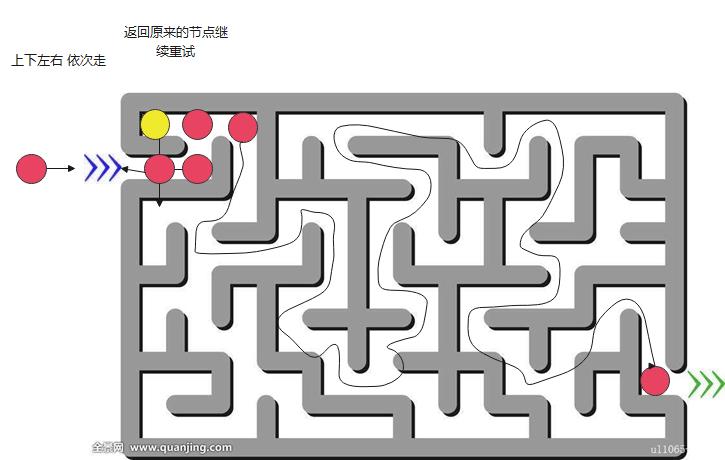
在邻接矩阵中实现


这种方式就是深度优先 ,一旦走到死胡同,就退到上一个地方
代码实现
想想刚才的思路 首先我们先从小的方法去写,
- 需要创建获取第一个邻接点的方法,由小到大的方式 从左往后 寻找就行 ,
/**
* 获取第一个邻接点
*/
public int getFirstNeightBor(int v) {
for (int i = 0; i < verticesSize; i++) {
if (matrix[v][i] > 0 && matrix[v][i] != MAX_WEIGHT) {
return i;
}
}
return -1;
}- 创建获取顶点v的邻结点index的下一个邻结点
/**
* 获取到顶点v的邻接点index的下一个邻接点
*/
public int getNextNeightBor(int v, int index) {
for (int i = index + 1; i < verticesSize; i++) {
if (matrix[v][i] > 0 && matrix[v][i] != MAX_WEIGHT) {
return i;
}
}
return -1;
}接下来我们 写深度优先的算法 这个前序遍历方法就很像了
写深度优先算法时,需要考虑顶点 是否已经到过, 在这里用boolean来做判断
public boolean[] isVisited;
isVisited = new boolean[verticesSize];添加 属性 isvisited 并在 构造方法种初始化 该值
开始深度优先算法
/**
* 深度优先(很象二叉树的前序)
*/
public void dfs() {
for (int i = 0; i < verticesSize; i++) {
if (!isVisited[i]) {
System.out.println("viested vertice " + i);
dfs(i);
}
}
}- 从v0开始 ,这就是深度优先遍历的方法
public void dfs(int i) {
isVisited[i] = true;
int v = getFirstNeightBor(i);
while (v != -1) {
if (!isVisited[v]) {
System.out.println("visted vertice " + v);
dfs(v);
}
v = getNextNeightBor(i, v);
}
}
广度优先
广度优先遍历又叫广度优先搜索,它的遍历规则:
1.先访问当前顶点的所有邻结点。(这就是广度的意思)
2.先访问顶点的邻结点先于后访问顶点的邻接点被访问
给定一图G=<v,e> 用visited[i] 表示顶点i的访问情况,则初始情况下所有的visited为false,假设从顶点V0开始遍历,且顶点v0的邻结点下表从小到大有v1、vj ....vk 按规则1,接着遍历 vi vj 在来应遍历vi的所有的邻结点之后是vj的邻结点 ,这个和树是不是很像

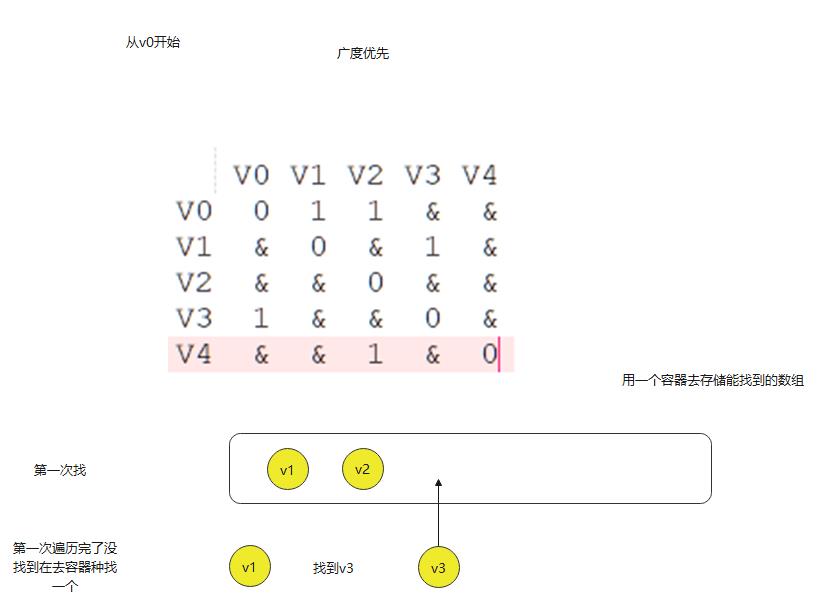
public void bfs(int i) {
LinkedList<Integer> queue = new LinkedList<>();
//找第一个邻接点
int fn = getFirstNeightBor(i);
if (fn == -1) {
return;
}
if (!isVisited[fn]) {
isVisited[fn] = true;
System.out.println("visted vertice:" + fn);
queue.offer(fn);
}
//开始把后面的邻接点都入队
int next = getNextNeightBor(i, fn);
while (next != -1) {
if (!isVisited[next]) {
isVisited[next] = true;
System.out.println("visted vertice:" + next);
queue.offer(next);
}
next = getNextNeightBor(i, next);
}
//从队列中取出来一个,重复之前的操作
while(!queue.isEmpty()){
int point=queue.poll();//v1 v2
bfs(point);
}
}
/**
* 广度优先
*/
public void bfs(){
for (int i = 0; i < verticesSize; i++) {
isVisited[i]=false;
}
for (int i = 0; i < verticesSize; i++) {
if(!isVisited[i]){
isVisited[i]=true;
System.out.println("visited vertice:"+ i);
bfs(i);
}
}
}这就是整个广度优先去查找数据 一层一层的往下走的
图的另外一种存储结构
邻接表
无向图
将具体的连接顶点都创建一个节点进行存储

有向图

将方向和无向图结合起来的方式

带权 有向图
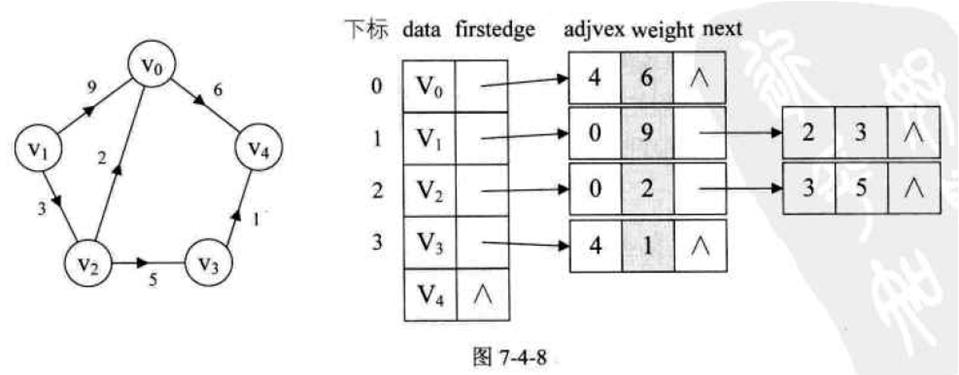
这用链表的方式来表示图论,这个不过多的研究,从后续的博客中我在继续研究
总结
本篇博客是介绍图是什么,用于什么场景,广泛用于生活中,并学习他的遍历思想,比较基础,但是希望各位看了这篇博客,对图有个大的概念,不在陌生。
以上是关于图论基本概念及存储结构遍历方式的主要内容,如果未能解决你的问题,请参考以下文章