[信息论与编码理论专题-6]:物理层信道编码
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[信息论与编码理论专题-6]:物理层信道编码相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/118638025
第1部分 信道编码的基本概念
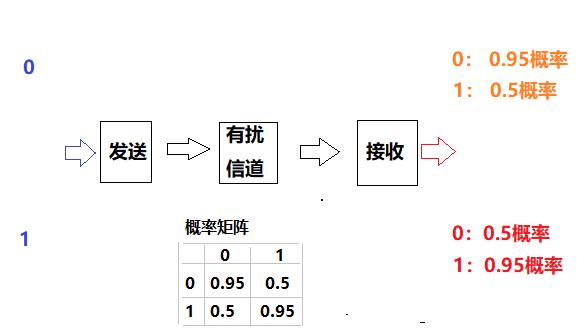
思考:如果收到的数据不可靠,那接收端怎么才能判断收到的数据是0还是1呢?
这就需要信道编码,确保接收方收到的数据确实是发送方发送的数据,而不是受干扰后的数据!


备注:
物理层编码的本质原因是:信道是有扰信道,而不是理想信道。这就导致了单个比特通信时,接收方收到的符号如果是1,并不表明发送方发送的一定是1,有可能是出错误码!发送方此时,有可能发送的是0。如何让接收方,知道发送方发送的是1还是0呢?
因此,单个比特的符号无法传递1或0的信息!!!!这就需要通过增加冗余信息的编码,在出错率确定的情形下,使得即使传输过程中出错,接收方根据接收到的符号序列,也能够通过最大概率的方式猜出发送方最可能信息是1还是0!!!!
对于理想信道或无失真的信道,信道编码是没有任意意义的!!!
物理层编码的根本或罪为祸首是:信道是有干扰的信道,是有失真的信道。
如下图所示:
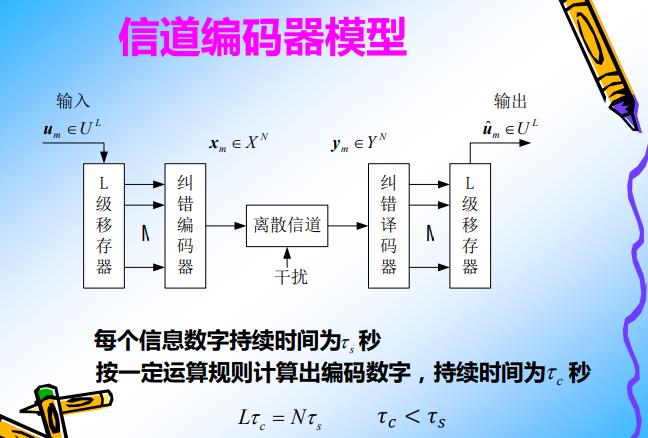
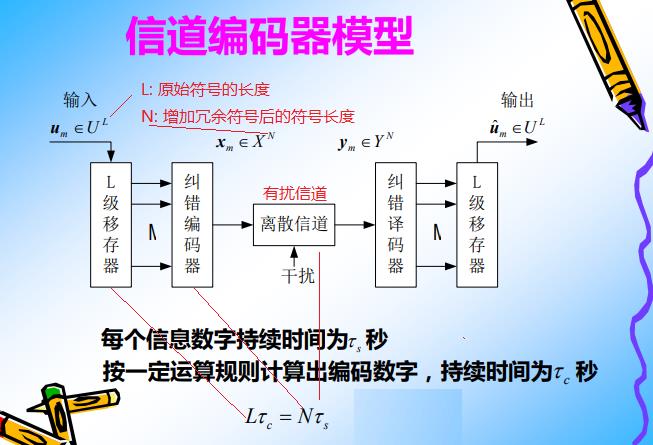

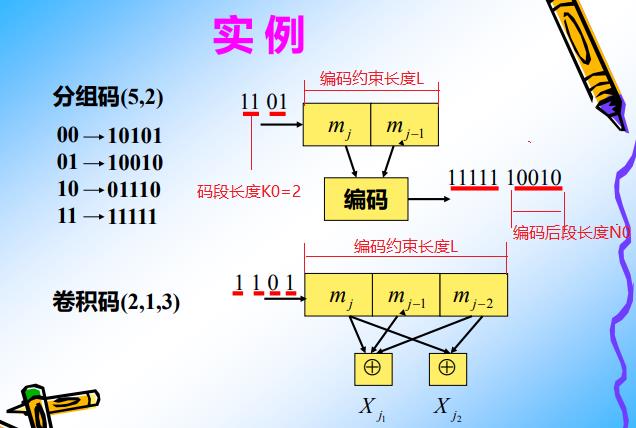

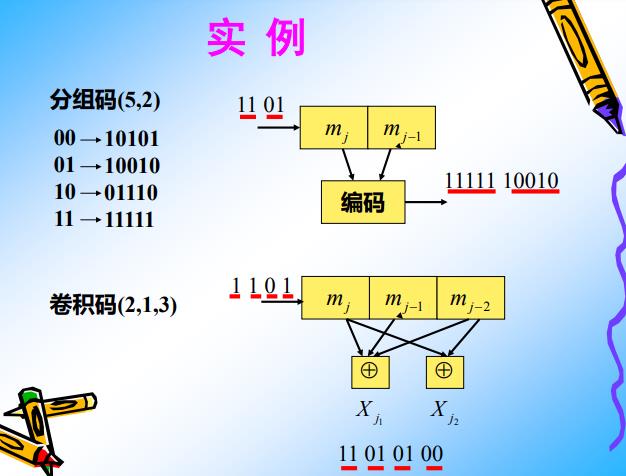
备注:
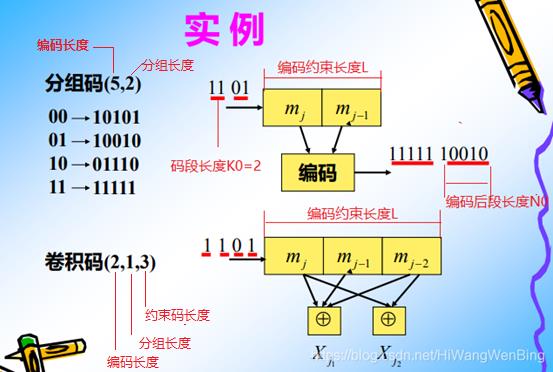
分组码:分组数(K0=2)与编码字符数(L=2) 相等,相邻两个码段时间没有依赖和关联关系.
卷积码:分组数(K0=1)与编码字符数(L32) 相等,相邻两个码段时间有依赖和关联关系.

备注:
- 编码率越高,表明有效比特符号比重越大,冗余符号比率越少,则纠错能力越弱。
- 编码率越低,表明有效比特符号比重越小,冗余符号比率越大,则纠错能力越强。
第2部分 信道的三种最佳译码准则

备注:
由于每个输入字符与输出字符之间的对应关系是一种概率事件 ,不是完全的1对1的关系。一个输入,可能有多个输出,一个输出,可能来源于多个不同的输入,根据输出,来反推(译码)成输入,就是一个概率事件,不是确切的事件。
译码准则就是在收到输出字符时,根据某种准则,把输出判断为某一个输入时的方法或准则。
如果该准则会导致整体的误码率是最低,这样的准则就是最优准则。
比如收到1101, 判断为01的概率是3/4, 判断为00的概率是1/4 那此时判断为什么呢?很显然判断为01是理想的选择。本文重点是确保通过某种译码选择,确保整体的误码率最低。
这就是本章节要讨论的问题。









第3部分 信道编码定理
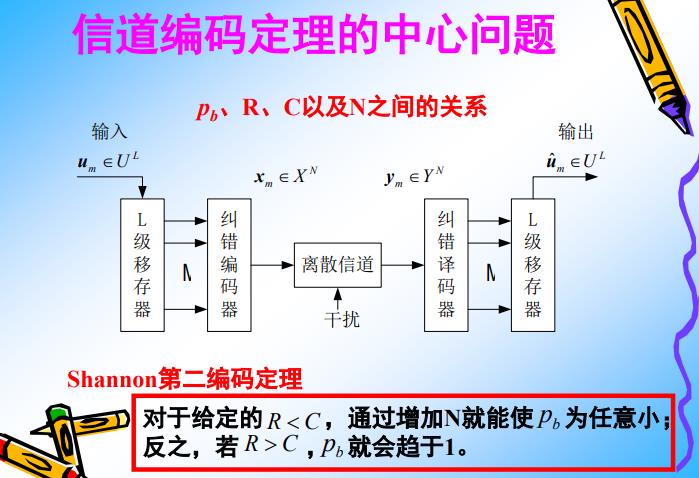
- Pb接收端的出错概率,也成出错率,这是有扰信道的必然结果
- R:发送速率
- C:信道容量,即可以承载的的最大速率
- N:物理层信道编码的长度
香农第二编码定理,就是研究上述4个参数的关系
信道编码定理:
(1)定理1:如果数据的发送速率小于信道容量,那么即使是有干扰信道,也总会通过增加冗余码的长度,总能找到一种物理层信道编码方案,可以使得接收端整体的出错率降到尽可能的小,接近于零。5G的POLAR和LDPC编码,就是这种方案。
(2)定理2:如果数据的发送速率大于信道容量,,即使信道是不干扰信道,也不可能存在某种编码方案(增加移动容易量)来确保信道的误码率无限接近0, 接近无失真信道。
或者,换成人话就是:对于一个任意物理信道,总能够找到一种方案,可以使得实际的信道传输速率达到此时信道的最大理论容量极限(香农极限)。5G POLAR和LDPC编码,就是一种能够使得物理层数据的传输的比特速率得到香农极限(由于具备纠错的能力,因此极大的降低了链路的误码率)
备注:该定理是通过增加冗余降低出错的概率,并没有涉及冗余后的编码效率问题。
实际上,增加的冗余越多,出错的概率越小,因此,在信噪比和出错概率确定的情况下,一定存在一种编码方法,使得增加的冗余是最小的,也就是编码效率是最高的!!!这就是物理层编码寻求的目标。
冗余信息的增加:降低出错概率的本质是对接收到的符号进行纠错,纠错的本质是选择概率最大,可能性最大的猜测,之所以猜测,是因为信道是有干扰的,收到的数据,并不一定就是发送的数据。如收到的符号是1,发送的符号并不一定是1,只是概率为1的可能性最大而已。

第4部分 分组码基本概念
4.1 分组码的基本概念


备注
编码方法与译码准则(解码准则)是成对出现的。就如调制与解调成对出现,发送与接收成对出现一样。


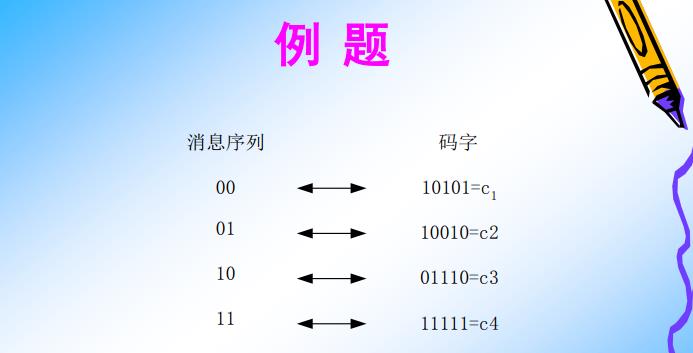
(1)信源码字
- 码元个数=2 (0或1)
- 码长L=2
- 码的个数:M = 2^2 = 4
(2)编码码字
- 码元q = 2 (0或1)
- 码长L=5
- 码的个数:N = 2^5 = 8个
- 许可码数目= M = 4个
- 禁止码数目 = N - M = 4个
- 编码效率R=L/M = 2/5 = 0.4 = 40%
备注:由于增加了冗余信息,信道编码后的码的长度肯定是大于原始码的长度的,且一定会存在多余的禁止码,这些多余的禁止码是多余的冗余码,可用来辅助检错与纠错。
编码后的码也有可能在传输过程中受干扰而出错,在接收有错误时,如何利用禁止码和许可码来判决或猜测发送端发送的是什么符号序列呢?有什么数学依据呢?

备注:
两个编码后的码序列的相似度,是通过对应位不相同的个数d来量化的。不相同的个数为0,则表示这两个码序列完全相同,如果不相同的个数为与码序列的长度相同,则表示所有比特位都不相同,是全异码。对应位不相同的个数d用一个专有名词表示:汉明距离!
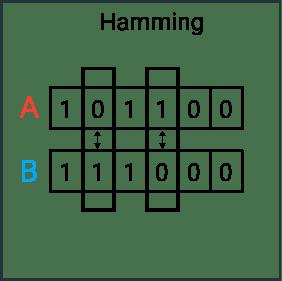
如0000与00000的汉明距离为0
如0000与11111的汉明距离为5
如0000与10101的汉明距离为3
如11111与10101的汉明距离为2
三维汉明空间:
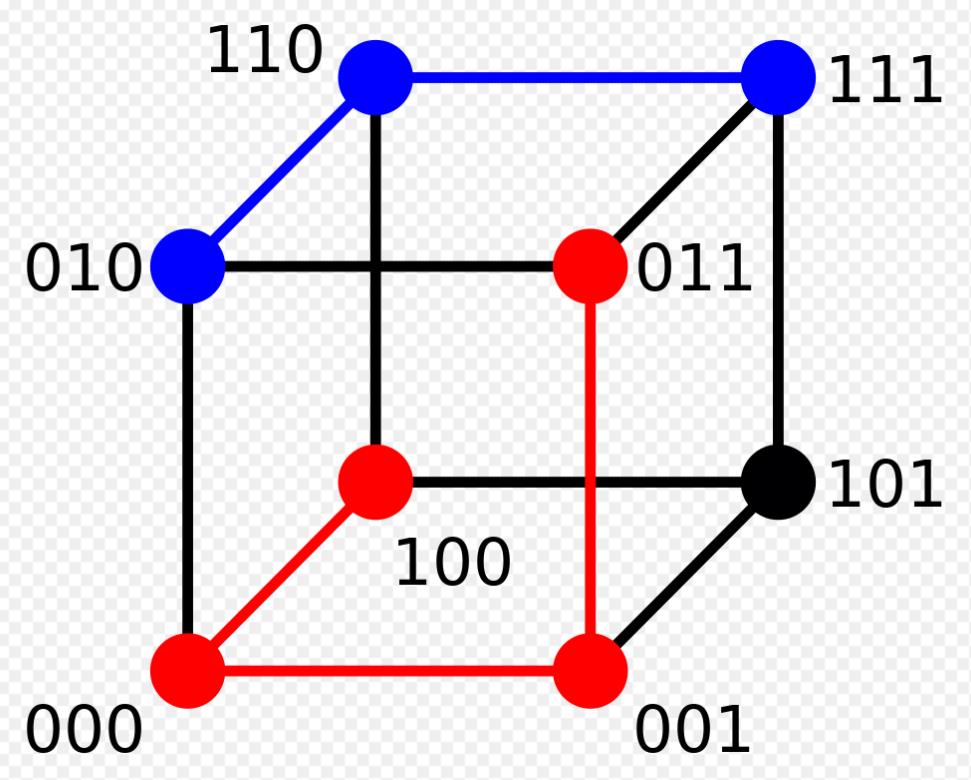
汉明距离:本质是两个码之间的最短边长的个数。
上述过程的数学表达为:

备注:
汉明距离是不同码元的个数(累计和)!!!!
计算机的计算方法:
(1)方法1:对因位亦或,然后相加,就得到了汉明距离d。
(1)方法2:两个比特序列先亦或得到一个新的序列,然后计算这个新序列中1的个数,即汉明重量,新序列的汉明重量w,就是汉明距离d。

汉明距离:描述了两个码之间的相似程度。
最小汉明距离:描述了一个码,错成另一个码的可能性,距离越小,说明两个码相似度越高,说明出错成另一个码的可能性越大。
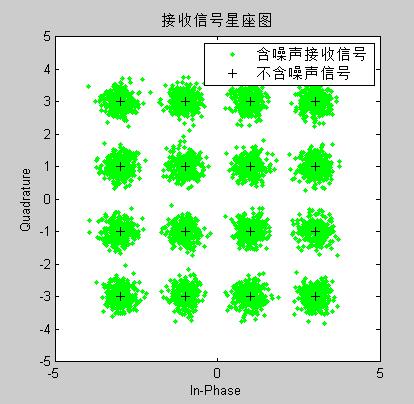

备注:任意两个码字之间的汉明距离中,最小的那个距离,表明那两个码字最相近。
4.2 最小汉明距离与检错、纠错能力的关系

备注:
两个独立码序列的最小汉明距离是1,为了提升两个独立码序列之间的抗干扰能力,就需要提升两个独立码序列之间的汉明距离。
提升两个独立码序列的汉明距离=》2
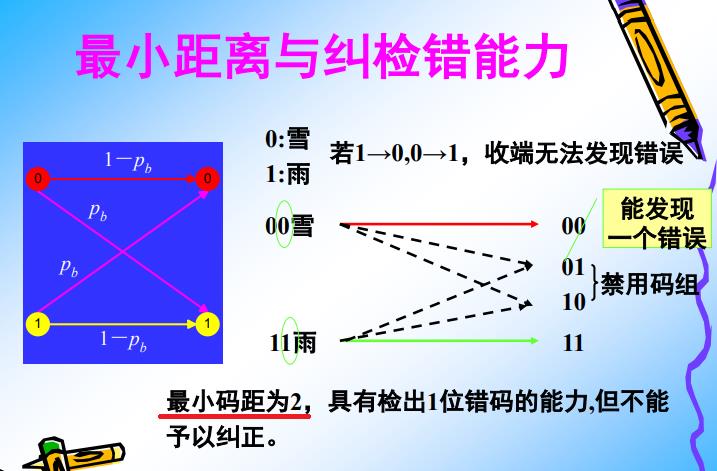
备注:
通过增加把两个独立序列的距离从1增加到2,提升了这两个独立码的抗干扰能力、提升了这两个独立码的检错能力(这个案例中,没有纠错的能力)
- 提升了抗干扰能力:必须同时有两个bit出错,接收端接收到的数据才是完全出错的。
- 提升了检错能力:当接收到01和10的时候,表明接收到的数据受干扰出错,但没有纠错能力,因为根据01或10,并不知道发送端是00还是11.
进一步提升两个独立码序列的汉明距离=》3
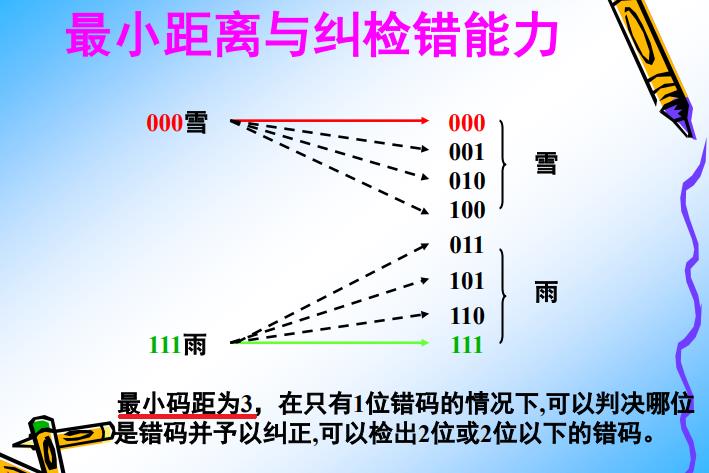
- 提升了抗干扰能力:必须同时有3个bits出错,接收端接收到的数据才是完全出错的。
- 具备2个bit同时出错的检错能力:当接收不是000和111的时候,表明接收到的数据受干扰出错,出现1或2个bit的出错。
- 具备1个bit同时出错的纠错能力:当出现1个bit出错的时候,如接收到001,就可以纠错成000,表明发送方发送的是“雪”; 如接收到110的时候,就可以纠错成111 -》1,表明发送方发送的是“雨”。
- 上述编码,不具备3个bit同时出错的检错和纠错能力。
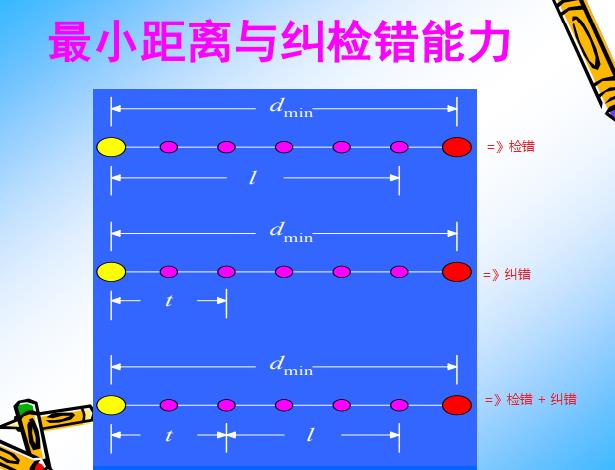
汉明距离的纠错能力、纠错能力的数学表达式:

备注:
上图中的l,t都是同时出错的比特数。不过一个是检错,一个是纠错。
很显然,纠错的能力对汉明距离的要求比检错能力对汉明距离的要求大很多。
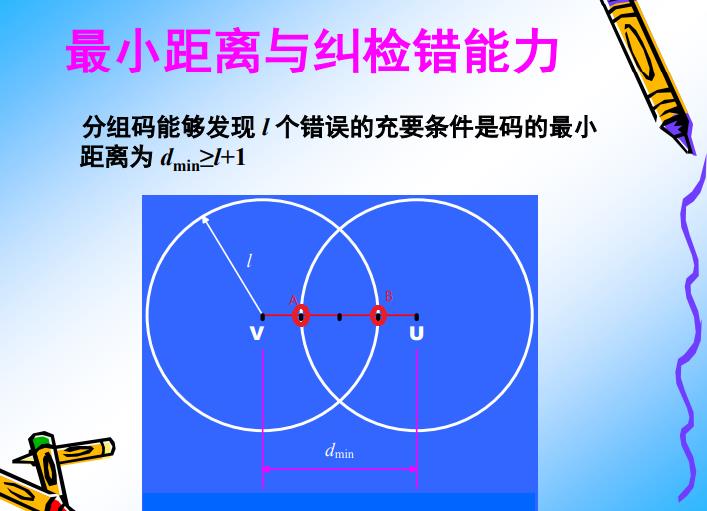
备注:
- 当接收到的序列,在圆心时,表示没有任何比特出错,为v或u。
- 当接收到的序列,不是圆心时,而是在圆周或圆内时,表示传输出错,因此具备了检错能力。
- 当接收到的序列,不是圆心时,而是在圆周或圆内时,可以判别为圆心,则局部了一定的纠错能力。
- 当接收到的序列,不是圆心时,而是在两个圆相交处时,就无法判断。只能纠错,无法检错。
- 当dmin = l时,会导致V的圆心与u的圆周重叠,反之亦然,这就导致“误判”,误判的结果就是接收端接收了一个错误的数据,而不是自知,这是不可接受的。因此必须要求dmin > L
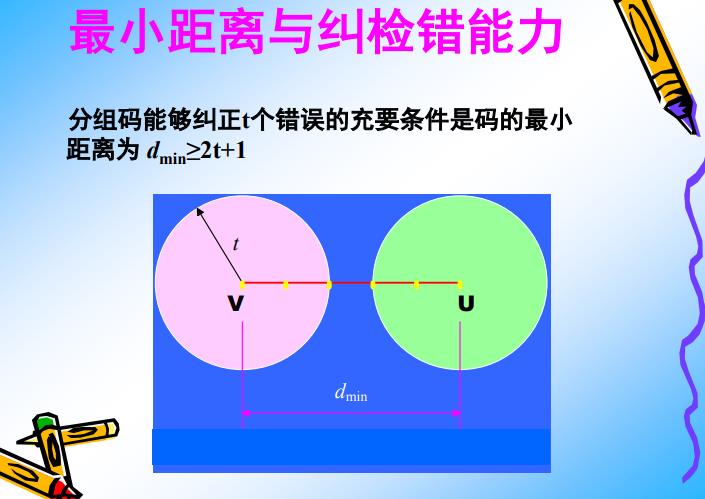
备注:
- v的半径是t
- u的半径是t
- Dmin >= 2t + 1表明这两个圆不会相交,任何t位出错的码,要么落在v的圆内,要么落在u的圆内,都可以被判为v或u,这就具备了完全的纠错能力。
- 纠错位数t越大,圆的半径越大,面积越大,汉明距离Dmin要求就越大,这要求的冗余码就越多。
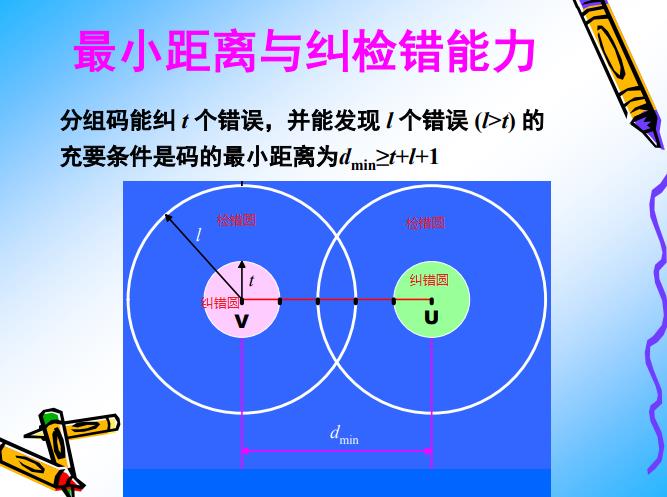
备注:
上述同时具备一定的纠错能力和检错能力的公式的解释如下:
- v和u的纠错圆不能相交
- v和u的检错圆可以相交
- 检圆比纠错圆的半径要大,也就是纠错的汉明距离要求高于检错的汉明距离。
- v检错圆与u的纠错圆不能相交
- u检错圆与v的纠错圆不能相交


第5部分 线性分组码的代数基础
第6章 线性分组码

分组码:
将信源的信息序列分成独立的块进行处理和编码,称为分组码。编码时将每k个信息位分为一组进行独立处理,变换成长度为n(n>k)的二进制码组。此时的编码效率为n/k。
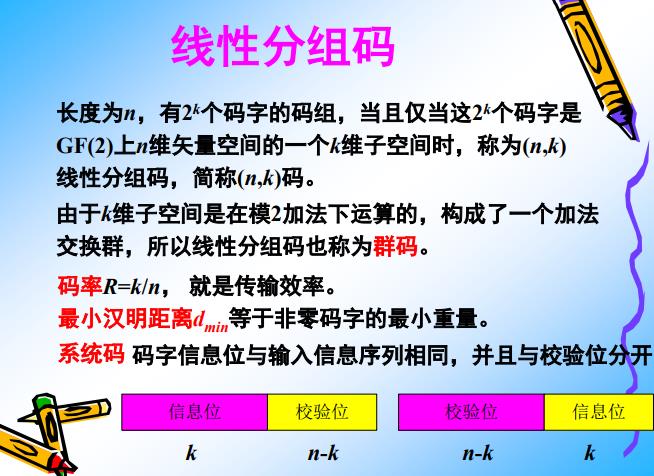
线性分组码:
一个[n,k]线性分组码,是把信息划成k个码元为一段(称为信息组),通过编码器变成长度为n个码元的一组,作为[n,k]线性分组码的一个码字。
若每位码元的取值有q种(q为素数幂,q进制),则共有q的k次方个码字。二进制码元就是一种q=2的线性分组码。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/118638025
视频:https://www.icourse163.org/course/XDU-1002199004?tid=1450252482
以上是关于[信息论与编码理论专题-6]:物理层信道编码的主要内容,如果未能解决你的问题,请参考以下文章
《信息与编码》考试复习笔记6----第六章连续信源熵和信道容量(考点在连续信道容量)
MATLAB教程案例9信道编译码之turbo编码译码算法matlab误码率仿真