积分级数题集02
Posted 梧桐鹿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了积分级数题集02相关的知识,希望对你有一定的参考价值。
\\[I_k = \\int_0^\\infty e^{-nx} \\sin^{2k}\\! x {\\rm d}x \\quad(n,k\\in \\mathbb{N}^*) \\]
Solution:
\\[\\begin{align*}
I_k &= \\int_0^\\infty e^{-nx} \\sin^{2k}\\! x {\\rm d}x \\\\
&=\\left[-\\frac{1}{n}e^{-n x}\\sin^{2k}\\! x\\right]_0^\\infty-\\int_0^\\infty -\\frac{2k}{n}e^{-nx} \\sin^{2k-1}\\! x \\cos x{\\rm d}x \\\\
&=\\frac{2k}{n} \\int_0^\\infty e^{-n x}\\sin^{2k-1}\\!x\\cos x{\\rm d}x \\\\
&=\\frac{2k}{n}\\left(\\left[-\\frac{1}{n}e^{-n x}\\sin^{2k-1}\\!x\\cos x\\right]_0^\\infty-\\int_0^\\infty -\\frac{1}{n}e^{-n x}\\frac{{\\rm d}}{{\\rm d}x}(\\sin^{2k-1}\\!x\\cos x){\\rm d}x \\right) \\\\
&=\\frac{2k}{n^2}\\int_0^\\infty e^{-n x}\\left((2k-1)\\sin^{2k-2}\\!x \\cos^2 x-\\sin^{2k}\\!x\\right){\\rm d}x \\\\
&=\\frac{2k}{n^2}\\int_0^\\infty e^{-n x}\\left((2k-1)\\sin^{2k-2}\\!x (1-\\sin^2 x)-\\sin^{2k}\\!x\\right){\\rm d}x \\\\
&=\\frac{2k}{n^2}\\int_0^\\infty e^{-n x}\\left((2k-1)\\sin^{2k-2}\\!x-2k\\sin^{2k}\\!x\\right){\\rm d}x \\\\
&=\\frac{2k\\times(2k-1)}{n^2}I_{k-1}-\\frac{2k \\times2k}{n^2}I_{k}\\\\
n^2 I_k &= 2k(2k-1)I_{k-1}-4k^2I_k \\\\
(n^2+4k^2)I_k&=2k(2k-1)I_{k-1} \\\\
I_k &= \\frac{2k(2k-1)}{n^2+4k^2} I_{k-1}
\\end{align*}
\\]
接下来只需求出 \\(I_0\\) 即可
\\[I_0 = \\int_0^\\infty e^{-nx}{\\rm d}x= \\left[-\\frac{1}{n}e^{-nx}\\right]_0^\\infty
= \\frac{1}{n}
\\]
经过简单递推容易得到
\\[I_k = \\frac{(2k)!}{n \\prod_{j=1}^k (n^2 + 4j^2)}
\\]
\\(\\square\\)
以上是关于积分级数题集02的主要内容,如果未能解决你的问题,请参考以下文章
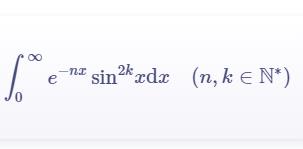 ╰(*°▽°*)╯
╰(*°▽°*)╯