动态滴定预测算法研究

Posted 2021-08-06 卓晴

简 介： 对于取得的滴定数据使用了单位滴定面积倒数预测剩余水量模型进行预测，渴望获得比较好的预测精度，最后给出了进一步实验的步骤和方向。

关键词： 动态滴定预测研究，卡式水分滴定

 

§01 卡式水分滴定

---

一、滴定过程加速

  在卡式水分滴定过程的采集采用了 不同采集方案精度对比 ，并在此基础上对于 卡尔费休滴定进行建模 ，所有的目的是为了能够加快滴定过程。

  在上次在先驱威锋讨论的时候对于整个滴定过程分为了三部分：

• 滴定起始阶段：此时滴定杯中存有大量的水，远离平衡态；此时稳态电流检测值基本上为0.
• 终点过度阶段：此时稳态电流在5 ~ 20 微安左右。
• 终点平衡阶段：此时稳态电流在20 至28微安左右，逐步靠近滴定终点。

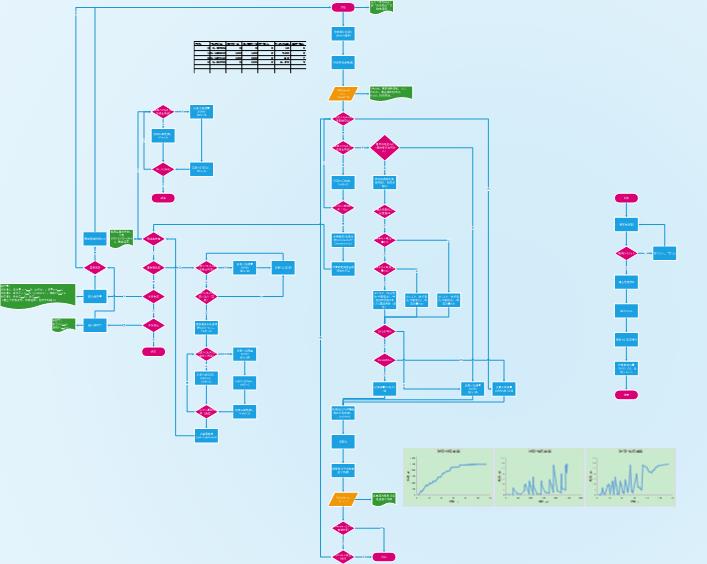
▲ 图1.1 卡式水分滴定流程图

  按照上面的动态滴定框图可以大大提高第二阶段（过渡过程）。

  下面则需要分别针对起始阶段以及平衡阶段的响应的控制算法进行研究。

 

§02 数据分析

---

一、原始数据文件

1、刘通发送EXCEL数据

  下面四个原始数据文件是由刘通发送过来：

• 2021-07-05 上午50mL反应体积.xlsx
• 2021-07-05 下午100mL反应体积.xlsx
• 20210703-预测卡氏液消耗量.xlsx
• 20210705-预测卡氏液消耗总量.xlsx

D:\\zhuoqing\\DesignCenter\\XQWF\\2021\\水分滴定

2、TEXT数据

  以下是四月份的测量数据。其中包括有加入的测试水分，每步增加的卡式液的体积等不同的组合。

（1）实验参数组合

【表1-1 实验不同的参数组合】

水：μL	0.5	1	2	5	10	15
卡氏液uL	1000	200	400	1000	2000	3000
1000 μL	不测	不测	不测	不测	-	-
500 μL	不测	不测	不测	-	-	-
250 μL	不测	不测	-	-	-	-
100 μL	不测	-	-	-	-	-
50 μL	-	-	-	-	-	-

（2）实验测量数据文件

1. KS-转速240-加水量0.5-滴定度5.443-加液速度20-溶剂总体积50-单步馈液50-01.txt
2. KS-转速240-加水量1-滴定度5.443-加液速度20-溶剂总体积70-单步馈液50-01.txt
3. KS-转速240-加水量1-滴定度5.443-加液速度20-溶剂总体积70-单步馈液100-01.txt
4. KS-转速240-加水量2-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液50-01.txt
5. KS-转速240-加水量2-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液100-01.txt
6. KS-转速240-加水量2-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液250-01.txt
7. KS-转速240-加水量5-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液50-01.txt
8. KS-转速240-加水量5-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液100-01.txt
9. KS-转速240-加水量5-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液250-01.txt
10. KS-转速240-加水量5-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液500-01.txt
11. KS-转速240-加水量10-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液50-01.txt
12. KS-转速240-加水量10-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液100-01.txt
13. KS-转速240-加水量10-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液250-01.txt
14. KS-转速240-加水量10-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液500-01.txt
15. KS-转速240-加水量10-滴定度5.443-馈液速度20-溶剂总体积70-单步馈液1000-01.txt
16. KS-转速300-加水量15-滴定度5.443-馈液速度20-溶剂总体积100-单步馈液50-01.txt
17. KS-转速300-加水量15-滴定度5.443-馈液速度20-溶剂总体积100-单步馈液100-01.txt
18. KS-转速300-加水量15-滴定度5.443-馈液速度20-溶剂总体积100-单步馈液250-01.txt
19. KS-转速300-加水量15-滴定度5.443-馈液速度20-溶剂总体积100-单步馈液500-01.txt
20. KS-转速300-加水量15-滴定度5.443-馈液速度20-溶剂总体积100-单步馈液1000-01.txt

（3）实验数据格式

  实验条件和数据分别反映在实验数据文件名称与数据格式中。

• 实验舒适名称中的信息可以只有通过文件名称的不同字段来反映；
• 实验数据文件包括有若干行：每一行的组成如下表所示：

【表1-2 滴定数据每一行格式】

数字1	数字2	数字3	数字4-n
滴定步数 从1开始，到文件结束递增	剩余的水量：μL	滴定液量：μL	电流值数量 10秒钟的数据,总共150个记录数据

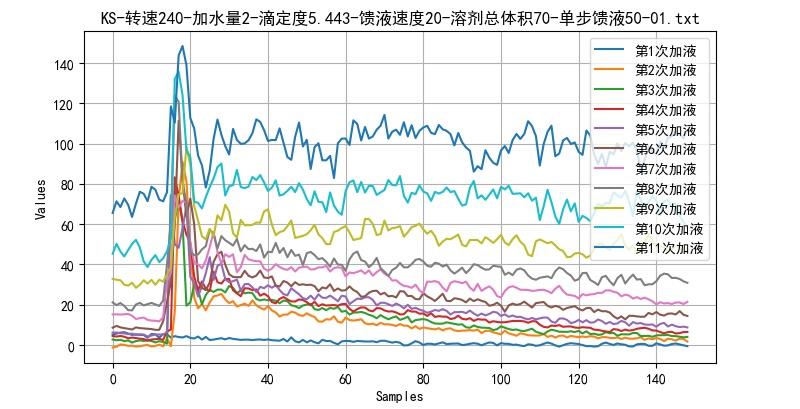
▲图2.1 一次滴定过程中的数据

dirpath = tspstring2text('datadir')
#printf(dirpath)
filedim = os.listdir(dirpath)
#printf(filedim)
def arg2file(water, karl):
    for f in filedim:
        if f.find('加水量%s'%water) > 0 and f.find('单步馈液%s'%karl) > 0:
            return os.path.join(dirpath, f)
    return 'NO FILE'
#------------------------------------------------------------
filename = arg2file(2, 50)
printf(filename)
with open(filename, 'r', encoding='gbk') as f:
    lines = f.readlines()
    printf(len(lines))
    count = 0
    for s in lines:
        count += 1
        sdim = [float(sn) for sn in s.split() if len(sn) > 0]
        plt.plot(sdim[4:], label='第%d次加液'%count)
plt.title(os.path.basename(filename))
plt.xlabel("Samples")
plt.ylabel("Values")
plt.legend(loc='upper right')
plt.grid(True)
plt.tight_layout()
plt.show()

二、数据分析

1、滴定电流积分

  分析滴定电流积分（面积）与滴定液之间的变化关系。

（1）加水量2-单步馈液50

  这次滴定曲线为上面【图2.1】所示。可以看到第一次滴液的时候电流值并没有发生变化，所以这次滴液忽略。积分数值选择从第10 个开始到底55个结束，大约经过三秒钟的时间。

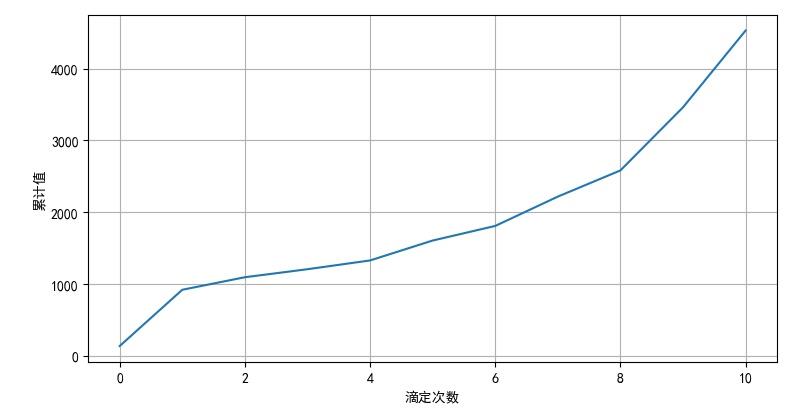
▲ 图2.1 11次滴定面积

  去掉第一个，将其余的取倒数：

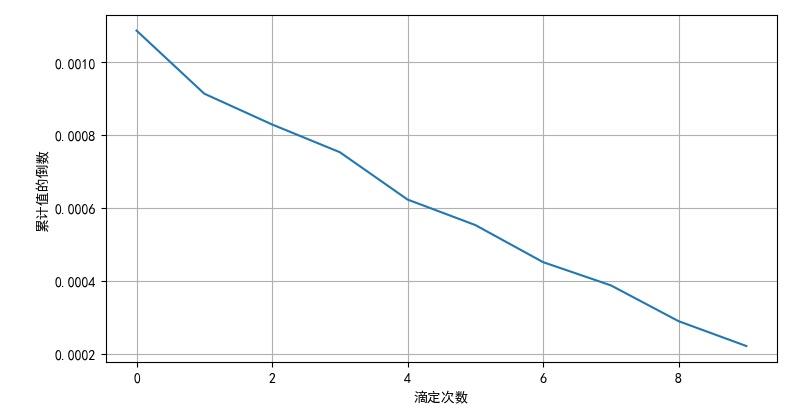
▲ 图2.2 从第二次滴定到最后一次滴定的倒数数值

（2）加水量5-馈液量50

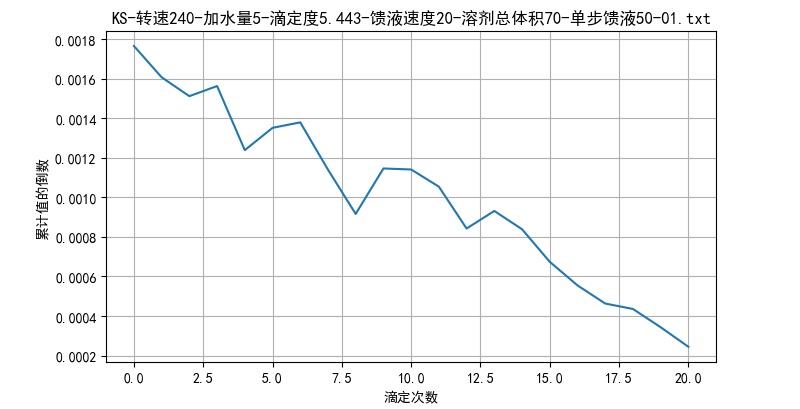
▲ 图2.3 加水量5-馈液量50

  上面的面积计算采用了三秒的数据积分，下面采用8秒时间的积分，计算出面积倒数与滴定次数之间的关系。

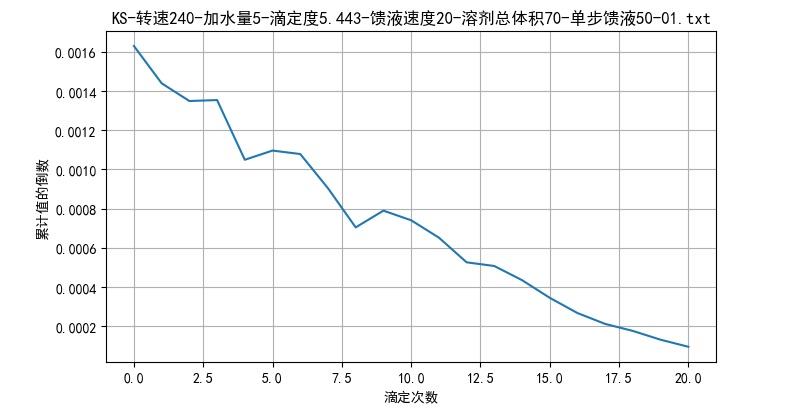
▲ 图2.4 8秒时间的积分得到的面积倒数与滴定次数之间的关系

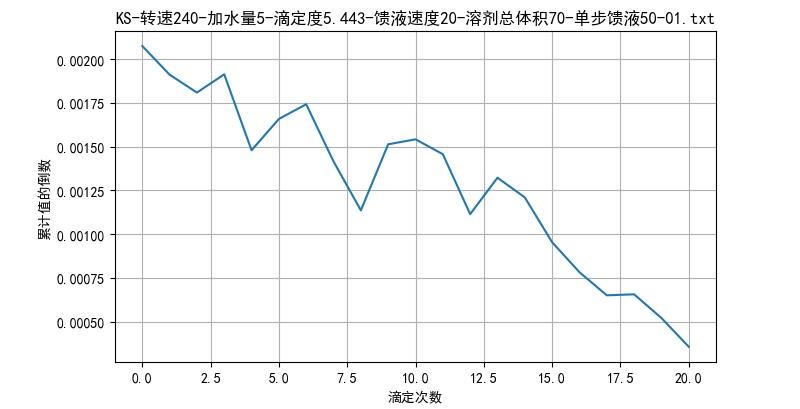
▲ 图2.5 两秒时间的面积积分与滴定次数之间的关系

  下面对于不同的积分时间下积分面积的倒数与滴定次数之间的关系：

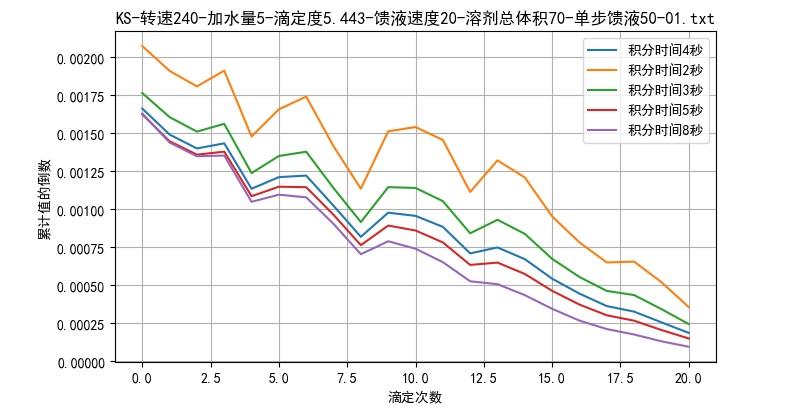
▲ 图2.6 不同的积分时间对于计算关系的影响

  积分时间越长，上述面积的导数与滴定步数之间的线性关系越好。在数据的稳定性与时间之间做平衡，在后面的实验中，积分时间取5秒。

  由于滴定是采用了等间隔滴定，所以剩余水分随着滴定次数线性下降。因此从前面滴定曲线来看，每次滴定的面积倒数与剩余水量之间大体呈现正比的关系。

2、全部实验

  下面对于前面实验的输出做统一的处理。得到第一滴滴定积分面积的导数与剩余水量之间的关系。处理数据的相关参数：

• 从数据名称得到加水量，也就是对应的溶液中的水量；
• 从数据名称中得到滴定水量：也就是馈液量；
• 分别计算数据的第一条积分面积和第二条积分面积；
• 积分数据从10 ~ 10+75，供5秒的数据；

（1）处理程序

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST3.PY                     -- by Dr. ZhuoQing 2021-07-08
#
# Note:
#============================================================

from headm import *

dirpath = tspstring2text('datadir')
filedim = os.listdir(dirpath)

def arg2file(water, karl):
    for f in filedim:
        if f.find('加水量%s'%water) > 0 and f.find('单步馈液%s'%karl) > 0:
            return os.path.join(dirpath, f)

    return 'NO FILE'
#------------------------------------------------------------

def filearg(filename):
    with open(os.path.join(dirpath, filename), 'r', encoding='gbk') as f:
        lines = f.readlines()

        line1 = lines[0]
        line2 = lines[1]

        data1 = [float(s) for s in line1.split() if len(s) > 0]
        data2 = [float(s) for s in line2.split() if len(s) > 0]

        area1 = sum(data1[10:85])
        area2 = sum(data2[10:85])

        files = filename.split('-')
        printf(files)

        return (area1, area2,
                float(files[1][2:]),
                float(files[2][3:]),
                float(files[3][3:]),
                float(files[4][4:]),
                float(files[5][5:]),
                float(files[6][4]))

datadim = []
for f in filedim:
    d = filearg(f)
    datadim.append(d)

tspsave('dataall', data=datadim)

#------------------------------------------------------------
#        END OF FILE : TEST3.PY
#============================================================

（2）二十个文件处理结果

  下面是对二十个数据文件处理的结果。可以看到所有文件的第一个数值都小于第二个数值，特别是第一个滴定数值有的甚至为复数，这说明使用第二个滴定曲线的面积更为准确。这与前面的实验结果是相同的。

【表2-1 二十个文件滴定面积积分】

序号	面积2	转速	加水量	体积	单步馈液
0	2618.78	240.00	0.50	50.00	50.00
1	4197.93	240.00	1.00	70.00	100.00
2	2060.49	240.00	1.00	70.00	50.00
3	658.96	240.00	10.00	70.00	100.00
4	5542.40	240.00	10.00	70.00	1000.00
5	1770.17	240.00	10.00	70.00	250.00
6	234.24	240.00	10.00	70.00	50.00
7	3158.55	240.00	10.00	70.00	500.00
8	2631.48	240.00	2.00	70.00	100.00
9	7010.46	240.00	2.00	70.00	250.00
10	1211.81	240.00	2.00	70.00	50.00
11	1299.90	240.00	5.00	70.00	100.00
12	3504.06	240.00	5.00	70.00	250.00
13	612.20	240.00	5.00	70.00	50.00
14	7008.82	240.00	5.00	70.00	500.00
15	264.14	300.00	15.00	100.00	100.00
16	2069.19	300.00	15.00	100.00	1000.00
17	669.59	300.00	15.00	100.00	250.00
18	134.68	300.00	15.00	100.00	50.00
19	1280.25	300.00	15.00	100.00	500.00

data = tspload('dataall', 'data')

printf("序号 面积2 转速 加水量 体积 单步馈液")
for id,d in enumerate(data):

    printf("%d %5.2f %5.2f %5.2f %5.2f %5.2f"%(id, d[1], d[2], d[3], d[6], d[7]))

3、多元回归分析

  在【表格2-1】中，通过面积2，转速、体积、单步馈液来回归加水量。下面定义相关变量名：

定义相关变量名：

加水量： $W$
面积： $A$
转速： $R$
体积： $V$
馈液量： $S$

（1）单位滴定面积倒数关系

  根据之前讨论的结果，一种最基本的猜测是利用面积A的倒数来预测加水量A。由于面积与单步馈液量之间存在正向关系，所以下面使用 $A/S$来线性预测W数值，这个预算成为单位滴定面积预测。

【表2-3 利用单位滴定面积倒数预测加水量】

序号	S/A	S	W	W*A/S
0	0.02	50.00	0.50	26.19
1	0.02	100.00	1.00	41.98
2	0.02	50.00	1.00	41.21
3	0.15	100.00	10.00	65.90
4	0.18	1000.00	10.00	55.42
5	0.14	250.00	10.00	70.81
6	0.21	50.00	10.00	46.85
7	0.16	500.00	10.00	63.17
8	0.04	100.00	2.00	52.63
9	0.04	250.00	2.00	56.08
10	0.04	50.00	2.00	48.47
11	0.08	100.00	5.00	64.99
12	0.07	250.00	5.00	70.08
13	0.08	50.00	5.00	61.22
14	0.07	500.00	5.00	70.09
15	0.38	100.00	15.00	39.62
16	0.48	1000.00	15.00	31.04
17	0.37	250.00	15.00	40.18
18	0.37	50.00	15.00	40.40
19	0.39	500.00	15.00	38.41

  从上述实验中，可以看到一个W/(S/A)的数值在40左右呈现比较多的次数。经过归纳，可以看到如下规律：

• 单步滴定在50μL；
• 加水量在15微升

  下面是将上面表格中符合的条件摘录下来，可以看到除了W= 0.5， W= 5之外其它都差不多在40左右。

序号	S/A	S	W	W*A/S
0	0.02	50.00	0.50	26.19
2	0.02	50.00	1.00	41.21
6	0.21	50.00	10.00	46.85
10	0.04	50.00	2.00	48.47
13	0.08	50.00	5.00	61.22
15	0.38	100.00	15.00	39.62
16	0.48	1000.00	15.00	31.04
17	0.37	250.00	15.00	40.18
18	0.37	50.00	15.00	40.40
19	0.39	500.00	15.00	38.41

（2）处理4月8日数据

  下面时对于4月8日的数据进行处理。可以看到单位滴定积分面积导数与加水量之间的比值发生了变化。不过仍然有很多的曲线符合这个关系。

序号	S/A	S	W	W*A/S
0	0.02	50.00	0.50	26.70
1	0.02	100.00	1.00	46.19
2	0.03	50.00	1.00	35.30
3	0.37	100.00	10.00	26.85
4	0.30	1000.00	10.00	33.89
5	0.28	250.00	10.00	36.21
6	0.39	50.00	10.00	25.61
7	0.26	500.00	10.00	39.13
8	0.04	100.00	2.00	53.53
9	0.04	250.00	2.00	49.25
10	0.05	50.00	2.00	42.08
11	0.12	100.00	5.00	41.08
12	0.10	250.00	5.00	52.09
13	0.14	50.00	5.00	36.81
14	0.09	500.00	5.00	53.03
15	0.82	100.00	15.00	18.39
16	0.59	1000.00	15.00	25.40
17	0.64	250.00	15.00	23.26
18	0.88	50.00	15.00	17.02
19	0.59	500.00	15.00	25.57

（4）使用第三滴面积预测

  下面使用第三滴单位面积进行预测。可以看到在每一滴为50微升的时候吧，也会得到40左右的预测比例系数。

序号	S/A	S	W	W*A/S
0	0.01	50.00	0.50	42.89
1	0.02	100.00	1.00	60.32
2	0.02	50.00	1.00	51.49
3	0.16	100.00	10.00	61.32
4	0.11	1000.00	10.00	92.66
5	0.12	250.00	10.00	82.65
6	0.22	50.00	10.00	44.70
7	0.10	500.00	10.00	96.90
8	0.03	100.00	2.00	76.53
9	0.02	250.00	2.00	91.80
10	0.03	50.00	2.00	60.21
11	0.06	100.00	5.00	80.54
12	0.05	250.00	5.00	96.14
13	0.07	50.00	5.00	68.59
14	0.05	500.00	5.00	109.24
15	0.36	100.00	15.00	41.21
16	0.29	1000.00	15.00	52.52
17	0.34	250.00	15.00	43.68
18	0.39	50.00	15.00	38.01
19	0.28	500.00	15.00	53.32

 

§03 分析结论

---

一、分析结论

  通过前面的分析，大体可以的到如下的结论：

  1. 利用滴定曲线的积分面积的倒数预测剩余水量具有一定的实验基础；
  2. 通过对比不同时间的积分面积，可以大体看到使用3 ~ 5秒中采集的数据积分比较合适。
  3. 对于转速在预测中的影响，由于数据比较少，所以还无法得到进一步的验证。
  4. 在滴定度为5.44左右的时候，S/A预测W的系数大体为40左右；
  5. 前两滴的体积最佳方案为50 ~ 100。

二、补充实验

1、不同水量的滴定

  采用以下滴定条件，做不同水量下的滴定曲线：

• 转速：300r/s

• 单步馈液：50uL

• 滴定度：保持恒定

• 采样时间：6秒钟；

• 加水量分别为： 0.5，1，2，5,10, 12，15，18， 20，25

2、不同转速的滴定

  在转速为240,260,280,300， 加水量为5微升的情况下，单步馈液量仍然是5微升，进行滴定。

  为了加快实验，由于只需要获得前三次滴定曲线，因此。从第四步开始，就可以根据已知的加水量，增大单步滴定，尽快达到平衡，从而进行下一次时间。

3、实验目的：

• 进一步确认上述预测模型的准确性；
• 获得最佳的转速设置；
• 根据多次测量的结果，能够建立起 第二滴曲线面积，第三滴曲线面积与加水量的回归模型。

三、新的算法模型

通过前面的实验，可以确定一个比较安全的单位滴定曲线面积倒数$1/A$与剩余水量$W$之间的比率。然后再根据滴定度，确定预加滴定液体积$V$。

因此，滴定的起始阶段可以按照下面步骤进行：

无人机数字孪生算法研究

动态规划下的维特比算法在词性预测上的应用

基于遗传算法的BP神经网络在汇率预测中的应用研究（Matlab代码实现）

数字金融与算法研究（十九）—基于BP神经网络的股价预测

Python | 基于LendingClub数据的分类预测研究Part01——问题重述+特征选择+算法对比